【Machine Learning】8 神经网络：表述（Neural Networks:Representation）

最新推荐文章于 2025-04-28 22:46:59 发布
原创 最新推荐文章于 2025-04-28 22:46:59 发布 · 322 阅读 · 1 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#Machine Learning

本文深入探讨了神经网络的基本结构和工作原理，包括非线性假设处理、模型表示、前向传播过程，以及如何通过多层神经元实现复杂的非线性函数。通过具体例子，如逻辑门和XNOR门的实现，展示了神经网络学习非线性假设的能力。此外，还讨论了神经网络在多类分类任务中的应用。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

8.1 非线性假设（Non-linear hypotheses）

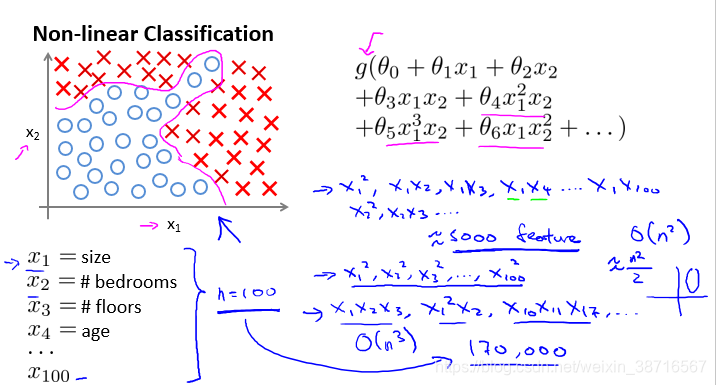
在非线性的多项式中，特征数变多，特征耦合产生的项数目庞大，普通的逻辑回归根本无法处理此类问题。

8.2 神经元和大脑（Neurons and the brain）

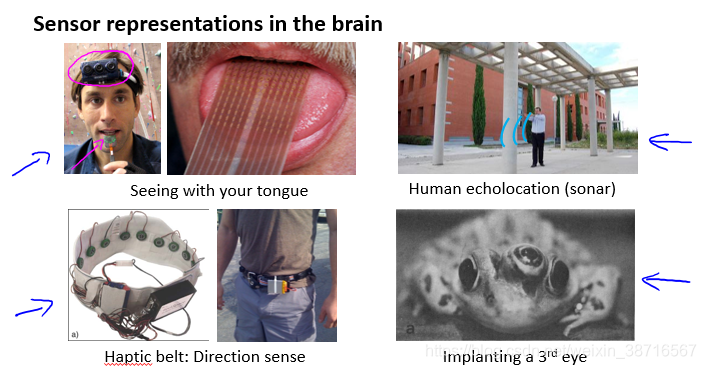
大脑学习的方法与计算机的算法

8.3 模型表示 I（Model representation I）

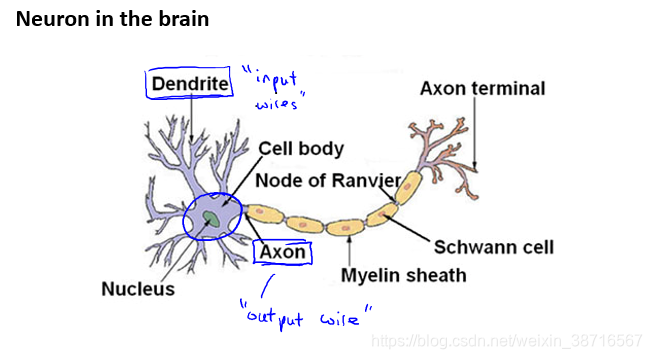
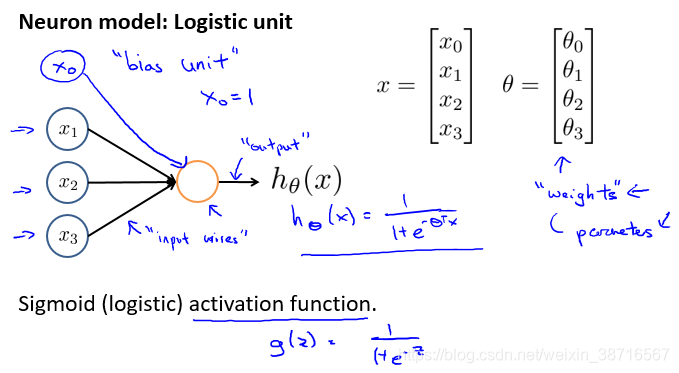
神经网络示意如上图。

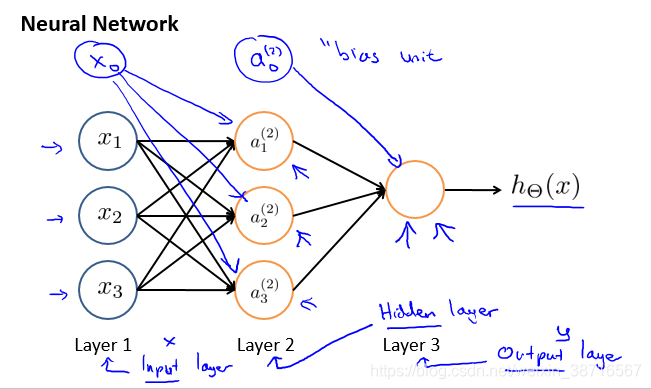
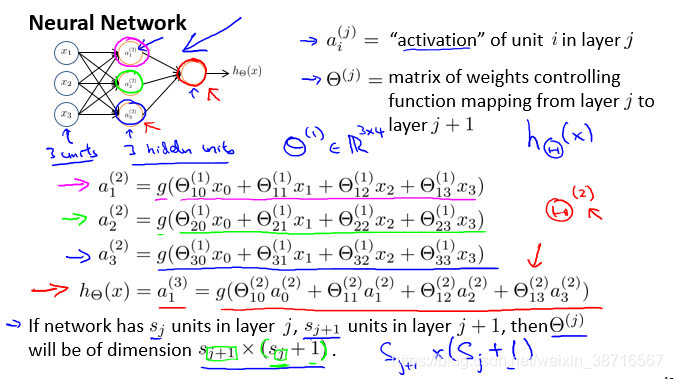
神经网络基本结构及其详解。

8.4 模型表示 II（Model representation II）

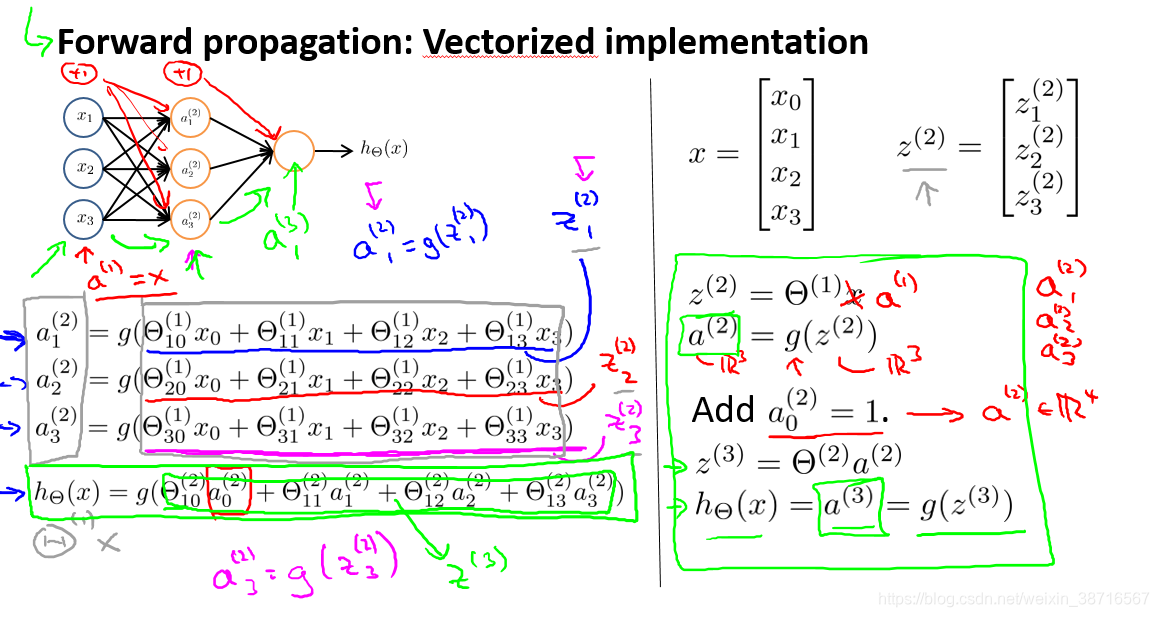
前向传播示意图，如图右半部分所示，可以表示为矩阵 向量乘积。

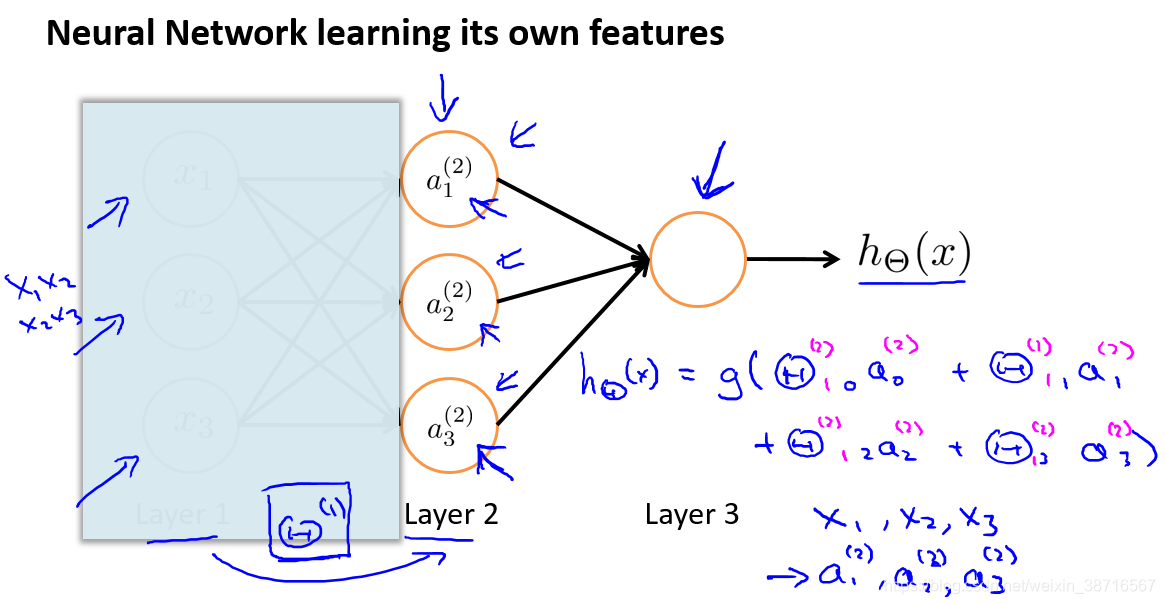
  把左边部分挡住，这可以看作一个逻辑回归，但这里的输入不再是x，而是a。不过a也是在x中学习得到的，可以看作比x更高级更复杂也更有效的特征，为什么会更有效或者高阶特征如何利用 ？往下\downarrow

8.5 例子和直观理解（Examples and intuitions I）

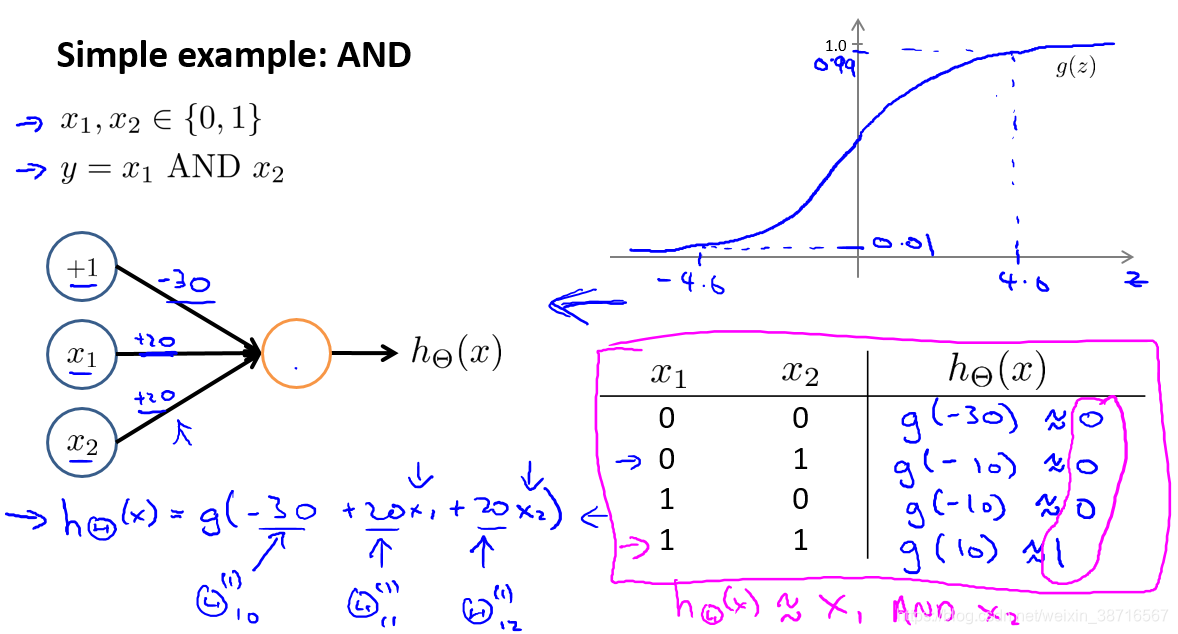
通过一个具体的神经网络求解输入为非线性函数的例子让我们理解神经网络如何学习非线性假设。

加入一个偏置单元

简单的神经元实现AND逻辑门：                                            简单神经元实现OR逻辑门：

  

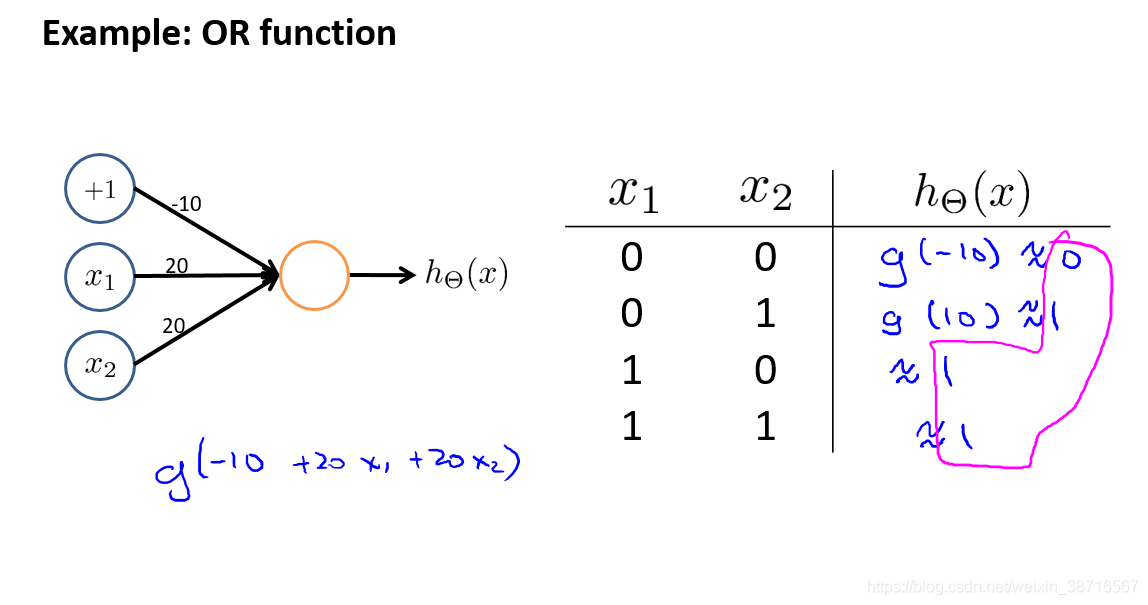
简单神经元实现NOT逻辑门：

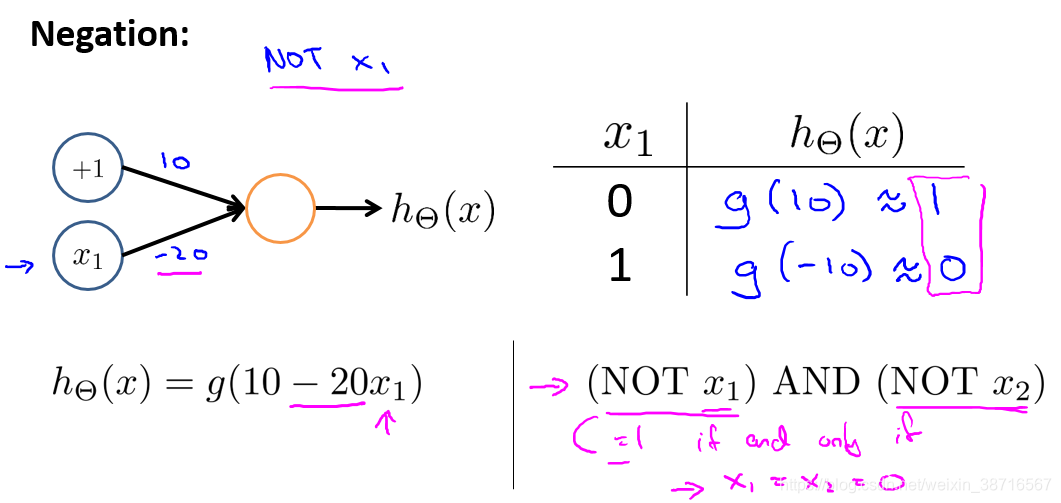
8.6 例子和直观理解（Examples and intuitions II）

我们想要实现一个同或门XNOR，需要在I中基本逻辑门上建立神经网络：

已知xnor=(x_{1}\,and\,x_{2})or(not\,x_{1}\,and\,not\,x_{2})

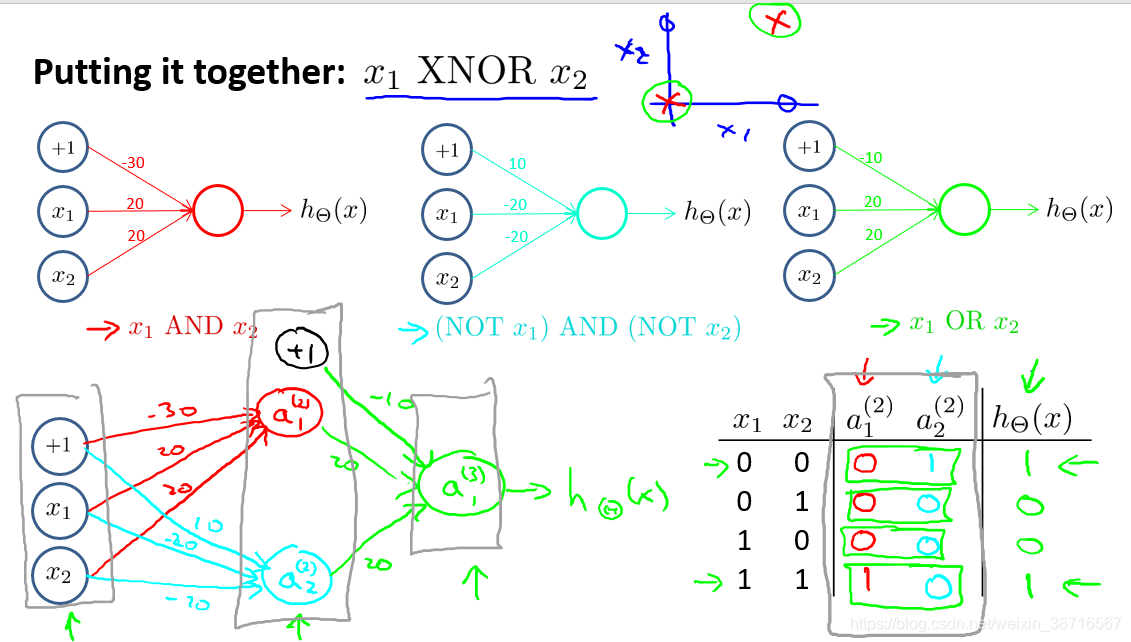
通过多个隐藏层，我们可以实现更复杂的函数，这就是神经网络这种结构的好处。

输入的特征\rightarrow复杂的特征\rightarrow更复杂的特征\rightarrow\cdots\rightarrow想要的结果

8.7 多类分类

我们需要训练神经网络，得到如下四个输出，来帮助我们分类行人、汽车、摩托、卡车。

值得注意的是这里的输出不用{1，2，3，4}表示。

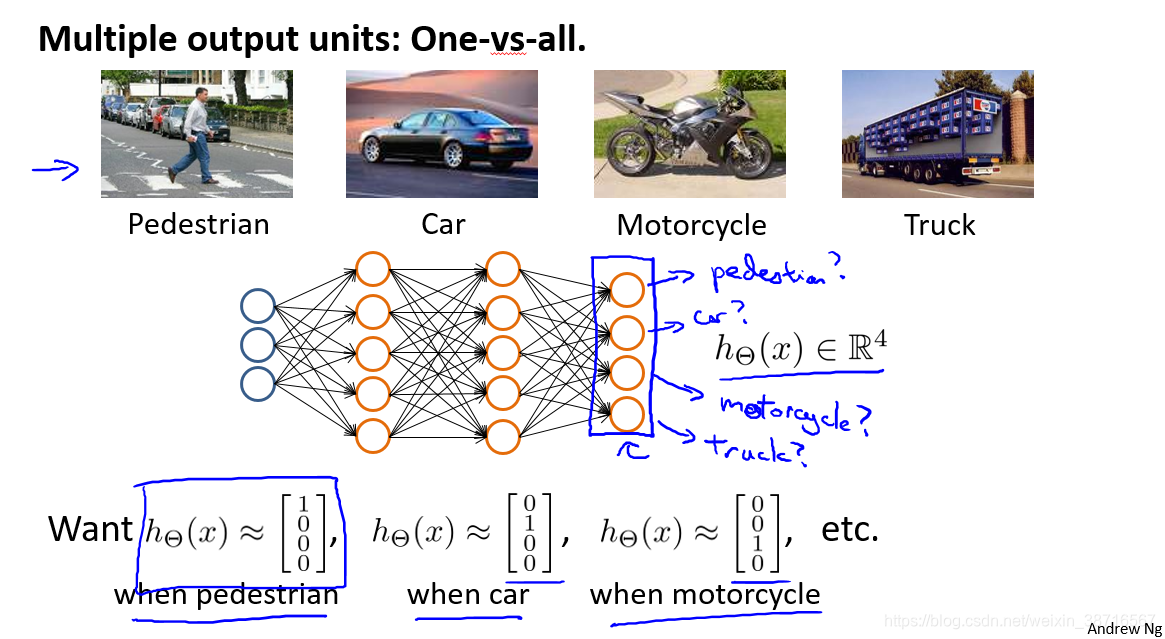
如何实现如同这里更复杂的神经网络呢？\downarrow

Graph Neural Networks: A Review of Methods and Applications（图神经网络：方法与应用综述）
weixin_41697507的博客
07-06 5761
Graph Neural Networks: A Review of Methods and Applications Jie Zhou , Ganqu Cui , Zhengyan Zhang , Cheng Yang, Zhiyuan Liu, Lifeng Wang, Changcheng Li, Maosong Sun Abstract—Lots of learning tasks req...
[论文解读]All in one：: Multi-Task Prompting for Graph Neural Networks图神经网络的多任务提示
强化学习曾小健
02-26 1941
这个函数可能是对提示图参数进行操作的某种计算，比如根据这些参数生成新的节点表示，或者更新模型的状态以适应新任务。在不同的上下文中，函数 f(θ) 可以有不同的具体含义，它通常会涉及到如何使用这些参数来影响模型的行为或其对数据的处理方式。不过，由于我无法直接查看PDF文件的内容，所以这里的解释是基于常见的机器学习和深度学习术语的一般性解释。提示图是一种用于调整预训练模型以适应特定任务的结构，这些参数可能包括用于构造提示的节点和边的权重，或者其他用于定义提示图结构的属性。与原始图 G 结合后的新表达式。
【matlab代码】单缝衍射（菲涅尔衍射 弗朗禾费衍射）
04-25
这是几个程序包，matlab代码，里面是单缝衍射，包括菲涅尔衍射和弗朗禾费衍射的光强分布图，希望对用到这一点的同学或者网友有所帮助，谢谢。
Machine Learning - Neural Networks Representation Part I
iracer的博客
03-12 1922
This article is about the model representation of Neuron Network. It contains the topics about nonlinear hypotheses, neurons and the brain, model representation.
coursera Machine Learning 第四周 测验quiz答案解析 Neural Networks: Representation
sinat_39805237的博客
12-04 6402
1.选择 解析：A.正确。因为是sigmoid函数，只能取0或者1。 B. C.两层解决不了XOR问题，至少三层，从课件就可看出。 D.
吴恩达《Machine Learning》-Neural Networks Representation神经网络介绍（八）
丰brother的博客
06-17 437
对于特征很多的情况，采用 polynomial regression 多项式回归会产生指数型的时间复杂度。O（n^3）(次方数=多项式多少阶) 图像特征处理： 按像素点处理 练习题： 选择（C）像素点共有100100=110^4 quadratic terms 平方项为n2/2时间复杂度为o(n2) 故 （104）2/2=5*10^7 神经网络原理： 将听觉的脑皮层，连接到视觉信号，听觉...
吴恩达学习笔记—— 第八、神经网络：表述
hfut天天的博客
02-16 270
吴恩达机器学习 学习记录
图（Graph）和 图神经网络（Graph Neural Networks, GNN）
最新发布
Rhett_Butler0922的博客
04-28 843
图（Graph）是一种表示实体及其关系的数据结构，数学上定义为 G=(V,E)G = (V, E)G=(V,E)，其中：图的类型包括：每个节点可以有特征向量 xv∈RFx_v \in \mathbb{R}^Fxv​∈RF，表示节点的属性；边也可以有特征 euve_{uv}euv​，表示关系的属性。图神经网络（Graph Neural Networks, GNN） 是一类专门设计用于处理图结构数据的神经网络。GNN通过利用图的拓扑结构（节点和边的连接关系），学习节点、边或整个图的表示（embedding），用
Machine Learning (4) Motivations & Neural Networks
Neil の Workshop
09-20 244
这一节将开始介绍关于神经网络的相关内容。 1. Motivations [动机]：（略）。 2. Neural Networks [神经网络]： 2.1 Model Representation (1) [ 模型表示法（1）]： 2.1.1 让我们从非常简单的神经元的机理来讨论这个问题，神经元可以看做是一个计算单元，其从树突（们）[Dendrites]接收输入，这些输入可以被当做带电输入（...
中英双语面试、笔试题 -- 计算机视觉(1) : 神经网络基础；Computer Vision Interview (1) :Fundamentals of Neural Networks
shiter编写程序的艺术
09-17 288
*随机梯度下降（Stochastic Gradient Descent, SGD）**是机器学习中常用的一种优化算法，其目的是最小化损失函数（或称为目标函数、成本函数）。与标准梯度下降方法不同，标准梯度下降计算整个训练数据集关于模型参数的梯度并据此更新参数，而随机梯度下降则在每次迭代时仅利用一个训练样本来估计梯度，并据此调整参数。
用多级衍射全息光栅实现神经网络的光学互连 (2000年)
06-12
用Mach Zehnder干涉仪分两步记录制作了具有多级衍射的全息光栅.再利用其多级衍射效应,实现了1 D神经网络的光学互连.结果表明,应用该方法不仅能得到满意的光学互连,且具有简单易行的优点.
wavefront-sensor-neural-network:经过训练的神经网络，通过测量物体的衍射图来检索物体的振幅和相位
04-13
波前传感器神经网络 经过训练的神经网络，通过测量物体的衍射图来检索物体的振幅和相位 出版物： 通过人工神经网络实现实时相位检索和波前感测乔纳森·怀特（Jonathon White），西西·王（Sici Wang），威廉·埃申（Wilhelm Eschen）和扬·罗斯哈特（Jan Rothhardt） 安装 pip install -r requirements.txt 概述/按重要性顺序说明的文件 run_tests.sh 要训​​练网络，请运行shellscript'run_tests.sh'。 这将调用多个.py文件来创建用于训练的新数据集，向数据集添加人为噪声，然后训练神经网络。 在该文件中指定了用于训练网络的参数，这些参数是训练样本的数量，训练数据的噪声级别的峰值计数以及波前传感器。 noise_test_compareCDI.sh 加载经过训练的网络，并在几个测试样本上进
Machine Learning - Neural Networks Learning: Backpropagation in Practice
iracer的博客
04-23 4291
This article is the notes of machine learning week 5, Neural Networks Learning. It contains topic about how to apply Backpropagation algorithm in practice.
什么是神经网络？用代码示例解析其工作原理
Gefangenes的博客
07-02 642
训练神经网络的过程通常包括使用大量输入数据和期望输出，计算损失函数（用于衡量网络输出与期望输出之间的差距），并使用优化算法（如梯度下降法）调整权重以最小化损失。梯度的方向是函数在该点处变化最快的方向，梯度的大小表示函数在该点处的变化速率。在上面的代码示例中，我们计算了输出层的误差（output_error），这个误差实际上就是损失函数的梯度。：利用若干个权重系数矩阵W,偏倚向量b来和输入值向量x进行一系列线性运算和激活运算，从输入层开始，一层层的向后计算，一直到运算到输出层，得到输出结果为值。
(2018)All-optical machine learning using diffractive deep neural networks
taochenning的博客
09-03 8817
这篇文章提出全光衍射深度神经网络（Diffractive Deep Neural Network, D2NN）。D2NN的训练由计算机实现，完成训练后的网络由3D打印的被动衍射层构成，可以光速完成各种复函数运算。目前D2NN已实现手写数字识别、简单物体分类、成像镜的功能，并且D2NN在全光图像分析、特征检测、目标分类及新型相机设计等领域都将具有很多的应用。
Diffractive-Deep-Neural-Networks 项目亮点解析
gitblog_00949的博客
04-23 467
Diffractive-Deep-Neural-Networks 项目亮点解析 1. 项目的基础介绍 Diffractive-Deep-Neural-Networks 是一个基于深度学习原理的开源项目，主要研究并实现了衍射深度神经网络（Diffractive Deep Neural Networks，简称DDNN）。该网络利用衍射原理来模拟神经网络的前向传播和反向传播过程，旨在探索新型计算架构以提...
【免费下载】 Diffractive-Deep-Neural-Networks 项目教程
gitblog_01150的博客
10-11 2272
Diffractive-Deep-Neural-Networks 项目教程 1. 项目介绍 Diffractive-Deep-Neural-Networks（D2NN）是一个开源项目，旨在通过衍射深度神经网络实现全光机器学习。该项目是基于论文 "All-optical machine learning using diffractive deep neural networks&quot...
光子神经网络的应用及发展概述
weixin_45890678的博客
08-25 9375
光子神经网络的应用及发展概述 最近研读光子神经网络论文，完成一个简单综述作为课程论文 参考https://blog.youkuaiyun.com/taochenning/article/details/106305319 1 引言 目前，人工智能作为当今计算机科学最为活跃的领域之一，在计算机视觉、自然语言处理、自动驾驶以及目标跟踪等领域有着广泛的应用。人工神经网络（Artificial Neural Network，ANN）成为20世纪80 年代以来人工智能领域兴起的研究热点，通过模仿神经系统结构，建立神经网.
Fashion-MNIST数据集发布一周年，论文引用量超250篇
Paper weekly
10-08 2079
作者简介：肖涵博士，Fashion-MNIST 数据集作者。现为腾讯 AI 部门高级科学家、德中人工智能协会主席。他曾于 2014-2018 年初就职于位于德国柏林的 Z...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值