unscented kalman filter

最新推荐文章于 2025-06-17 21:57:23 发布
原创 最新推荐文章于 2025-06-17 21:57:23 发布 · 1.4k 阅读 · 5 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#算法

本文深入探讨了UKF（无迹卡尔曼滤波）的工作原理及其在非线性系统中的优势与挑战。与EKF相比，UKF通过无迹变换避免了线性化误差，但在高维状态和强非线性情况下可能面临稳定性问题。文章详细解释了如何选择sigma点和设置权重，以及UKF算法的具体步骤。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

UKF 原理及仿真

UKF的优势

  • EKF是线性卡尔曼滤波，会引入线性化误差
  • EKF需要计算Jacobian矩阵，不易实现

UKF的问题

  • 低维状态仿真效果超好，实际生产过程中的高维状态使用ukf非常不稳定
  • 此方法在非线性程度小的时候，可以削弱非线性的影响。弱点是当非线性程度强的时候，协方差的更新容易出现负定矩阵的情况。

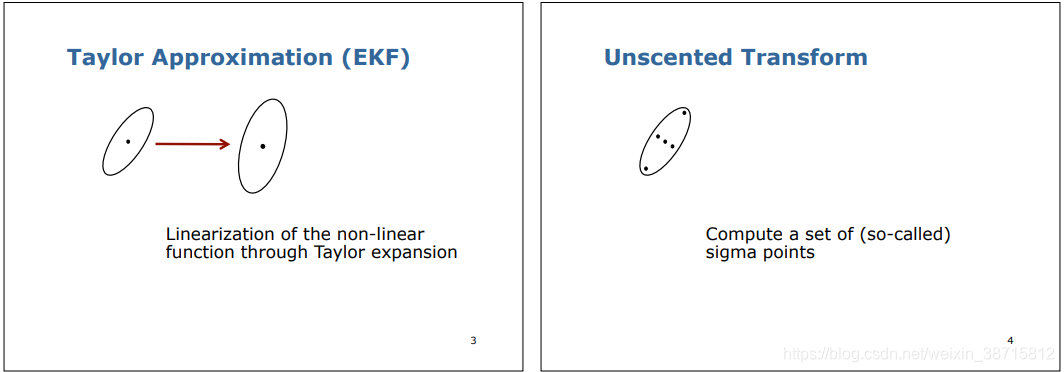
UKF原理

并不对非线性方程f和h在估计点处做线性化逼近，而是利用无迹变换在估计点附近确定采样点，用这些点的高斯密度来近似状态的概率密度函数
In general, n + 1 \bm{n+1} n+1 sigma points are necessary and sufficient to define a discrete distribution having a given mean and covariance in n \bm{n} n dimensions.
在这里插入图片描述

UKF 步骤

steps

  1. Compute a set of sigma points（这些点的均值和协方差等于原状态分布的均值和协方差）
  2. Each sigma points has a weight
  3. Transform the point through the nonlinear function（状态方程）
  4. Compute a Gaussian from weighted points
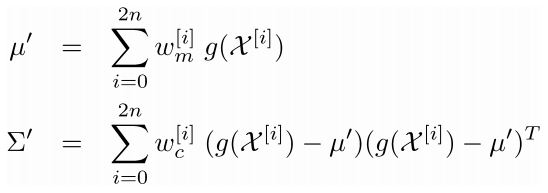
    计算高斯模型

two problems

How to choose the sigma points?

A canonical set of sigma points is the symmetric set originally proposed by Uhlmann.

  • 选择的sigma点满足以下式子：
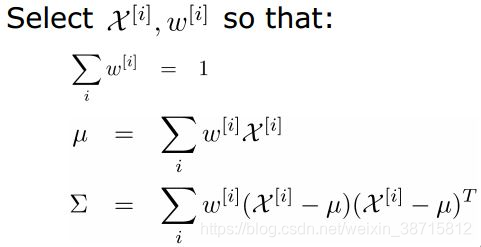
    在这里插入图片描述
  • 第一个点选择均值，其余点根据另外两个式子选择：
    在这里插入图片描述

How to set the weights?

在这里插入图片描述

其他参数的选择

在这里插入图片描述

UKF 算法

在这里插入图片描述

无迹卡尔曼滤波 (UKF, Unscented Kalman Filter) 算法详解及案例分析
qq_42568323的博客
01-15 1797
无迹卡尔曼滤波是一种用于估计非线性系统状态的递归算法。其目标是通过结合系统模型和观测数据，估计系统的最优状态。
无迹卡尔曼滤波 (Unscented Kalman Filter)
Frankgoogle的博客
04-15 1万+
最近读了一篇文献，里面用到了无迹卡尔曼滤波(Unscented Kalman Filter)。这里写一下我对这种方法的理解。卡尔曼滤波的理解部分可以参考我之前的文章。 我的一点点理解 无迹卡尔曼滤波是对卡尔曼滤波的一种改进。这种改进主要是针对非线性的信号。因为在卡尔曼滤波中，预测模型以及测量空间对应的转换矩阵都是都是线性转换。但是在面对非线性信号时，会出现无法拟合的情况。所以就有了无迹卡尔曼滤波。...
Unscented Kalman filter无迹卡尔曼滤波
热门推荐
hanmoge的博客
02-10 1万+
扩展卡尔曼滤波（EKF）用一阶导数来对非线性模型做局部线性化，而无迹卡尔曼滤波UKF使用所谓“统计线性化”方法，从一个已知的分布中做采样，也就是“生成sigma points”，来“模拟”非线性模型的随机分布。UKF也包含经典的“预测”和“更新”过程，只不过多了一步sigma points的采样。
【EKF、UKF、PF、EPF、UPF】改进的粒子滤波算法及其应用研究附Matlab代码
最新发布
Matlab_jiqi的博客
06-17 736
在现代信号处理与状态估计领域，滤波算法扮演着至关重要的角色，它们能够从含有噪声的观测数据中提取出准确的目标状态信息。粒子滤波（PF）算法作为一种基于蒙特卡洛模拟的非线性滤波方法，在处理复杂非线性、非高斯系统时展现出独特优势，但也存在粒子退化、计算量大等问题。而扩展卡尔曼滤波（EKF）、无迹卡尔曼滤波（UKF）以及基于粒子滤波衍生出的期望传播粒子滤波（EPF）、无迹粒子滤波（UPF）等算法，从不同角度对传统滤波算法进行改进和优化。本文将深入研究这些算法的原理、改进思路及其在实际场景中的应用。
Basics Algorithms|无迹卡尔曼滤波器(Unscented Kalman Filter, UKF)
TURBOTX的博客
05-29 984
Unscented Kalman Filter is an improved version of the Kalman Filter. It utilized an unscented transform to incorporate non-linearity within the model.The parameters optimized here are , and . 1.贝叶斯估计(Bayes Estimation) 许多系统需要由带噪声的传感器度量来估计系统状态，如机器人控制、股票..
滤波估计理论（四）——无迹卡尔曼滤波（Unscented Kalman Filter）
weixin_43991178的博客
08-01 4085
滤波估计理论（四）——无迹卡尔曼滤波（Unscented Kalman Filter）无迹变换（Unscented Transform） 在EKF中我们使用泰勒级数近似非线性函数是为了利用Gaussian的线性性质进行期望（均值）和方差的传递，但在线性化过程中，由于线性化点的选择和高阶项的舍弃，将不可避免的存在线性化误差。如果我们能找到一种方法直接获得非线性变换之后的期望和方差，就可以避免由线性化...
Unscented-Kalman过滤器车辆跟踪：通过使用Unscented卡尔曼过滤器融合嘈杂的激光雷达和雷达测量，在模拟的高速公路交通上对多辆汽车进行状态估计和跟踪
02-15
无味卡尔曼滤波器车辆跟踪 在该项目中，实现了无味卡尔曼滤波器，以使用嘈杂的激光雷达和雷达测量来跟踪和估算高速公路上多辆汽车的状态，如图所示。 main.cpp正在使用highway.h来创建一个直行的3车道高速公路环境，其中有3辆交通汽车和主要的自我汽车在中心。 观看者场景以自我汽车为中心，坐标系也相对于自我汽车。 自我汽车为绿色，而其他交通汽车为蓝色。 交通车辆将加速并改变其转向以改变车道。 每辆运输车都有自己的UKF对象生成，并将在每个时间步更新每个独立的对象。 汽车上方的红色球体表示（x，y）激光雷达检测，紫色线显示雷达测量值以及沿检测角度的速度大小。 跟踪仅沿X / Z轴进行。 跟踪不考虑Z轴。 其他重要依赖 cmake> = 3.5 所有操作系统： make> = 4.1（Linux，Mac），3.81（Windows） Linux：大多数Linux发行版默认都安装
An adaptive unscented Kalman filter-based adaptive tracking control for wheeled mobile robots with control constrains in the presence of wheel slipping
02-11
本文提出了一种基于适应性无迹卡尔曼滤波器（Adaptive Unscented Kalman Filter, AUKF）的自适应跟踪控制方法，用于解决轮式移动机器人在未知车轮滑动情况下的轨迹跟踪问题。该方法主要由以下几个关键步骤构成： 1....
Unscented Kalman Filter Tutorial
02-09
Unscented Kalman Filter Tutorial无迹卡尔曼滤波简介：Gabriel A. Terejanu Department of Computer Science and Engineering, University at Buffalo
042_Unscented Kalman Filter in Matlab无迹卡尔曼滤波
withstand的博客
12-15 995
无迹卡尔曼滤波(Unscented Kalman Filter, UKF)是一种基于卡尔曼滤波的非线性状态估计方法，它通过一种称为无迹变换(Unscented Transformation)的方法，将非线性系统的状态估计问题转化为线性系统的状态估计问题，然后使用卡尔曼滤波器进行状态估计。这是一种在线方法，也就是说，它会连续地对系统状态进行估计，而不是像批处理方法那样，一次性处理所有的数据。假设我们对 van der Pol Oscillator 的状态进行观测，但是观测值是带有噪声的。系统的框图如上所示。
无损卡尔曼滤波器（Unscented Kalman Filter, UKF)#附MATLAB代码
weixin_44060636的博客
08-22 3963
无损卡尔曼滤波 概念 无损卡尔曼滤波又称无迹卡尔曼滤波（Unscented Kalman Filter，UKF），是无损变换（Unscented Transform，UT）与标准卡尔曼滤波体系的结合，通过UT变换使非线性系统方程适用于线性假设下的标准卡尔曼体系。 而扩展卡尔曼滤波（Extended Kalman Filter，EKF）通过线性化非线性函数实现递推滤波，通常采用泰勒级数展开，然后求取雅克比矩阵，其精度低，计算复杂。 无损变换（Unscented Transform，UT） UT变换是用固定数量
UKF（Unscented Kalman Filter) 无迹卡尔曼滤波程序代码
06-05
本代码实现是对UKF（无迹卡尔曼滤波）的MATLAB实现
无迹卡尔曼滤波_自动驾驶基础技术(七)-无迹卡尔曼滤波Unscented Kalman Filter
weixin_39787057的博客
12-18 497
Unscented Kalman Filter是解决非线性卡尔曼滤波的另一种思路，它利用Unscented Transform来解决概率分布非线性变换的问题。UnScented Kalman Filter不需要像Extended Kalman Filter一样计算Jacobin矩阵，在计算量大致相当的情况下，能够获得更加精确非线性处理效果。1.Unscented Kalman Filter的思想i...
无迹卡尔曼滤波
wxj1yx的博客
10-07 413
一文理解无迹卡尔曼滤波器
无迹卡尔曼滤波（Unscented Kalman Filter, UKF）：理论和应用
weixin_39753819的博客
01-15 3545
卡尔曼滤波是一种强大的状态估计方法，广泛应用于控制系统、导航、机器人等领域。然而，传统的卡尔曼滤波假设系统是线性的，而在实际应用中，许多系统具有非线性特性。为了解决这一问题，无迹卡尔曼滤波（Unscented Kalman Filter, UKF）应运而生，它通过采用无迹变换来处理非线性系统。
利用Unscented Kalman滤波器实现目标跟踪
gitblog_00050的博客
06-10 330
利用Unscented Kalman滤波器实现目标跟踪 在这个开源项目中，我们探索了一个独特且高效的方法来跟踪移动对象，如行人或车辆，通过结合LIDAR和RADAR传感器数据，利用了非线性估计领域的利器——Unscented Kalman滤波器（UKF）。 项目简介 这个项目的目标是超越传统的基于线性方程的Kalman滤波器，特别是在处理复杂的非线性问题时。UKF不依赖于线性化，而是采用一种更为智...
Unscented kalman Filtering 无损卡尔曼滤波的matlab程序
张文宇的博客
02-07 7638
本来想写下原理的，优快云的博客貌似不可以编辑公式，那就算了，直接放程序好了。 这个程序大部分是从前人那里看来的，向他们表示感谢，它帮助我完成了一个课程论文的仿真。我很喜欢原作者简洁有效的编程风格。这几个程序对于学习最优估计课程的人来说是很需要的。 构建Sigma点的函数 function X = sigmas(x,P,c) %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
python 无迹卡尔曼（filterpy.kalman.UnscentedKalmanFilter）调参
weixin_46180132的博客
05-20 5130
python 无迹卡尔曼（filterpy.kalman）调参 1. filter.kalman.MerweScaledSigmaPoints，Van der Merwe式sigma点选择，UT变换最好用的sigma点选择算法 input： n ：状态维度 alpha ：均值附近sigma点的分布，通常选0.1~1之间。调节中心点与周围点的权重。 beta ：由先验知识，高斯分布选2。 kappa ：k = 3-n output: Wm ：sigma点均值的权重 Wc ：sigma点协方差的权重 可以看到，
解析MATLAB中的unscentedKalmanFilter函数
qq_43131852的博客
05-31 1604
unscentedKalmanFilter函数 obj = unscentedKalmanFilter(StateTransitionFcn,MeasurementFcn,InitialState,Name,Value) 1.输入参数 StateTransitionFcn：状态方程。形式取决于您在对象中设置的HasAdditiveProcessNoise属性指定噪声为加性还是非加性： HasAdditiveProcessNoise为true ——过程噪声w是累加的，并且状态转换函数指定状态如何在上一个时
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值