| 时间avg | 时间min | 时间max | 空间avg | 稳定性 |
| O(nlog(n))
| O(nlog(n)) (此处可优化最小时间复杂度至o(n)见代码注释及下图)
| O(nlog(n))
| o(n)(Divide-and-Conqure) 临时数组在合并后空间会释放 o(1)(In-place Algorithm原地归并排序 | 稳定性:取决于合并函数的写法 (若以[start:middle]<=[middle:terminal]做判断则稳定,反之不稳定) |
优:稳定
缺:空间复杂度为o(n),以空间换时间。算法中需要来回复制结果数组和原序列,很耗时,所以归并排序一般用于外排序
适用:数列较大且要求稳定
归并排序改进措施
- 直接将辅助数组作为参数传入,而不直接使用静态数组
- 小排序问题:划分为小序列,做直接插入排序,再采用归并排序。一般可以将归并排序的时间缩短 10% ~ 15%;
- 判断测试数组是否已经有序:如果 arr[mid] <= arr[mid+1],我们就认为数组已经是有序的并跳过merge() 方法,可以是任意有序的子数组算法的运行时间变为线性的。
- 不回写:这个策略是最重点要讲述的策略。写回操作在大排序问题时非常浪费时间,我们就思考一种不回写策略来解决这个问题。merge() 方法中不将元素复制到辅助数组,节省数组复制的时间。调用两种排序方法,一种:将数据从输入数组排序到辅助数组;另一种:将数据从辅助数组排序到输入数组。
重点:在每个层次交换输入数组和辅助数组的角色。 - 最长无逆序子序列:我们经过分析知道,归并排序的基础是两个有序子序列的合并,那么我们可以通过寻找最长无逆序子序列来优化归并排序的比较次数。例如,(4,5,6,3,7,1)这个序列,我们找到三个无逆序子序列,直接对这三个子序列进行合并即可,减少比较次数。
- 递归:消除递归,避免递归过程的时间消耗。
package main.Test;
/**
* 归并排序优化方案
*/
public class GuiBingSort {
// 数组的长度为 7 时,切换
private static final int CUTOFF = 7;
private static void merge(Comparable[] src, Comparable[] dst, int lo, int mid, int hi) {
int indexI = lo;
int indexJ = mid + 1;
for (int indexK = lo; indexK <= hi; indexK++) {
if (indexI > mid) {
dst[indexK] = src[indexJ++];
} else if (indexJ > hi) {
dst[indexK] = src[indexI++];
} else if (less(src[indexJ], src[indexI])) {
dst[indexK] = src[indexJ++];
} else {
dst[indexK] = src[indexI++];
}
}
}
// 递归方式
private static void sort(Comparable[] src, Comparable[] dst, int lo, int hi) {
// 优化方案②:应该在子数组长度为 7 的时候切换到插入排序
if (hi <= lo + CUTOFF) {
insertionSort(dst, lo, hi);
System.arraycopy(dst, lo, src, lo, hi - lo + 1);
return;
}
int mid = lo + ((hi - lo) >> 1);
// 优化方案④:在每个层次交换输入数组和辅助数组的角色
sort(dst, src, lo, mid);
sort(dst, src, mid + 1, hi);
//优化方案③:判断测试数组是否已经有序
if (!less(src[mid + 1], src[mid])) {
System.arraycopy(src, lo, dst, lo, hi - lo + 1);
return;
}
// 优化方案④:merge() 方法中不将元素复制到辅助数组
merge(src, dst, lo, mid, hi);
}
// 非递归
private static void sort(Comparable[] src, Comparable[] dst) {
int n = src.length;
int len = 1;
int flag = 1;
while (len < n) {
if (flag == 1) {//通过flag来判定当前是奇数回合还是偶数回合
flag = 0;
int i;
if (len <= CUTOFF) {
for (i = 0; i < n + 1 - 2 * len; i = i + 2 * len) {
insertionSort(dst, i, i + 2 * len - 1);
System.arraycopy(dst, i, src, i, 2 * len);
}
if (i + len - 1 < n) {
insertionSort(dst, i, n - 1);
System.arraycopy(dst, i, src, i, n - i);
} else {
for (; i < n; i++) dst[i] = src[i];
}
} else {
for (i = 0; i < n + 1 - 2 * len; i = i + 2 * len) {
merge(src, dst, i, i + len - 1, n - 1);
}
if (i + len - 1 < n) {
merge(src, dst, i, i + len - 1, n - 1);
} else {
for (; i < n; i++) dst[i] = src[i];
}
}
len *= 2;
} else {
flag = 1;
int i;
if (len <= CUTOFF) {
for (i = 0; i < n + 1 - 2 * len; i = i + 2 * len) {
insertionSort(src, i, i + 2 * len - 1);
System.arraycopy(src, i, dst, i, 2 * len);
}
if (i + len - 1 < n) {
insertionSort(src, i, n - 1);
System.arraycopy(src, i, dst, i, n - i);
} else {
for (; i < n; i++) src[i] = dst[i];
}
} else {
for (i = 0; i < n + 1 - 2 * len; i = i + 2 * len) {
merge(dst, src, i, i + len - 1, n - 1);
}
if (i + len - 1 < n) {
merge(dst, src, i, i + len - 1, n - 1);
} else {
for (; i < n; i++) src[i] = dst[i];
}
}
len *= 2;
}
}
if (flag == 1) {
for (int p = 0; p < n; p++) {
dst[p] = src[p];
}
}
}
// 入口
public static void sort(Comparable[] dst, int type) {
// 优化方案①:直接将辅助数组作为参数传入
Comparable[] src = dst.clone();
if (type == 0) {
sort(src, dst, 0, dst.length - 1);
} else if (type == 1) {
sort(src, dst);
}
}
private static void insertionSort(Comparable[] arr, int lo, int hi) {
for (int indexI = lo; indexI <= hi; indexI++) {
for (int indexJ = indexI; indexJ > lo && less(arr[indexJ], arr[indexJ - 1]); indexJ--) {
exchange(arr, indexJ, indexJ - 1);
}
}
}
/**
* 比较两个元素的大小
*
* @param comparableA 待比较元素A
* @param comparableB 待比较元素B
* @return 若 A < B,返回 true,否则返回 false
*/
private static boolean less(Comparable comparableA, Comparable comparableB) {
return comparableA.compareTo(comparableB) < 0;
}
/**
* 将两个元素交换位置
*
* @param arr 待交换元素所在的数组
* @param indexI 第一个元素索引
* @param indexJ 第二个元素索引
*/
private static void exchange(Comparable[] arr, int indexI, int indexJ) {
Comparable temp = arr[indexI];
arr[indexI] = arr[indexJ];
arr[indexJ] = temp;
}
/**
* 打印数组的内容
*
* @param arr 待打印的数组
*/
private static void show(Comparable[] arr) {
for (int index = 0; index < arr.length; index++) {
System.out.print(arr[index] + " ");
}
System.out.println();
}
/**
* 判断数组是否有序
*
* @param arr 待判断数组
* @return 若数组有序,返回 true,否则返回 false
*/
public static boolean isSort(Comparable[] arr) {
for (int index = 1; index < arr.length; index++) {
if (less(arr[index], arr[index - 1])) {
return false;
}
}
return true;
}
public static void main(String[] args) {
Comparable[] a = {102,1,2,4,3,6,3,5,2,1002,1223,1212};
sort(a, 1);
System.out.println(isSort(a));
show(a);
}
}








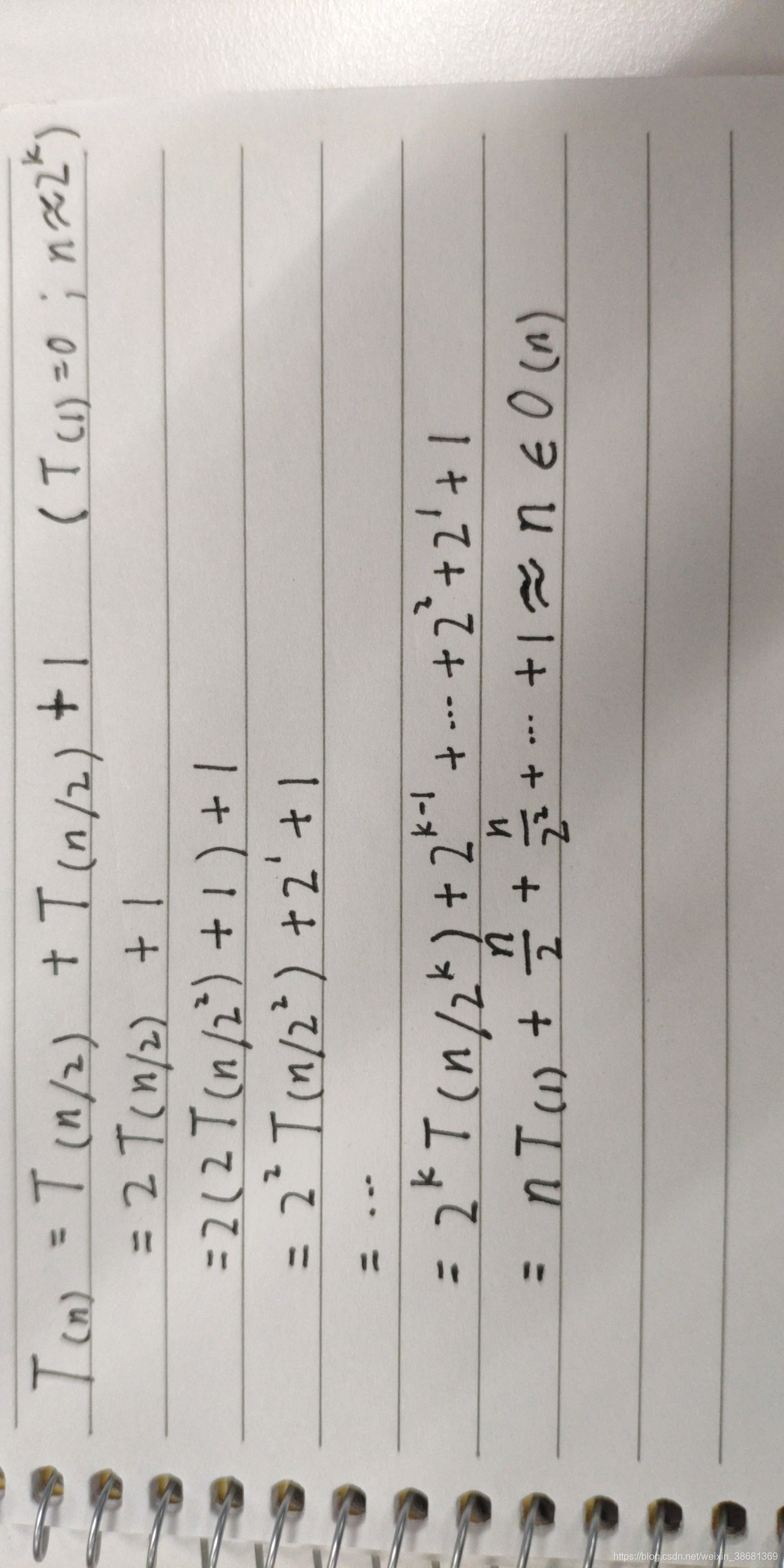

















 630
630

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








