手把手拆解三大复杂算法（归并排序）

嗨，大家好，这是排序算法篇第6篇文章

其它算法可在我的合集查看

后续会继续更新其它算法相关内容！

目录

一、算法介绍

 二、算法原理与实现

三、时空复杂度分析

四、总结

---

一、算法介绍

归并排序（Merge Sort）是一种基于分治法​（Divide and Conquer）的排序算法，核心思想是将一个无序数组递归拆分成最小单元，再逐步合并成有序序列

。整个过程可以抽象为以下两步：

1. ​分割：将数组不断二分，直到每个子数组只剩一个元素（此时天然有序）。
2. ​合并：将两个有序子数组合并为一个更大的有序数组，直至所有元素合并完毕

 二、算法原理与实现

其实归并排序原理很简单，就是先拆开，再合并

假设有两个有序数组，我们只需要比较他们最靠前的元素谁小，就先拿下来

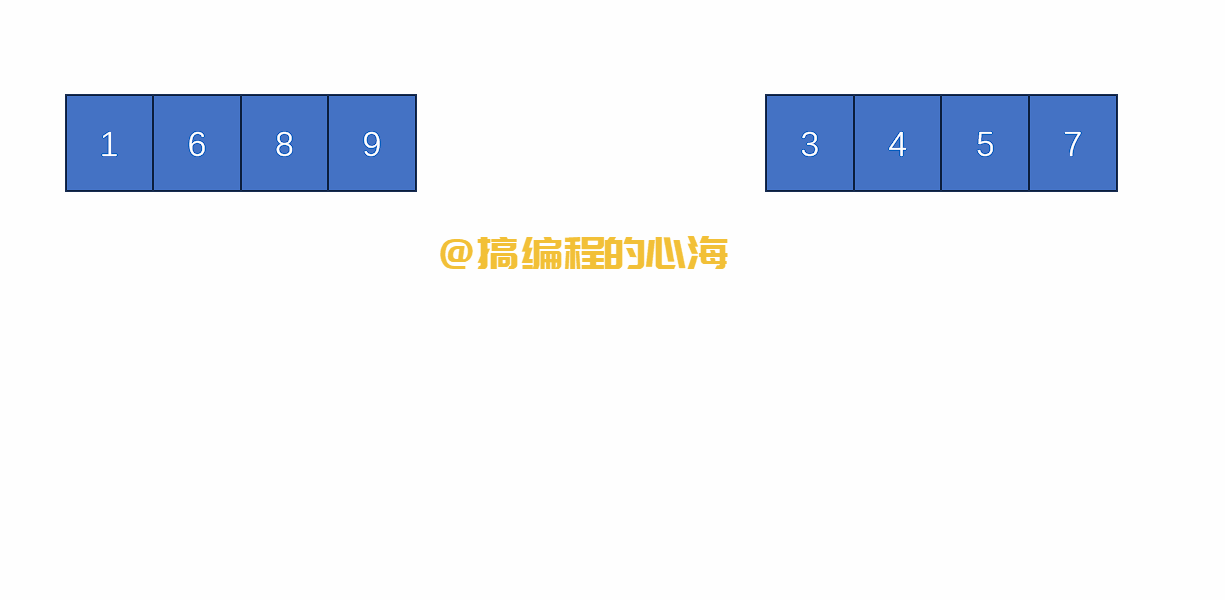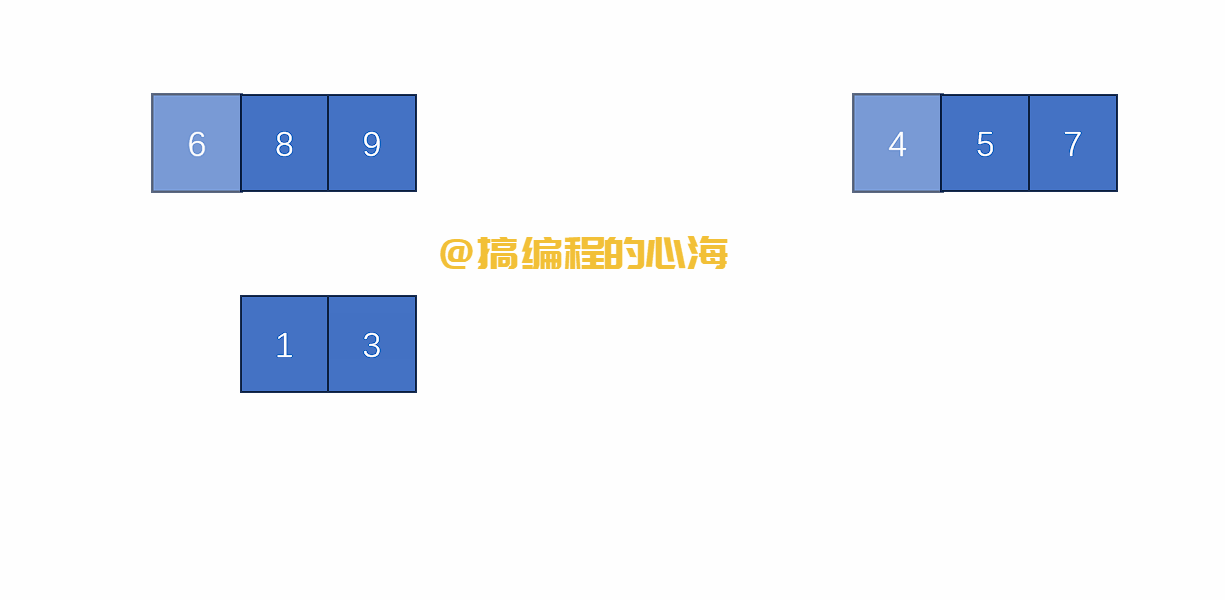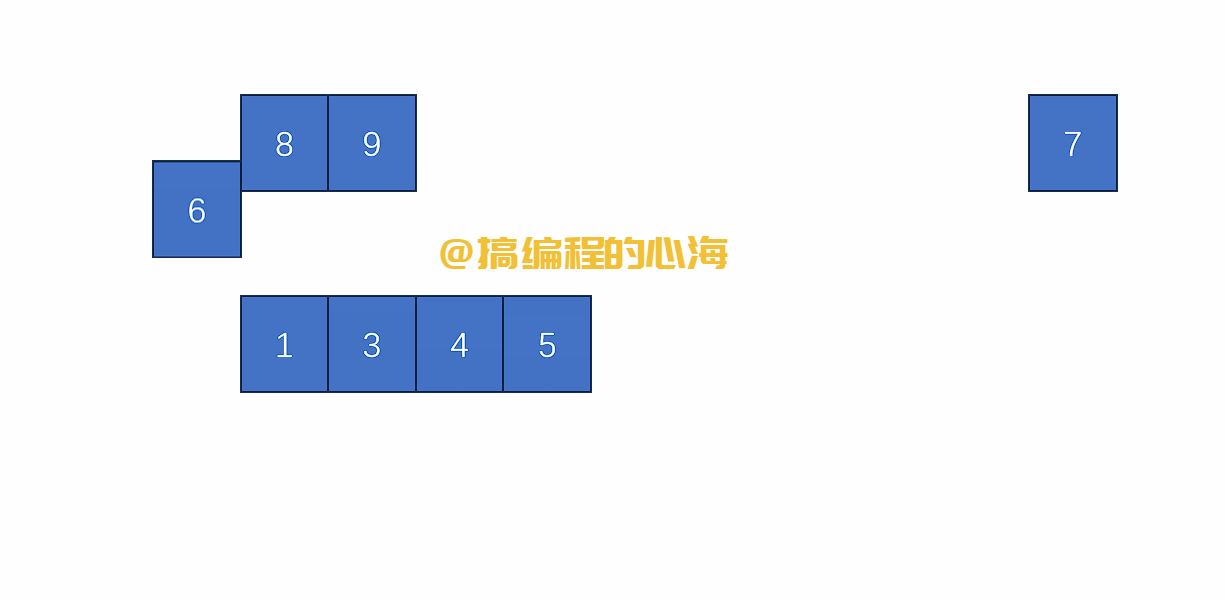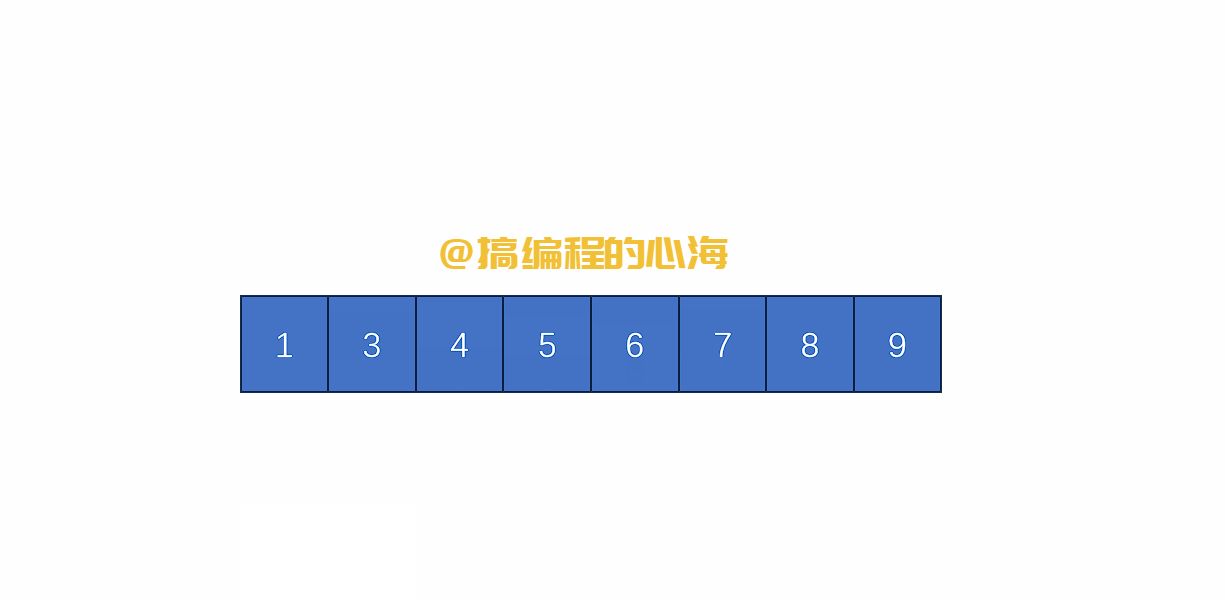
 那么，这两个有序的数组是哪来的？

就是通过对原数组不断拆分，直到最后只有一个元素时，一个元素就是最小有序数组

那么，据此我们就可以先编写一个合并函数，然后重复递归调用这个合并函数，即可实现归并排序

def merge(li, low, mid, high):
    # 初始化双指针：i指向左子数组起始位置，j指向右子数组起始位置
    i = low           # 左子数组起始下标（范围：low到mid）
    j = mid + 1       # 右子数组起始下标（范围：mid+1到high）
    tmp = []          # 临时数组，用于存储合并后的有序序列
    
    # 合并两个有序子数组（左：low~mid，右：mid+1~high）
    while i <= mid and j <= high:
        if li[i] < li[j]:
            tmp.append(li[i])  # 左子数组当前元素较小，加入临时数组
            i += 1
        else:
            tmp.append(li[j])  # 右子数组当前元素较小，加入临时数组
            j += 1
    
    # 处理左子数组剩余元素（若存在）
    while i <= mid:
        tmp.append(li[i])
        i += 1
    
    # 处理右子数组剩余元素（若存在）
    while j <= high:
        tmp.append(li[j])
        j += 1
    
    # 将合并后的有序序列覆盖回原数组的对应区间[low, high]
    li[low:high+1] = tmp

这里传入了几个参数，其中 li 是待排序数组，low ，high 是待排序区间的边界下标，mid 由 low 与 high 的和整除 2 得到，示意图如下

在 merge 函数中，关键点如下：

1. 双指针遍历：通过i和j分别遍历左右子数组，比较当前元素大小，将较小者加入临时数组
2. ​处理剩余元素：当一个子数组遍历完成后，另一个子数组的剩余元素直接追加到临时数组末尾
3. ​覆盖原数组：合并后的结果通过切片操作写回原数组的[low, high]区间

 有了这个函数，我们就只需要递归调用即可

def merge_sort(li, low, high):
    if low < high:   # 递归终止条件：当区间只有一个元素时停止分割
        mid = (low + high) // 2   # 计算中间分割点
        
        # 递归分割左子数组（low到mid）
        merge_sort(li, low, mid)
        
        # 递归分割右子数组（mid+1到high）
        merge_sort(li, mid+1, high)
        
        # 合并左右两个已排序的子数组
        merge(li, low, mid, high)

三、时空复杂度分析

时间复杂度：最优/最坏/平均均为 ​O(n log n)。如下图，总共 logn 层递归，每层数据为 n ，故时间复杂度O(nlogn)

​空间复杂度：​O(n)，主要来自合并时的临时数组

稳定性：稳定算法。合并时若元素相等，优先保留左侧元素顺序

四、总结

归并排序时间复杂度稳定为 O(n log n)，适合大规模数据。且是稳定排序，适用于需要保留元素原始顺序的场景（如多关键字排序）。

不足点在于，它需要额外 O(n) 空间，内存占用较高。

总的来说，数据量较大且对稳定性有要求（如数据库排序、外部排序）

后面会再整理一期内容，对比这六种常用算法（冒泡、选择、插入、快速、堆排、归并）

如果这篇文章对您有所启发，期待您的点赞关注！