UCB公式的理解

在解决探索与利用平衡问题时，UCB1 策略是一个很有效的方法，而探索与利用平衡问题中最经典的一个问题就是多臂赌博机问题（Multi-Armed Bandit）

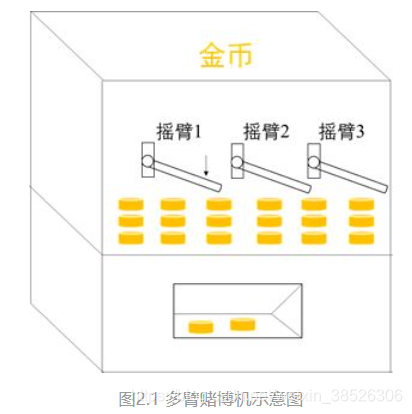
问题假设：按下摇臂后的回报取值为 1 或 0，每个摇臂获得回报的概率服从不同的分布，但事先并不知道
问题目标：按照某种策略来按压摇臂以获得最大的累计回报（咦，这不就是强化学习的目标嘛）
在这个问题中，探索与利用就是：
利用（exploitation）：按压之前获得回报概率最高的那个臂，以获得更高的累计回报。但是因为回报是随机的，对每个臂的回报概率的估计并不准确，或许真实回报概率最高的那个臂并非当前估计的那个臂。
探索（exploration）：随机地去按压不同的臂，得到每个臂更精确的回报概率估计，从而找到真实的那个最优的臂。但是要探索，就要去按压目前回报概率估计并不高的臂，意味着会损失一些按压高回报摇臂的机会。
窘境：因为尝试次数有限，所以探索和利用是矛盾的，加强一方必然削弱另一方。要想回报最大，则必须在探索和利用之中达成较好的平衡。
那如何来平衡探索和利用呢？

已有的方法包括 ϵϵ \epsilonϵ - greedy 策略和 softmax 策略，可以参考[2]进行了解，这里重点讲解对UCB1策略和公式的理解，见下图：

公式中如果只有第一项，那就是一个纯利用，也就是贪婪策略，它很容易陷入局部极值，而第二项的意义在于，如果我们对一个臂的了解过于少，那它的平均回报在此时的置信度是很低的，不确定度就很高，置信区间就很大（我想也可以理解为方差很大），我们就非常不相