java实现十大经典排序算法【GIF动画+完整代码+详细注释】

程序员三毛

已于 2023-12-26 22:10:27 修改

阅读量1.3k

点赞数 17

分类专栏：数据结构算法文章标签：排序算法 java 算法数据结构

于 2023-12-26 21:19:35 首次发布

本文链接：https://blog.youkuaiyun.com/weixin_38522648/article/details/135229621

版权

数据结构算法专栏收录该内容

2 篇文章

订阅专栏

引言

俗话说“千里之行，始于足下”。排序算法不仅是学习数据结构和算法的基础，而且是提高编程能力和解决实际问题的关键工具，无论是为了面试准备，还是为了提升编程技能，了解和掌握这些经典排序算法都是至关重要的。在本文中，我们将深入探讨十大经典排序算法的Java实现，配以动图示例和详细代码注释，助你一臂之力

目录结构

冒泡排序
选择排序
插入排序
希尔排序
快速排序
归并排序
堆排序
基数排序
计数排序
桶排序

冒泡排序

算法核心思想

比较相邻的元素。如果第一个比第二个大，就交换它们两个
对每一对相邻元素做同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数
针对所有的元素重复以上的步骤，除了最后一个
重复步骤1~3，直到排序完成

看下面这个动图示例：
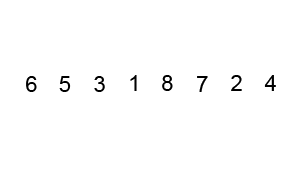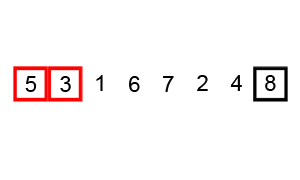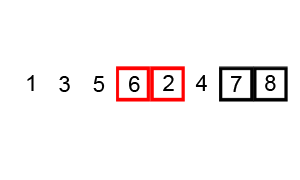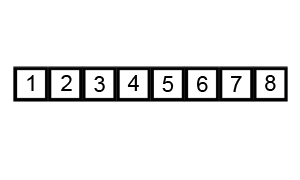
冒泡算法gif

代码实现

public void bubbleSort(int[] arr) {
    int n = arr.length;
    boolean swapped;
    for (int i = 0; i < n-1; i++) {
        swapped = false;
        for (int j = 0; j < n-i-1; j++) {
            if (arr[j] > arr[j+1]) {
                swapWithBitOperation(arr, j, j+1);
                swapped = true;
            }
        }
        // 如果在这一趟遍历中没有发生交换，说明数组已经排序完成
        if (!swapped)
            break;
    }
}

private void swapWithBitOperation(int[] arr, int i, int j) {
    if (arr[i] != arr[j]) {
        arr[i] = arr[i] ^ arr[j];
        arr[j] = arr[i] ^ arr[j];
        arr[i] = arr[i] ^ arr[j];
    }
}

用swapped这个标志位来标记在某一趟是否有发生过交换，如果在某一趟遍历中没有发生任何交换，这意味着数组已经排序完成，就可以提前结束排序过程
使用位运算交换两个元素，可以进一步提升代码运行效率，不需要临时变量，且操作速度更快

时间复杂度等分析

复杂度/稳定性	大O
最坏情况时间复杂度	O(n²)（数组完全逆序）
最好情况时间复杂度	O(n)（数组已经排序）
平均时间复杂度	O(n²)
空间复杂度	O(1)
是否稳定	稳定

选择排序

算法核心思想

每次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完

看下面这个动图示例：
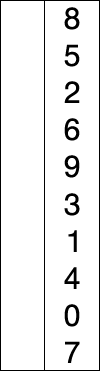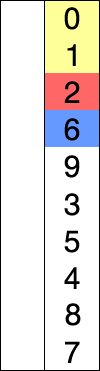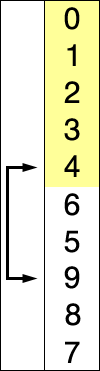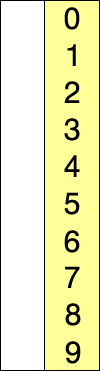
选择排序gif动图

代码实现

public void selectionSort(int[] arr) {
    int n = arr.length;

    for (int i = 0; i < n-1; i++) {
        int minIndex = i;
        for (int j = i+1; j < n; j++)
            if (arr[j] < arr[minIndex])
                minIndex = j;

        // 如果找到的最小元素不是当前位置的元素，则进行交换
        if(minIndex != i) {	
			// 位运算交换（参见冒泡排序）
            swapWithBitOperation(arr, i, minIndex);
        }
    }
}

时间复杂度等分析

复杂度/稳定性	大O
最坏情况时间复杂度	O(n²)
最好情况时间复杂度	O(n²)
平均时间复杂度	O(n²)
空间复杂度	O(1)
是否稳定	不稳定

插入排序

算法核心思想

初始排序：从第一个元素开始，该元素可以认为已经被排序
取出元素：取出下一个元素，在已经排序的元素序列中从后向前扫描
比较和移动：如果该元素（已排序）大于新元素，将该元素移到下一位置
重复步骤3：重复步骤3，直到找到已排序的元素小于或等于新元素的位置
插入元素：将新元素插入到该位置后
重复整个过程：重复步骤2~5

看下面这个动图示例：
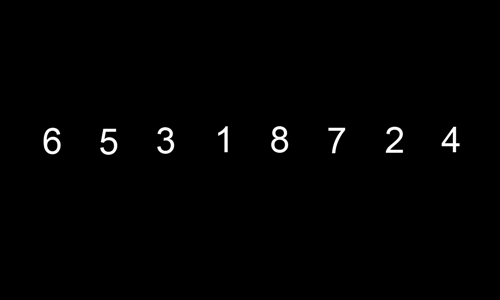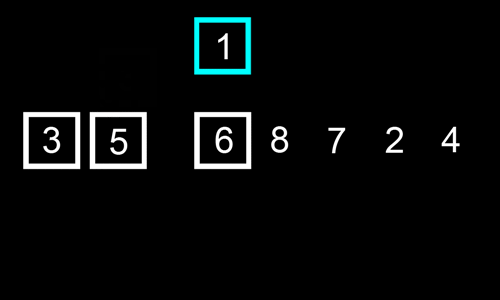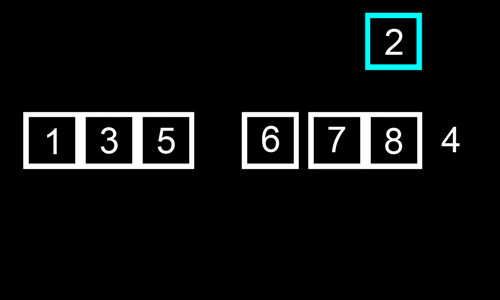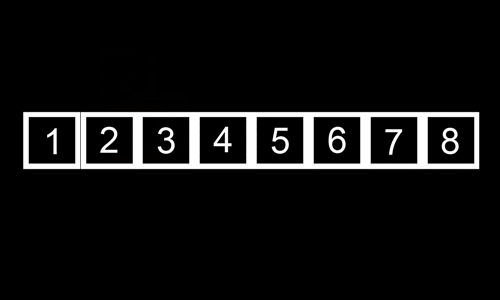
插入排序gf动图

代码实现

public void insertionSort(int[] arr) {
    int n = arr.length;
    for (int i = 1; i < n; ++i) {
        int key = arr[i];
        int j = i - 1;

        // 将大于 key 的元素向后移动
        while (j >= 0 && arr[j] > key) {
            arr[j + 1] = arr[j];
            j = j - 1;
        }
        arr[j + 1] = key;
    }
}

时间复杂度等分析

复杂度/稳定性	大O
最坏情况时间复杂度	O(n²)
最好情况时间复杂度	O(n²)
平均时间复杂度	O(n²)
空间复杂度	O(1)
是否稳定	不稳定

希尔排序

算法核心思想

希尔排序是一种基于插入排序的高效算法，其核心在于先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序，步骤如下：

选择间隔序列：根据序列长度选择一个间隔序列
分组插入排序：按照间隔序列分组，对每个组进行插入排序
减少间隔再排序：减少间隔序列的值，重复第2步，直到间隔为1
最终插入排序：执行一次标准的插入排序。

看下面这个动图示例：
希尔排序gif

代码实现

public class ShellSort {
    public static void sort(int[] array) {
        int n = array.length;

        // 从较大的间隔开始，逐步减小间隔
        for (int gap = n / 2; gap > 0; gap /= 2) {
            // 对每个间隔进行插入排序
            for (int i = gap; i < n; i += 1) {
                // 将array[i]插入到已经排序的序列中
                int temp = array[i];
                int j;
                for (j = i; j >= gap && array[j - gap] > temp; j -= gap)
                    array[j] = array[j - gap];

                // 将temp放到它应该在的位置
                array[j] = temp;
            }
        }
    }
}

时间复杂度等分析

复杂度/稳定性	大O
最坏情况时间复杂度	O(n²)
最好情况时间复杂度	O(n log n)
平均时间复杂度	取决于间隔序列
空间复杂度	O(1)
是否稳定	不稳定

快速排序

算法核心思想

快速排序是一种高效的排序算法，使用分而治之的策略来把一个序列分为两个子序列

选择基准：从数列中挑出一个元素，称为“基准”（pivot）
分区操作：重新排序数列，所有比基准值小的元素摆放在基准前面，所有比基准值大的元素摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作
递归排序：递归地将小于基准值元素的子数列和大于基准值元素的子数列排序

看下面这个动图示例：
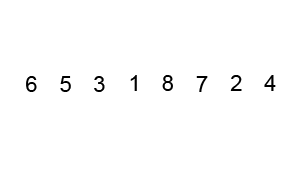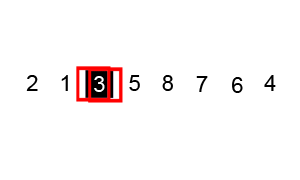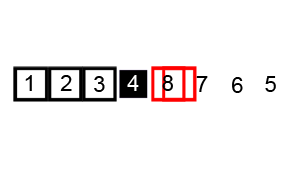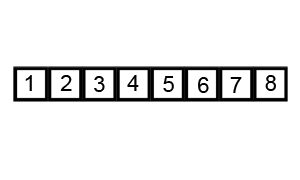
快速排序gif

代码实现

public void quickSort(int[] arr, int low, int high) {
    if (low < high) {
        int pi = partition(arr, low, high);

        quickSort(arr, low, pi - 1);
        quickSort(arr, pi + 1, high);
    }
}

private int partition(int[] arr, int low, int high) {
    int pivot = arr[high]; 
    int i = (low - 1);
    for (int j = low; j < high; j++) {
        if (arr[j] < pivot) {
            i++;
            int temp = arr[i];
            arr[i] = arr[j];
            arr[j] = temp;
        }
    }
    int temp = arr[i + 1];
    arr[i + 1] = arr[high];
    arr[high] = temp;
    
    return i + 1;
}

时间复杂度等分析

复杂度/稳定性	大O
最坏情况时间复杂度	O(n²)
最好情况时间复杂度	O(n log n)
平均时间复杂度	O(n log n)
空间复杂度	O(log n)
是否稳定	不稳定

归并排序

算法核心思想

归并排序是一种有效的排序算法，采用分治法（Divide and Conquer）的一个应用。它通过以下步骤实现：

分割：将原始数组分割成较小的数组，直到每个小数组只有一个位置
递归排序：递归地将小数组排序
合并：将排序后的小数组合并成较大的数组，直到最后只剩下一个完整的数组

通过这种方法，归并排序将大问题分解成小问题，然后解决这些小问题，最后将结果合并以解决原始问题

看下面这个动图示例：
归并排序gif

代码实现

public void mergeSort(int[] arr, int l, int r) {
    if (l < r) {
        int m = (l + r) / 2;

        mergeSort(arr, l, m);
        mergeSort(arr, m + 1, r);

        merge(arr, l, m, r);
    }
}

private void merge(int[] arr, int l, int m, int r) {
    // 创建临时数组
    int[] L = Arrays.copyOfRange(arr, l, m + 1);
    int[] R = Arrays.copyOfRange(arr, m + 1, r + 1);

    int i = 0, j = 0;
    int k = l;
    while (i < L.length && j < R.length) {
        if (L[i] <= R[j]) {
            arr[k] = L[i];
            i++;
        } else {
            arr[k] = R[j];
            j++;
        }
        k++;
    }

    // 复制剩余元素
    while (i < L.length) {
        arr[k] = L[i];
        i++;
        k++;
    }
    while (j < R.length) {
        arr[k] = R[j];
        j++;
        k++;
    }
}

时间复杂度等分析

复杂度/稳定性	大O
最坏情况时间复杂度	O(n log n)
最好情况时间复杂度	O(n log n)
平均时间复杂度	O(n log n)
空间复杂度	O(n)
是否稳定	稳定

堆排序

算法核心思想

利用了堆的特性来排序数组，具体步骤：

构建堆：将待排序的序列构造成一个大顶堆。选择堆顶元素：此时，整个序列的最大值就是堆顶的根节点
移除堆顶元素：将其与堆数组的末尾元素交换，此时末尾元素就是最大值
重新调整堆：将剩余的n-1个元素重新构造成一个堆，继续执行堆顶元素和末尾元素的交换，直到整个数组排序完成

看下面这个动图示例：
堆排序gif

代码实现

public class HeapSort {
    /**
     * 创建堆，
     * @param arr 待排序列
     */
    private static void heapSort(int[] arr) {
        //创建堆
        for (int i = (arr.length - 1) / 2; i >= 0; i--) {
            //从第一个非叶子结点从下至上，从右至左调整结构
            adjustHeap(arr, i, arr.length);
        }

        //调整堆结构+交换堆顶元素与末尾元素
        for (int i = arr.length - 1; i > 0; i--) {
            //将堆顶元素与末尾元素进行交换
            int temp = arr[i];
            arr[i] = arr[0];
            arr[0] = temp;

            //重新对堆进行调整
            adjustHeap(arr, 0, i);
        }
    }

    /**
     * 调整堆
     * @param arr 待排序列
     * @param parent 父节点
     * @param length 待排序列尾元素索引
     */
    private static void adjustHeap(int[] arr, int parent, int length) {
        //将temp作为父节点
        int temp = arr[parent];
        //左孩子
        int lChild = 2 * parent + 1;

        while (lChild < length) {
            //右孩子
            int rChild = lChild + 1;
            // 如果有右孩子结点，并且右孩子结点的值大于左孩子结点，则选取右孩子结点
            if (rChild < length && arr[lChild] < arr[rChild]) {
                lChild++;
            }

            // 如果父结点的值已经大于孩子结点的值，则直接结束
            if (temp >= arr[lChild]) {
                break;
            }

            // 把孩子结点的值赋给父结点
            arr[parent] = arr[lChild];

            //选取孩子结点的左孩子结点,继续向下筛选
            parent = lChild;
            lChild = 2 * lChild + 1;
        }
        arr[parent] = temp;
    }
}

时间复杂度等分析

复杂度/稳定性	大O
最坏情况时间复杂度	O(n log n)
最好情况时间复杂度	O(n log n)
平均时间复杂度	O(n log n)
空间复杂度	O(1)
是否稳定	不稳定

基数排序

算法核心思想

堆排序是基于堆的一种有效的排序方法。它利用了堆的特性来排序数组。

构建堆：将待排序的序列构造成一个大顶堆。选择堆顶元素：此时，整个序列的最大值就是堆顶的根节点
移除堆顶元素：将其与堆数组的末尾元素交换，此时末尾元素就是最大值
重新调整堆：将剩余的n-1个元素重新构造成一个堆，继续执行堆顶元素和末尾元素的交换，直到整个数组排序完成

看下面这个动图示例：
基数排序gif

代码实现

public class RadixSort {
    /**
     * 基数排序
     * @param arr 待排序数组
     */
    public static void radixSort(int[] arr) {
        int max = findMax(arr, arr.length);

        // 从个位开始，对数组arr按"指数"进行排序
        for (int exp = 1; max / exp > 0; exp *= 10) {
            countSort(arr, arr.length, exp);
        }
    }

    /**
     * 根据exp（10的倍数）进行计数排序
     */
    private static void countSort(int[] arr, int n, int exp) {
        int[] output = new int[n];
        int[] count = new int[10];

        // 存储计数
        for (int i = 0; i < n; i++) {
            count[(arr[i] / exp) % 10]++;
        }

        // 更改count，使其包含实际位置信息
        for (int i = 1; i < 10; i++) {
            count[i] += count[i - 1];
        }

        // 构建输出数组
        for (int i = n - 1; i >= 0; i--) {
            output[count[(arr[i] / exp) % 10] - 1] = arr[i];
            count[(arr[i] / exp) % 10]--;
        }

        // 将输出数组的内容复制到arr
        for (int i = 0; i < n; i++) {
            arr[i] = output[i];
        }
    }

    /**
     * 查找数组中的最大值
     */
    private static int findMax(int[] arr, int n) {
        int mx = arr[0];
        for (int i = 1; i < n; i++) {
            if (arr[i] > mx) {
                mx = arr[i];
            }
        }
        return mx;
    }
}

时间复杂度等分析

复杂度/稳定性	大O
最坏情况时间复杂度	O(nk)
最好情况时间复杂度	O(nk)
平均时间复杂度	O(nk)
空间复杂度	O(n + k)
是否稳定	稳定

计数排序

算法核心思想

计数排序是一种非比较型的排序算法，适用于一定范围内的整数排序。其基本步骤如下：

找出待排序的数组中最大和最小的元素。
统计数组中每个值为i的元素出现的次数，存入数组C的第i项。
对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）。
反向填充目标数组：将每个元素i放在新数组的第C[i]项，每放一个元素就将C[i]减去1。

看下面这个动图示例：
计数排序gif

代码实现

public class CountingSort {
    /**
     * 计数排序
     * @param arr 待排序数组
     */
    public static void countingSort(int[] arr) {
        // 找出数组中的最大和最小值
        int max = Arrays.stream(arr).max().getAsInt();
        int min = Arrays.stream(arr).min().getAsInt();

        // 计数数组
        int[] countArray = new int[max - min + 1];

        // 计数
        for (int i : arr) {
            countArray[i - min]++;
        }

        // 排序
        int index = 0;
        for (int i = 0; i < countArray.length; i++) {
            while (countArray[i] > 0) {
                arr[index++] = i + min;
                countArray[i]--;
            }
        }
    }
}

时间复杂度等分析

复杂度/稳定性	大O
最坏情况时间复杂度	O(n + k)
最好情况时间复杂度	O(n + k)
平均时间复杂度	O(n + k)
空间复杂度	O(n + k)
是否稳定	稳定

桶排序

算法核心思想

桶排序是一种分布式排序算法，适用于数据分布均匀的情况。其基本步骤如下：

创建桶：根据待排序数组的特点，确定桶的数量和范围。
分配数据：遍历数组，根据数据的特点分配到各个桶中。
排序桶内数据：对每个桶内的数据进行排序，可以使用任何排序方法。
合并桶：按顺序合并各个桶中的数据，形成最终的有序数组。

看下面这个动图示例：
桶排序gif

代码实现

public class CountingSort {
    /**
     * 计数排序
     * @param arr 待排序数组
     */
    public static void countingSort(int[] arr) {
        // 找出数组中的最大和最小值
        int max = Arrays.stream(arr).max().getAsInt();
        int min = Arrays.stream(arr).min().getAsInt();

        // 计数数组
        int[] countArray = new int[max - min + 1];

        // 计数
        for (int i : arr) {
            countArray[i - min]++;
        }

        // 排序
        int index = 0;
        for (int i = 0; i < countArray.length; i++) {
            while (countArray[i] > 0) {
                arr[index++] = i + min;
                countArray[i]--;
            }
        }
    }
}

时间复杂度等分析

复杂度/稳定性	大O
最坏情况时间复杂度	O(n²)
最好情况时间复杂度	O(n)
平均时间复杂度	O(n + k)
空间复杂度	O(n + k)
是否稳定	稳定