用PyMC3进行贝叶斯统计分析（代码+实例）

最新推荐文章于 2025-06-17 17:19:08 发布

Mr.Jcak

最新推荐文章于 2025-06-17 17:19:08 发布

阅读量3.9k

点赞数 3

CC 4.0 BY-SA版权

分类专栏： pymc3

本文链接：https://blog.youkuaiyun.com/weixin_38314865/article/details/97367566

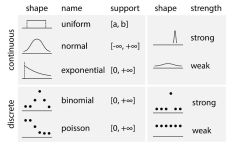
问题类型1：参数估计

真实值是否等于X？

给出数据，对于参数，可能的值的概率分布是多少？

例子1：抛硬币问题

硬币扔了n次，正面朝上是h次。

参数问题

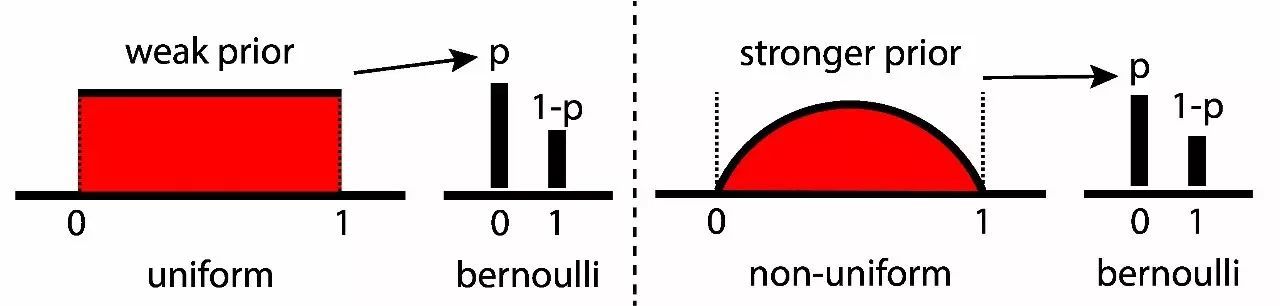
想知道 p 的可能性。给定 n 扔的次数和 h 正面朝上次数，p 的值很可能接近 0.5，比如说在 [0.48，0.52]？

说明

参数的先验信念：p∼Uniform(0,1)
似然函数：data∼Bernoulli(p)

import pymc3 as pm
import numpy.random as npr
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
from collections import Counter
import seaborn as sns

sns.set_style('white')
sns.set_context('poster')

%load_ext autoreload
%autoreload 2
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import warnings
warnings.filterwarnings('ignore')
from random import shuffle
total = 30
n_heads = 11
n_tails = total - n_heads
tosses = [1] * n_heads + [0] * n_tails
shuffle(tosses)

可视化数据：

def plot_coins():
    fig = plt.figure()
    ax = fig.add_subplot(1,1,1)
    ax.bar(list(Counter(tosses).keys()), list(Counter(tosses).values()))
    ax.set_xticks([0, 1])
    ax.set_xticklabels(['tails', 'heads'])
    ax.set_ylim(0, 20)
    ax.set_yticks(np.arange(0, 21, 5))        
    return fig

fig = plot_coins()
plt.show()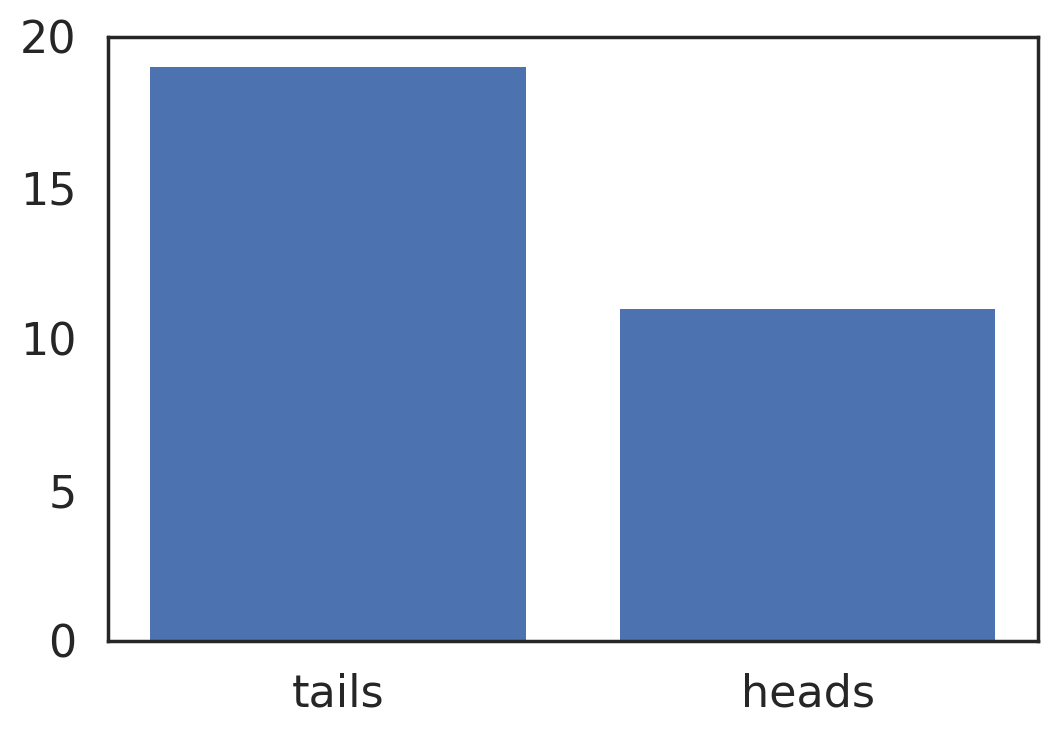

建立模型：

with pm.Model() as coin_model:
    # Specify prior using Uniform object.
    p_prior = pm.Uniform('p', 0, 1)  

    # Specify likelihood using Bernoulli object.
    like = pm.Bernoulli('