二连杆正/逆运动建模

[仿真环境]
matlab

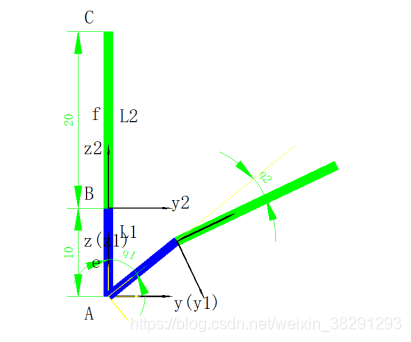
如图：二连杆由杆AB和杆BC组成，e,f为杆的重心位置，其中杆AB的长度为l2,杆BC的长度为l2。如图建立坐标系，坐标系y1oz1与杆AB固连，坐标系y2oz2与杆BC固连，即坐标系将跟着坐标系一起运动。将杆各自旋转一定角度，q1为杆AB的旋转角度，q2为杆BC旋转的角度，如图所示。将各点的位置以向量的形式表述。
首先定义基坐标系的轴向量为相互正交的单位向量：

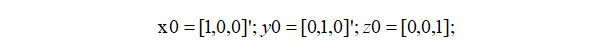
将旋转后的坐标系用基坐标系表达：（逆时针为正，顺时针为负）
坐标系x1y1z1

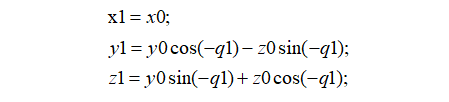
坐标系x2y2z1(相对于x1y1z1坐标系):

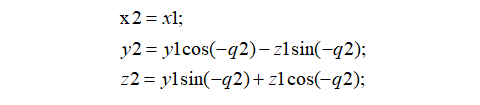
由上可得旋转矩阵：

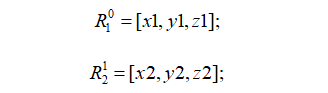
根据链式法则可得：

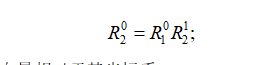
因此可以得到各点的位置向量相对于基坐标系：
P_A=[0,0,0];

P_B=P_A+l1Z1;
P_E=P_A+0.5l1Z1;
R_AB=P_B-P_A;
R_AE=P_E-P_A;
P_C=P_B+l2R01Z2;
P_F=P_B+0.5l2R01Z2
R_BC=P_C-P_B;
R_BF=P_F-P_B;
【正运动学解算】
转化为问题的形式来理解正运动学。
问题：已知：关节变量q1 q2，l1 ,l2;
求：末端的坐标C[CX,CY,CZ];

图中标注的角度q1,q2为标量

或
[CX,CY,CZ]=P_C;

【逆运动学解算】
转化为问题的形式来理解逆运动学。
问题：已知：末端的坐标C[CX,CY,CZ],l1 l2’
求：关节变量q1 q2，

方法一：（几何方法）

【仿真】

[下期预告]
二连杆动力学建模–自由的二连杆
[关注公众号获取源码和相关书籍资料]