逻辑回归模型logistic原理详解

Hello! 小A又来咯！

之前我们详细的介绍了使用线性回归模型来进行回归学习，那如果要做分类任务该怎么办呢？

考虑二分类任务，其输出值y属于集合[0,1]。而线性回归模型z=w^T*x+b是实值。为了进行分类任务，我们需要将实值z转化成[0,1]，我们首先想到的最理想的就是单位跃阶函数，即：

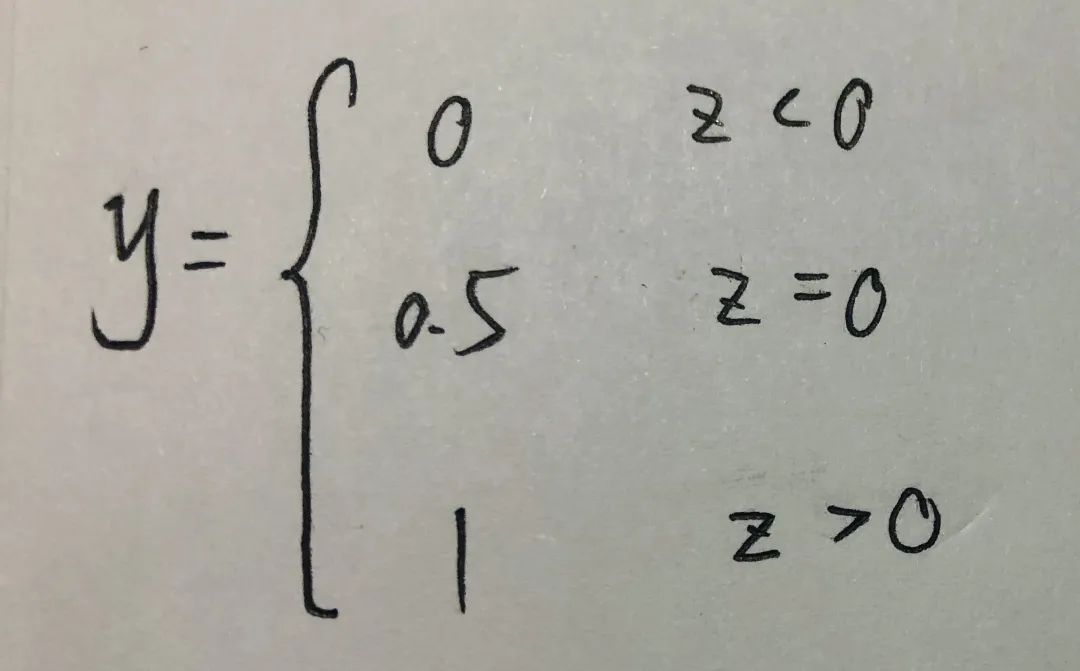
但是单位跃阶函数并不连续，并不能处处求导，不利于后续计算。所以我们需要找到一个能在一定程度上近似单位跃阶函数额替代函数，连续且单调可微。而对数几率函数正是这样的一个常用替代函数。如下图所示：

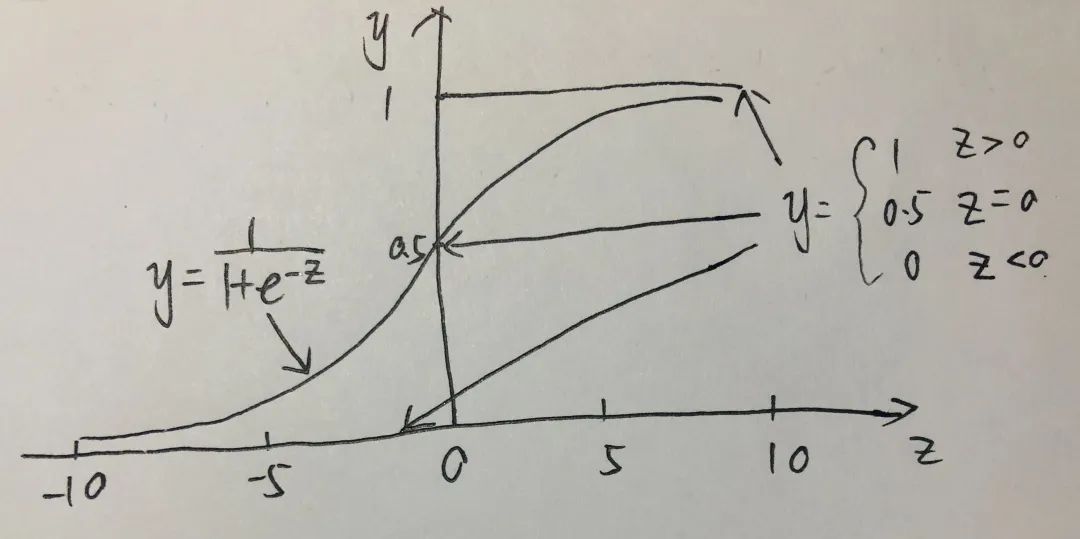
对数几率函数是一种sigmod函数。所谓sigmod函数就是形似“s”的函数，它可以将z值转化为一个接近0或1的y值。因此我们可以利用此单调可微函数将分类任务与线性回归模型联系起来，将z=w^T*x+b带入对数几率函数。可得：

我们可以看到此式实际上是用线性回归模型的预测结果去逼近真实标记的对数几率，进一步化简，可得