基于logistic回归原理和实现

Aphasla aphasia

已于 2023-12-03 00:42:05 修改

阅读量618

点赞数 6

文章标签：回归数据挖掘人工智能

于 2023-12-02 16:46:46 首次发布

本文链接：https://blog.youkuaiyun.com/m0_62682527/article/details/134753882

版权

本文详细介绍了Logistic回归的基本原理，包括线性模型的局限、sigmoid函数的应用、损失函数和梯度下降法的优化，以及如何在Python中使用sklearn库实现和调优。通过实例演示了鸢尾花数据集的处理和模型性能评估。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一、简介

Logistic回归是一种常用的分类算法，它被广泛应用于机器学习领域。与线性回归不同，Logistic回归用于解决二分类问题，通过将输入特征的线性组合映射到一个概率范围内来进行分类预测。在本文中，我们将介绍Logistic回归的原理并演示如何使用Python实现Logistic回归模型。

二、原理及其相关内容

2.1 线性模型

线性模型是机器学习中的一种基本模型，它基于线性关系来描述输入特征与输出之间的关系。在线性模型中，假设输入特征与输出之间存在一个线性函数关系，即输出可以通过输入的线性组合来表示。

表达式：

其中向量表达式：

其中线性模型的优点：

简单直观：线性模型的表达式简单明了，易于理解和解释。
计算高效：线性模型的训练和预测计算量较小，速度快，适用于大数据集和实时应用。
可解释性强：线性模型的特征权重可以解释为对输出的贡献程度，有助于分析特征的重要性和影响因素。
适用范围广：线性模型适用于各种机器学习任务，包括回归、分类、聚类等。

2.2 线性回归及其存在的问题

把线性回归用在二分类问题时，其中p属于类别的概率，可以表达为：

但是也存在不足：

1.等式两边的取值范围不同。

2.实际中有很多问题，都是当x很小或很大时，对于因变量p的影响很小，当x达到中间某个阈值时，影响很大。

2.3 logistic回归的引入

为了解决上述问题，可以采用logistic进行变换：

2.4 “S”型曲线

sigmoid函数是一种常用的非线性函数，其形状呈现S型曲线。它将输入的连续实数映射到一个范围在0到1之间的概率值。

表达式如下：

对于上述的进行变换，可以得到概率为0和概率为1的概率如下：

进而得到曲线：

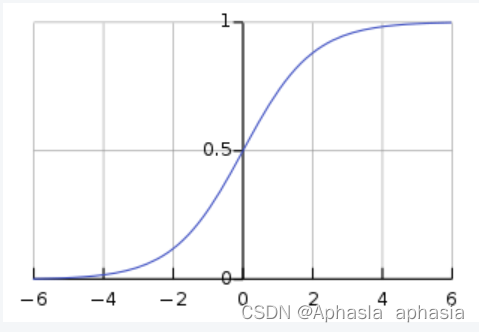
其中函数表达式：

2.5 损失函数和似然函数

Logistic回归在线性回归的输出y上引入损失函数g（z）：

似然函数：

对于二分类问题，其中假设：

2.6 梯度下降法

是一种优化算法，用于在机器学习和优化问题中寻找目标函数的最小值或最大值。

梯度下降法的基本思想是通过迭代的方式不断调整参数，使得目标函数在参数空间中逐渐朝着梯度下降的方向更新，直到达到极小值或满足停止条件为止。具体而言，梯度下降法利用目标函数的梯度信息来指导参数的更新方向和步长。

具体实现如下：

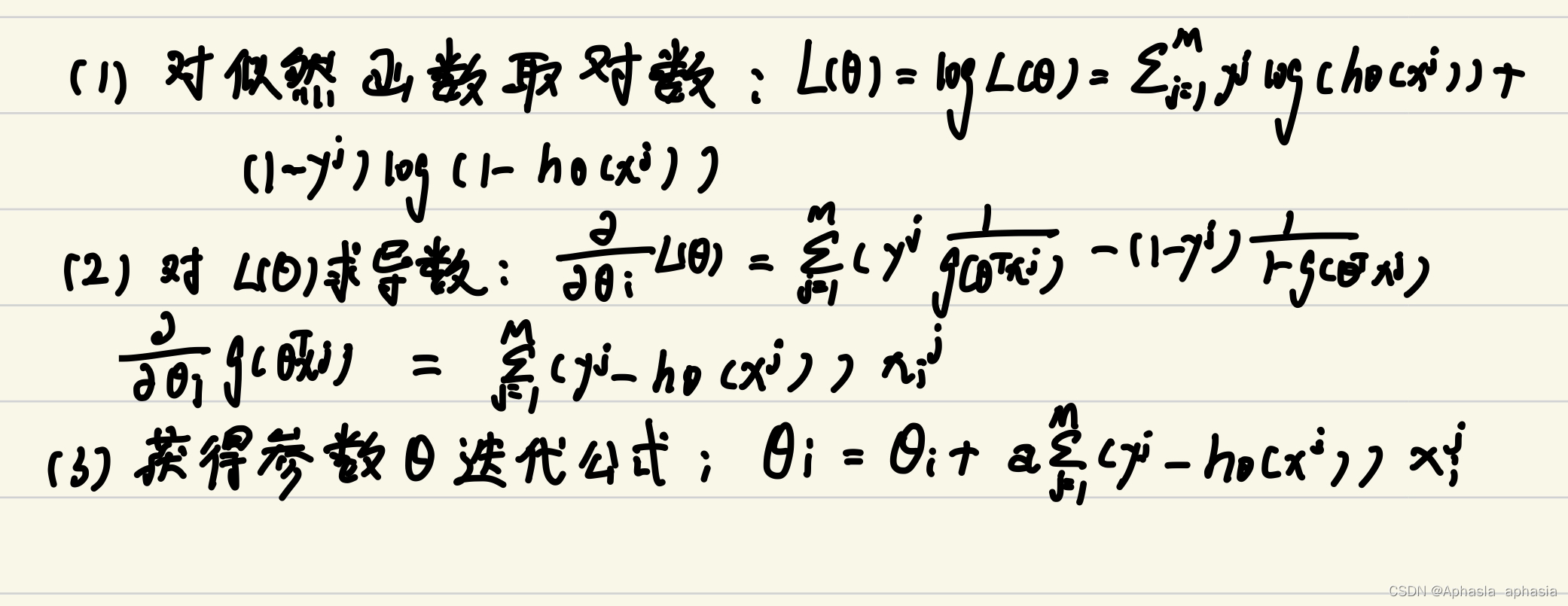
三、python的代码实现

3.1数据的读取

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

# 加载鸢尾花数据集
iris = datasets.load_iris()
X = iris.data
y = (iris.target == 0).astype(int)  # 仅使用第一类鸢尾花进行演示

3.2 添加到偏置矩阵中并定义函数

# 添加偏置项到特征矩阵中
X = np.hstack((np.ones((X.shape[0], 1)), X))

# 定义sigmoid函数
def sigmoid(x):
    return 1 / (1 + np.exp(-np.clip(x, -15, 15)))

3.3 梯度上升算法和改进后的随机梯度上升算法

# 梯度上升算法实现Logistic回归
def logistic_regression_gradient_ascent(X, y, num_steps, learning_rate):
    weights = np.zeros(X.shape[1])  # 初始化权重
    likelihoods = []  # 存储每次迭代的最大似然函数值
    for step in range(num_steps):
        scores = np.dot(X, weights)
        predictions = sigmoid(scores)

        # 计算梯度
        output_error = y - predictions
        gradient = np.dot(X.T, output_error)

        # 更新权重
        weights += learning_rate * gradient

        # 计算最大似然函数值
        likelihood = np.sum(y * np.log(predictions + 1e-15) + (1 - y) * np.log(1 - predictions + 1e-15))
        likelihoods.append(likelihood)

    return weights, likelihoods

# 改进的随机梯度算法实现Logistic回归
def logistic_regression_stochastic_gradient(X, y, num_epochs, learning_rate):
    weights = np.zeros(X.shape[1])  # 初始化权重
    likelihoods = []  # 存储每次迭代的最大似然函数值
    for epoch in range(num_epochs):
        for i in range(X.shape[0]):
            scores = np.dot(X[i], weights)
            prediction = sigmoid(scores)

            # 计算梯度
            output_error = y[i] - prediction
            gradient = X[i] * output_error

            # 更新权重
            weights += learning_rate * gradient

            # 计算最大似然函数值
            likelihood = np.sum(y * np.log(prediction + 1e-15) + (1 - y) * np.log(1 - prediction + 1e-15))
            likelihoods.append(likelihood)

    return weights, likelihoods

3.4 准确率的计算

# 准确率
def predict(X, weights):
    scores = np.dot(X, weights)
    predictions = sigmoid(scores)
    return (predictions >= 0.5).astype(int)

3.5 测试和训练集并且可视化输出

# 梯度上升算法训练Logistic回归模型
num_steps = 1000
learning_rate = 0.1
weights_gradient_ascent, likelihoods_gradient_ascent = logistic_regression_gradient_ascent(X, y, num_steps, learning_rate)

# 改进的随机梯度算法训练Logistic回归模型
num_epochs = 100
learning_rate = 0.1
weights_stochastic_gradient, likelihoods_stochastic_gradient = logistic_regression_stochastic_gradient(X, y, num_epochs, learning_rate)

# 可视化结果
plt.scatter(X[y == 1][:, 1], X[y == 1][:, 2], color='b', label='Iris-setosa')
plt.scatter(X[y == 0][:, 1], X[y == 0][:, 2], color='r', label='Others')

x_axis = np.linspace(4, 8, 10)

# 梯度上升算法的最佳拟合直线
y_axis_gradient_ascent = -(weights_gradient_ascent[0] + weights_gradient_ascent[1]*x_axis) / weights_gradient_ascent[2]
plt.plot(x_axis, y_axis_gradient_ascent, color='g', linestyle='-', label='Gradient Ascent')

# 改进的随机梯度算法的最佳拟合直线
y_axis_stochastic_gradient = -(weights_stochastic_gradient[0] + weights_stochastic_gradient[1]*x_axis) / weights_stochastic_gradient[2]
plt.plot(x_axis, y_axis_stochastic_gradient, color='m', linestyle='--', label='Stochastic Gradient')

plt.xlabel('Sepal Length')
plt.ylabel('Sepal Width')
plt.legend()
plt.show()

# 输出最大似然函数的值
print("梯度上升算法的最大似然函数值:", likelihoods_gradient_ascent[-1])
print("改进的随机梯度算法的最大似然函数值:", likelihoods_stochastic_gradient[-1])


# 在训练集上进行预测
y_pred_gradient_ascent = predict(X, weights_gradient_ascent)
accuracy_gradient_ascent = np.mean(y_pred_gradient_ascent == y)
print("梯度上升算法的准确率:", accuracy_gradient_ascent)

y_pred_stochastic_gradient = predict(X, weights_stochastic_gradient)
accuracy_stochastic_gradient = np.mean(y_pred_stochastic_gradient == y)
print("改进的随机梯度算法的准确率:", accuracy_stochastic_gradient)

输出结果：