数学基础-核技巧

一、非线性分类问题

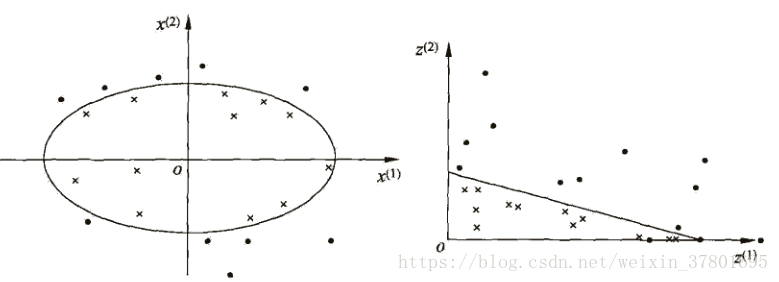
非线性分类问题指通过非线性模型才能很好的分类的问题，如下图所示，用直线无法将左图的两个类别分类，需要用椭圆，那么椭圆表示式为分类模型，该分类模型为非线性分类模型。将原空间X通过映射函数映射到Z空间，$z=\Phi (x)$，通过一个非线性变换，将源空间映射到特征空间，特征空间的特征是线性可分的，在特征空间求解线性模型。

二、核技巧

核技巧的思想是只定义核函数$K(x,y)=\Phi (x)\ast \Phi (y)$，而不显示的定义映射函数$\Phi (x)$，因为直接计算$K(x,y)$ 较寻找映射函数容易，因为特征空间和映射函数并不唯一。同一核函数可以分解为不同的映射函数

核函数方法的广泛应用，与其特点是分不开的：
（1）核函数的引入避免了“维数灾难”，大大减小了计算量。而输入空间的维数n对核函数矩阵无影响，因此，核函数方法可以有效处理高维输入。
（2）无需知道非线性变换函数Φ的形式和参数.
（3）核函数的形式和参数的变化会隐式地改变从输入空间到特征空间的映射，进而对特征空间的性质产生影响，最终改变各种核函数方法的性能。
（4）核函数方法可以和不同的算法相结合，形成多种不同的基于核函数技术的方法，且这两部分的设计可以单独进行，并可以为不同的应用选择不同的核函数和算法。

三、常用的核函数

1、多项核函数
$K(x,y)=(x\ast y+1{)}^p$
2、高斯核函数
$K(x,y)=exp(-\frac{||x-y|{|}^2}{2{\sigma }^2})$
3、径向基核函数
$K(x,y)=exp(-\gamma ||x-y|{|}^2)$
4、sigmoid核函数
$K(x,y)=tanh(\eta <x{}_i,x>+\theta )$

四、核技巧的应用

1、非线性支持向量机（KSVM）
选择核函数，支持向量机的策略目标函数为

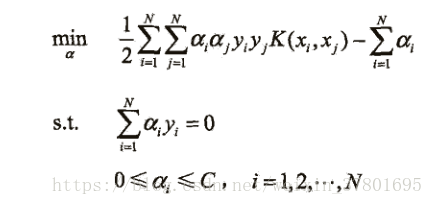
求解上述函数为求凸二次规划问题
决策函数为

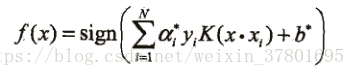
2、核PCA（KPCA）

核PCA是在降维的过程中，将源数据进行映射，对变换过程中出现的$\Phi (x)\ast \Phi (y)$ 用$K(x,y)$ 替换。

写博客的目的是学习的总结和知识的共享，如有侵权，请与我联系，我将尽快处理
参考
李航的《统计机器学习》
http://songcy.net/posts/story-of-basis-and-kernel-part-1/
http://songcy.net/posts/story-of-basis-and-kernel-part-2/