统计学习方法——（第八章）提升方法详解及推导

一、：知识梳理

参考链接1：https://www.cnblogs.com/liaohuiqiang/p/10980080.html

参考链接2：https://blog.youkuaiyun.com/lianjixuexi/article/details/78972594

二、提升方法

1、原理

提升方法（boosting）是一种常用的统计学习方法，应用广泛且有效。在分类问题中，它通过改变训练样本的权重，学习多个分类器，并将这些分类器进行线性组合，提高分类的性能。说白了就是结合多个分类器，进而提高分类精度。

boosting基于这样一种思想：对于一个复杂任务来说，将多个专家的判断进行适当的综合所得出的判断，要比其中任何一个专家单独的判断好。实际上就是“三个臭皮匠，顶个诸葛亮”的道理。

2、相关概念

强可学习：在概率近似正确（probably approximately correct，PAC）学习的框架中，一个概念，如果存在一个多项式的学习算法能够学习它，并且正确率很高，那么称这个概念是强可学习的。

弱可学习：一个概念，如果存在一个多项式的学习算法能够学习它，学习的正确率仅比随机猜测略好，那么称为弱可学习的。

强可学习和弱可学习：Schapire证明了强可学习与弱可学习是等价的，也就是说，在PAC学习的框架下，一个概念是强可学习的充要条件是这个概念是弱可学习的。

从弱学习到强学习：可将“弱学习”提升为“强学习”，弱学习算法通常比强学习算法容易得多。具体如何实施提升，便称为开发提升方法时要解决的问题。有很多提升算法被提出，最具代表性的就是AdaBoost。

训练误差：

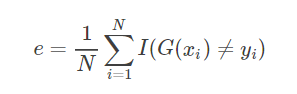
 训练误差率：算法是有样本的权值的，主要更新样本权值，在更新分类器权值

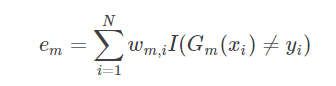
3、模型

1）思路：

提升方法就是从弱学习算法出发，反复学习，得到一系列弱分类器（又称为基分类器），然后组合这些弱分类器，构成一个强分类器。大多数的提升方法都是改变训练数据的概率分布（训练数据的权重分布），针对不同的训练数据分布，调用弱学习算法学习一系列弱分类器。这里就有两个问题。

2）AdaBoost算法：（主要更新样本权值，在更新分类器权值）

输入：训练数据集T=(x1，y1)，(x2，y2),...,(xN,yN)T=(x1，y1)，...,(xN，yN)，其中xi∈X⊆Rn，yi∈{−1,+1}，xi⊆Rn，yi∈{−1，+1}。

 

输出：最终分类器G(x)

（1）初始化训练数据的权值分布

这里假设了数据具有均匀的权值分布，每个样本在基分类器的学习作用相同。

（2）进行m=1,2,...,M轮训练，根据分类误差率求解分类器占总分类器的权重

(a) 用权值分布为Dm的训练数据学习，得到基分类器Gm(x):X→{+1,−1}

(b) 计算Gm(x)在训练集上的分类误差率

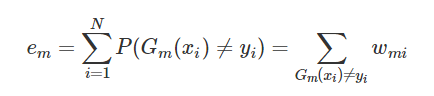
m表示第m轮，i表示第i个实例。这表明，Gm(x)在加权的训练集上的分类误差率是被Gm(x)误分类样本的权重之和。

(c) 计算Gm(x)的系数αm。

αm表示Gm(x)在最终分类器中的重要性。由此可知，当em⩽0.5，αm⩾0，而且αm随着em的减小而增大。因此，分类误差越小的基分类器在最终分类器中的作用越大。

(d) 更新训练集的权值分布，为下一轮做准备

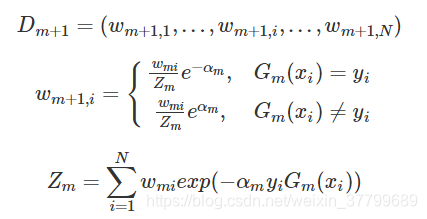
其中Zm为规范化因子。误分类样本权值变大，正确分类样本权值缩小，两相比较放大了1−em/em倍。

（3）构建基分类器的线性组合，注意αm之和不为1。

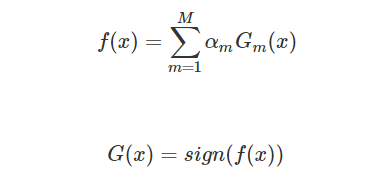
三、AdaBoost算法的训练误差分析

1、为什么要进行误差分析？

书中所说，训练误差率不断减少是AdaBoost具有应用价值的前提。那为什么训练误差不断减少呢？这需要进行误差分析，来证明训练误差不断减少。

同时，训练误差是不断减少的，那么训练误差也在学习过程中不断地减少（注意是学习过程中分类器的加法模型的训练误差一直减少，而后一个分类器的训练误差不一定比前一个分类误差的训练误差小）。

2、AdaBoost的训练误差界

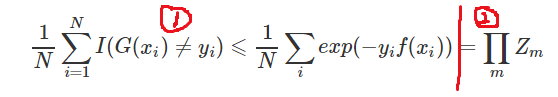
3、第1部分推导

因为满足I(G(xi)!=yi)，所以已知G(xi)不等于yi。根据已知有

代入指数公式有下式，得证

4、第2部分推导 

首先，根据左式红圈得到右式。（直接做个变形比较简单不解释）

                             

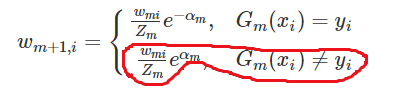
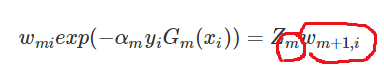
 推导：

总结：这一定理说明，误差是由下界，并且不断减少。因此，可以在每一轮选取恰当的Gm使得Zm最小，从而使训练误差下降最快。 

四、 二分类问题AdaBoost的训练误差界

问题：

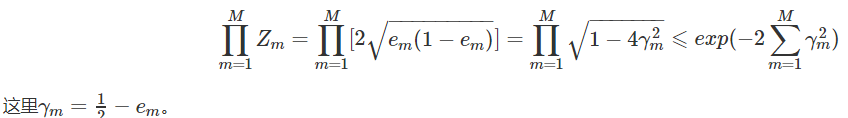
证明等式部分： 

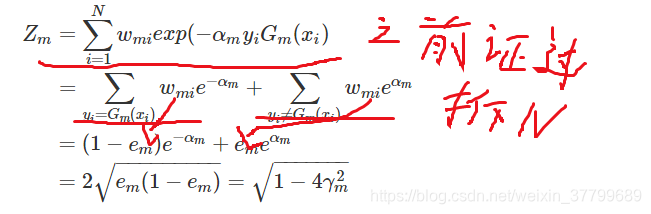
再证不等式部分：

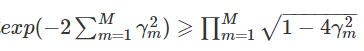
 对指数进行泰勒展开

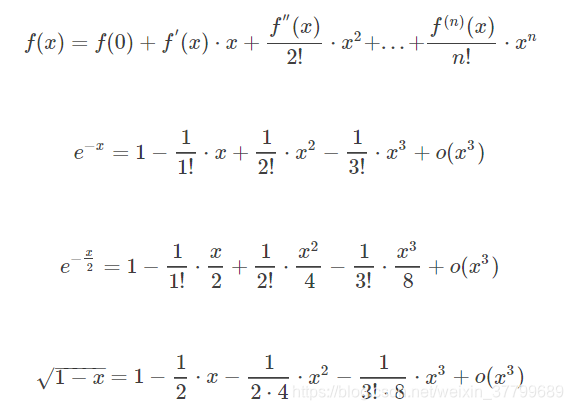
推论：

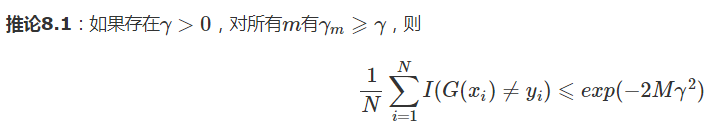
这表明在此条件下AdaBoost的训练误差是以指数速率下降的，即每次的误差都小于上一个误差的指数，这一性质当然很有吸引力。与一些早期的提升方法不同，AdaBoost具有适应性，即它能适应弱分类器各自的训练误差率。这也是它名称的由来，Ada是Adaptive的简写。

五、前向分布算法角度解释AdaBoost

1、前向分布算法

加法模型：其中b为基函数，γm为基函数的参数，βm为基函数的系数。

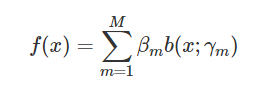
在给定训练集和损失函数L(y,f(x))L(y,f(x))的条件下，学习加法模型f(x)f(x)成为经验风险极小化即损失函数极小化问题：

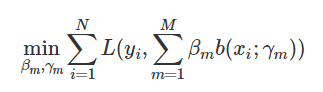
前向分步算法求解这一优化问题的想法是：从前向后，每一步只学习一个基函数及其系数，逐步逼近优化目标函数式，那么就可以简化优化的复杂度。每步优化如下损失：

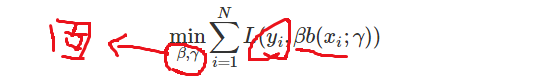
2、前向分布算法与AdaBoost 

1）结论

可认为AdaBoost是模型为加法模型，损失函数为指数函数，学习算法为前向分步算法时的二分类学习方法。由前向分步算法可以推导出AdaBoost，用定理叙述这一关系。AdaBoost算法是前向分步加法算法的特例。这时，模型是由基本分类器组成的加法模型，损失函数是指数函数。

2）问题

3）证明：前向分步算法的损失函数是指数损失函数

        

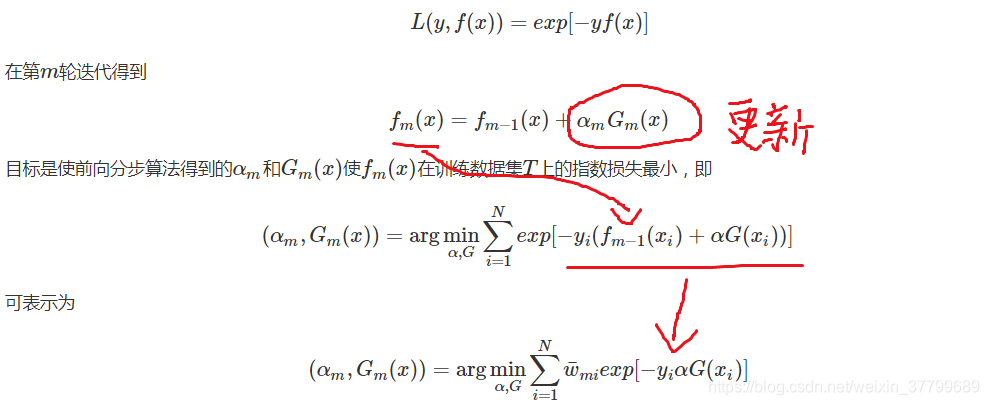
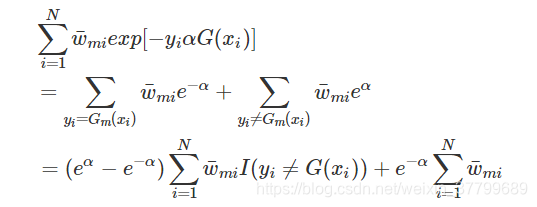
4）证明：更新值相同，这与AdaBoost算法第2(d)步的样本权值更新，只差规范化因子，因而等价。

 六、 从提升树到GBDT

1、提升树

提升树是AdaBoost的特例，可以认为提升树是基本分类器为二类分类树，损失函数为平方损失函数的AdaBoost。分类问题的提升树改变权重，回归问题的提升树拟合残差。

因为损失函数是平方损失函数的时候，残差是好求的，而如果不是平方损失函数也不是指数损失函数的时候，残差就不可求得，这时，就要用损失函数关于当前模型f（x）的负梯度来近似代替残差。梯度提升算法就是用梯度下降法来讲弱分类器提升为强分类器的算法。

2、GBDT

使用梯度提升进行分类的算法叫做GBDT，进行回归时则叫做GBRT。一般的提升树是用残差来确定树的叶节点的切分，并根据残差来确定该切分下的输出值，而GBDT首先是根据负梯度来确定切分，确定切分后根据线性搜索估计叶节点区域的值，使损失函数极小化。

3、提升树和AdaBoost

AdaBoost是提升思想的算法模型,经典的AdaBoost一般用于分类问题，并没有指定基函数，或者说是基分类器，它可以从改变样本的权值的角度和前向分布算法的角度来解释。当确定基函数是回归或分类树时，结合前向分布算法就得出提升树算法。 

4、GBDT流程

1）初始化,初始化一个常数值，即只有一个根节点的树

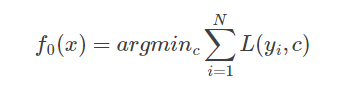
2） 进行m=1,2,...,M轮训练，根据分类误差率求解分类器占总分类器的权重

(a)for i=1,2,…,N,计算负梯度（伪残差）：

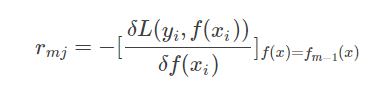
(b)对伪残差拟合一个回归树，得到第m棵树的叶结点区域 （这里的J是事先确定的，也就是把区域分成的份数，确定份数后穷举所有切分拟合残差得出损失误差最小的切分就是最佳切分，从而就可以得出第m棵树的叶结点区域）

(c)对j=1,2,..J,计算

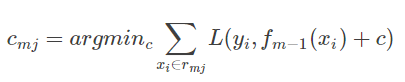
(d)更新并输出最终模型

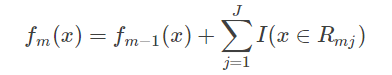
5、梯度提升 

提升树利用加法模型与前向分步算法实现学习的优化过程。当损失函数是平方损失和指数损失时，每一步优化是简单的。但对一般损失函数而言，往往每一步优化并不容易。针对这一问题，Freidman提出了梯度提升（gradient boosting）算法。这是利用最速下降法的近似方法，其关键是利用损失函数的负梯度在当前模型的值。

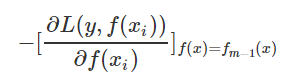
作为回归问题提升树算法中残差的近似值，拟合一个回归树