模型基本原理
采用加法模型和前向分步算法,以决策树为基函数的算法被称为提升树,由如下公式表示,其中 T ( x ; θ M ) T(x;\theta _M) T(x;θM)表示决策树, θ M \theta_M θM表示决策树的参数,M为树的个数。
f M ( x ) = ∑ m = 1 M T ( x ; θ M ) f_M(x)=\sum_{m=1}^{M}T(x;\theta _M) fM(x)=m=1∑MT(x;θM)
回归核心思想
首先确定初始提升树 f 0 ( x ) = 0 f_0(x)=0 f0(x)=0, 第m步的模型如下,
f m ( x ) = f m − 1 ( x ) + T ( x ; θ m ) f_m(x)=f_{m-1}(x)+T(x;\theta_m) fm(x)=fm−1(x)+T(x;θm)
确定下一棵决策树参数的方法如下,
θ m ^ = a r g m i n θ m ∑ i = 1 N L ( y i , f m − 1 ( x i ) + T ( x i ; θ m ) ) \hat{\theta _m}=argmin_{\theta _m}\sum_{i=1}^{N}L(y_i, f_{m-1}(x_i)+T(x_i;\theta_ m)) θm^=argminθmi=1∑NL(yi,fm−1(xi)+T(xi;θm))
通过找到合适的参数,从而得到合适的提升树模型,而采用何种损失函数便成为提升树学习算法的核心内容。对于回归问题的提升树,某棵树对于某个样本 x j x_j xj的预测值如下,J为这棵树叶子节点个数,具体如何理解,请见决策树的解释。
T
(
x
;
θ
)
=
∑
j
=
1
J
c
j
I
(
x
∈
R
j
)
T(x;\theta)=\sum_{j=1}^{J}c_j I(x\in R_j)
T(x;θ)=j=1∑JcjI(x∈Rj)
每棵树构建好之后对于前向分步算法的应用如下,
{
f
0
(
x
)
=
0
f
m
(
x
)
=
f
m
−
1
(
x
)
+
T
(
x
;
θ
m
)
m
=
1
,
2
,
.
.
.
,
M
f
M
(
x
)
=
∑
m
=
1
M
T
(
x
;
θ
m
)
\left\{\begin{matrix} f_0(x)=0\\ f_m(x)=f_{m-1}(x)+T(x;\theta _m) \quad m=1,2,...,M\\ f_M(x)=\sum_{m=1}^{M}T(x;\theta _m) \end{matrix}\right.
⎩⎨⎧f0(x)=0fm(x)=fm−1(x)+T(x;θm)m=1,2,...,MfM(x)=∑m=1MT(x;θm)
第m步中,给定
f
m
−
1
(
x
)
f_{m-1}(x)
fm−1(x),需求解如下公式得到
θ
m
^
\hat{\theta _m}
θm^,
θ
m
^
=
a
r
g
m
i
n
θ
m
∑
i
=
1
N
L
(
y
i
,
f
m
−
1
(
x
i
)
+
T
(
x
i
;
θ
m
)
)
\hat{\theta _m}=argmin_{\theta _m}\sum_{i=1}^{N}L(y_i, f_{m-1}(x_i)+T(x_i;\theta_ m))
θm^=argminθmi=1∑NL(yi,fm−1(xi)+T(xi;θm))
如果采用平方差损失函数,
L
(
y
,
f
(
x
)
)
=
(
y
−
f
(
x
)
)
2
L(y,f(x))=(y-f(x))^2
L(y,f(x))=(y−f(x))2
其损失变为如下公式,这里
r
=
y
−
f
m
−
1
(
x
)
r=y-f_{m-1}(x)
r=y−fm−1(x),表示模型拟合的是数据的残差。
L ( y , f m − 1 ( x ) + T ( x ; θ m ) ) = [ y − f m − 1 ( x ) − T ( x ; θ m ) ] 2 = [ r − T ( x ; θ m ) ] 2 L(y,f_{m-1}(x)+T(x;\theta_m))= [y-f_{m-1}(x)-T(x;\theta_m)]^2= [r-T(x;\theta_m)]^2 L(y,fm−1(x)+T(x;θm))=[y−fm−1(x)−T(x;θm)]2=[r−T(x;θm)]2
梯度提升
上述算法求解的核心在于对于模型的损失函数是平方损失的,求解很简单,但是对于一般的损失函数来说,每一步的优化并不是很容易,因而把损失函数的负梯度值作为每个阶段回归的目标去拟合一棵回归树才是一个比较理想的选择,负梯度公式如下,
r m i = − [ ∂ L ( y , f ( x ) ) ∂ f ( x ) ] f ( x ) = f m − 1 ( x ) r_{mi}=-\left [ \frac{\partial L(y,f(x))}{\partial f(x)}\right ]_{f(x)=f_{m-1}(x)} rmi=−[∂f(x)∂L(y,f(x))]f(x)=fm−1(x)
上述算法计算梯度的过程叫做有一个问题,如果基学习器太少,容易导致跨越最优解的情况,在最速下降法中不可避免的会利用到学习率,这里也可采用添加学习率的方法,增大提升树中基学习器的数量来提升性能,
f
m
(
x
)
=
f
m
−
1
(
x
)
+
ν
⋅
h
m
(
x
)
,
0
<
ν
≤
1
f_m(x) = f_{m-1}(x) + \nu \cdot h_m(x), \quad 0 < \nu \leq 1
fm(x)=fm−1(x)+ν⋅hm(x),0<ν≤1
上式的
ν
\nu
ν即是上文提到的学习率,学习率越小,提升树中基学习器的数量会变多,从而更加精细的逼近最优解,其缺点很明显,收敛比较慢,但不会发生震荡,这里举一个比较通俗易懂的例子来加深理解。
可以假设一个场景,如果你要走一条路,到达终点,但是你并不知道终点的具体方向在哪,首先你需要选择一共要走多少步,确定走多少步的过程就是确定学习率的过程,而后开始走第一步,在走第一步的时候有个高人告诉你终点大概方向是什么样的,这即是梯度方向,且第一步走多大最合适,这是梯度的大小,这个时候你就根据这个高人的指点走出重要的一步而后再去询问那个高人,高人又会指一条明路,而后一直重复上述过程,直到走到终点。还是上面的那个例子,如果每步走的太大,就有可能出现走过了的风险,那么这个时候就看出来步子小的好处了,步子小不怕,多走几步就是了,这样就没有上述提到的风险了。
分类核心思想
二分类
分类问题是回归问题的变形,与回归问题不同的一点是分类问题用到的损失函数是对数损失函数(logistic loss), 下面是对对数损失函数的解释。
对于二项分布, y ∗ ∈ { 0 , 1 } y^*\in \{0,1\} y∗∈{0,1}, 定义预测概率为 p ( x ) = P ( y ∗ = 1 ) p(x)=P(y^*=1) p(x)=P(y∗=1), 而损失函数可定义如下所示,
L
(
y
∗
,
p
(
x
)
)
=
{
−
l
o
g
(
p
(
x
)
)
,
i
f
y
∗
=
1
−
l
o
g
(
1
−
p
(
x
)
)
,
i
f
y
∗
=
0
L(y^*,p(x))=\left\{\begin{matrix} -log(p(x)), \quad if \quad y^*=1\\ -log(1-p(x)), \quad if \quad y^*=0 \end{matrix}\right.
L(y∗,p(x))={−log(p(x)),ify∗=1−log(1−p(x)),ify∗=0
合并起来写为如下公式,之后的算法和gbdt回归树的思想大同小异。
L ( y ∗ , p ( x ) ) = − y l o g ( p ( x ) ) − ( 1 − y ) l o g ( 1 − p ( x ) ) L(y^*, p(x))=-ylog(p(x))-(1-y)log(1-p(x)) L(y∗,p(x))=−ylog(p(x))−(1−y)log(1−p(x))
多分类
在多分类问题中,假设有k个类别,那么每一轮迭代实质是构建了k棵树,对某个样本x的预测值为
f 1 ( x ) , f 2 ( x ) , . . . , f k ( x ) f_1(x), f_2(x),...,f_k(x) f1(x),f2(x),...,fk(x)
在这里我们仿照多分类的逻辑回归,使用softmax来产生概率,
p c = e x p ( f c ( x ) ) / ∑ i = 1 k e x p ( f i ( x ) ) p_c=exp(f_c(x))/\sum_{i=1}^{k}exp(f_i(x)) pc=exp(fc(x))/i=1∑kexp(fi(x))
而后在计算损失时采用的依然是对数损失函数,并对 f 1... f k f1...fk f1...fk都可以算出一个梯度, f 1... f k f1...fk f1...fk便可以计算出当前轮的残差,供下一轮迭代学习。最终做预测时,输入的x会得到k个输出值,然后通过softmax获得其属于各类别的概率即可,每个阶段对于k棵数,总共m个阶段,树的总数为 k ∗ m k*m k∗m。
拓展之细节
1. 梯度提升 VS adaboost
adaboost和GBDT的相同之处:gbdt计算残差这一步相当于给每个样本赋予权重,因为一轮内计算的残差绝对值越大,负梯度的方向会整体更偏向它的方向,相当于回归任务更偏向于它这一方,这样才能让这个残差较大的预测结果和真实值更加正确,这样才能够保证整体的误差最小,这样间接的就给每个样本赋予权重了,残差越大,赋予的权重就越大。
2. 样本选择 subsample
提升树中每个基学习器的训练样本是整体训练样本的一部分,subsample参数决定了这个比例,这提高了模型的泛化能力,有效防止过拟合。注意这里的子采样和随机森林不一样,随机森林使用的是放回抽样,而这里是不放回抽样,即一次从原始数据中取出一部分数据进行训练。如果取值为1,则全部样本都使用,等于没有使用子采样。如果取值小于1,则只有一部分样本会去做GBDT的基学习器拟合。选择小于1的比例可以减少方差,即防止过拟合,但是会增加样本拟合的偏差,因此取值不能太低。推荐在[0.5,0.8]之间,默认是1.0,即不使用子采样,
3. 梯度提升 VS 决策树
提升树模型效果好的核心在于每棵树都能够找到当前全局最优解,且每棵树的最优解都更加逼近真实解,而决策树只有一次机会逼近全局最优解,那就是在根节点选择特征时,因而这样建立的模型有过拟合的风险,下面的例子就能够很好地解释这一点。
假设我们现在有一个训练集,训练集只有4个人,A,B,C,D,他们的年龄分别是14,16,24,26。其中A、B分别是高一和高三学生;C,D分别是应届毕业生和工作两年的员工。如果是用一棵传统的回归决策树来训练,会得到如下图所示。
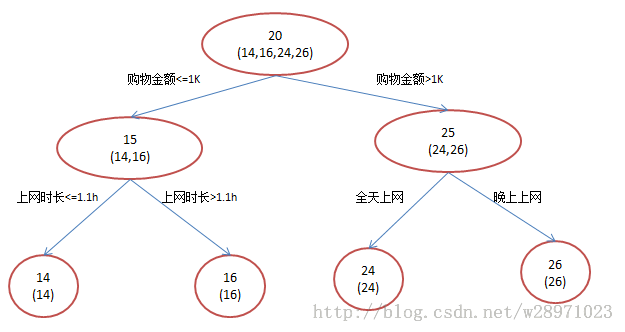
现在我们使用GBDT来做这件事,由于数据太少,我们限定叶子节点最多有两个,即每棵树都只有一个分枝,并且限定只学两棵树,我们会得到如下图所示结果。
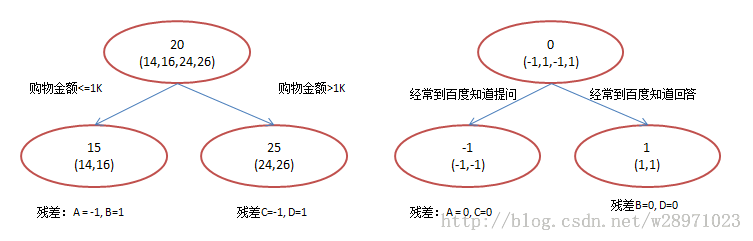
在第一棵树分枝和图1一样,由于A,B年龄较为相近,C,D年龄较为相近,他们被分为两拨,每拨用平均年龄作为预测值。此时计算残差,所以A的残差就是14-15=-1(注意,A的预测值是指前面所有树累加的和,这里前面只有一棵树所以直接是15,如果还有树则需要都累加起来作为A的预测值)。进而得到A,B,C,D的残差分别为-1,1,-1,1。然后我们拿残差替代A,B,C,D的原值,到第二棵树去学习,如果我们的预测值和它们的残差相等,则只需把第二棵树的结论累加到第一棵树上就能得到真实年龄了。这里的数据显然是我可以做的,第二棵树只有两个值1和-1,直接分成两个节点。此时所有人的残差都是0,即每个人都得到了真实的预测值。
最后GBDT的预测结果为:
A: 14岁高一学生,购物较少,经常问学长问题;预测年龄A = 15 – 1 = 14;
B: 16岁高三学生;购物较少,经常被学弟问问题;预测年龄B = 15 + 1 = 16;
C: 24岁应届毕业生;购物较多,经常问师兄问题;预测年龄C = 25 – 1 = 24;
D: 26岁工作两年员工;购物较多,经常被师弟问问题;预测年龄D = 25 + 1 = 26。
那么哪里体现了Gradient呢?其实回到第一棵树结束时想一想,无论此时的cost function是什么,是均方差还是均差,只要它以误差作为衡量标准,残差向量(-1, 1, -1, 1)都是它的全局最优方向,这就是Gradient。而且GBDT同随机森林一样,不容易陷入过拟合,而且能够得到很高的精度。
gbdt vs random_forest
- rf每次迭代的样本是从全部训练集中有放回抽样形成的,而GBDT每次使用全部样本
- gbdt对异常值比rf更加敏感
- gbdt是串行,rf是并行
- gbdt是提高降低偏差提高性能,rf是通过降低方差提高性能
- gbdt对输出值是进行加权求和,rf对输出值是进行投票或者平均
有放回采样和无放回采样
有放回采样:天生会有
63.2
%
63.2\%
63.2%的数据采集不到,rf中每一棵树的采样就是有放回采样。
无放回采样:随机的对全集采样,每个样本都有可能被采到,这种采样是全局的。
























 873
873

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








