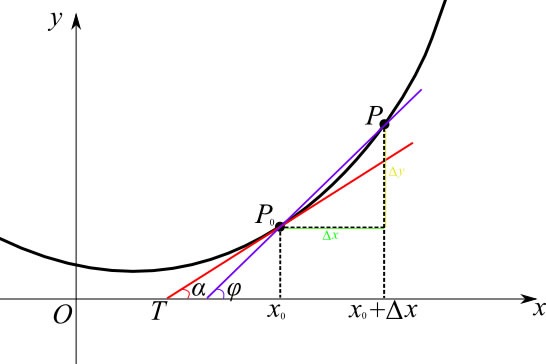
导数
定义:
设 在
的某个邻域
内有定义,并设
。
如果:
存在,
则称:
在
处可导,并称上述极限为
在
处的导数
记为:
若记,则在
点的导数又可记成
等等。
如果在区间
内每一点都可导,则称
在
内可导,
称为
在
内的导函数,简称导数。
在定义式中,若记,则该式可改写为
注:
导数的定义式中,必须要有,并且其中的
是
附近的
处的函数值,没有这些,就谈不上求导数,在按定义求导数时,必须注意。
举例说明
平均速度 ,速度的概念是一个瞬时概念,但如何表示瞬时速度?
瞬时经过的路程,那么这一小段的平均速度就是
当 时也就是瞬时的速度了:








 本文介绍了导数的基本概念,包括导数的定义、记法以及可导性的条件。通过举例说明,解释了如何从平均速度过渡到瞬时速度,从而理解导数在表示瞬时变化率中的作用。
本文介绍了导数的基本概念,包括导数的定义、记法以及可导性的条件。通过举例说明,解释了如何从平均速度过渡到瞬时速度,从而理解导数在表示瞬时变化率中的作用。
















 416
416

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








