说到一致(Consistency),其实很多代价都有这个内涵,如 MSE 代价,最小化预测与标签的差值,也就是希望预测与标签能够一致。其他的代价,如 KL 散度、交叉熵代价也类似。所以一致性,是一种非常内在而本质的目标,可以让深度网络进行有效学习。
但是在半监督中,无标签数据并没有标签,因而勤劳而美丽的科研工作者们就想出了各种无需标签信息的 Consistency Regularization,随着 Consistency Regularizaton 的不断发展,一度成为半监督深度学习发展史上耀眼的 SOTA。
**Consistency Regularization 的主要思想是:对于一个输入,即使受到微小干扰,其预测都应该是一致的。 **
例如,某人的裸照(干净的输入)和其有穿衣服的照片(受到干扰的照片),你也应该能知道这是同一个人(一致性)。 当然,这个干扰不能太大(例如衣服把整个人都遮住了)。
Consistency Regularization 虽然做法简单,但是却具有很多良好的作用,将会在下面的文章中阐述。

这是 NIPS 2014 年发表的工作,其提出了一个概念:pseudo-ensemble,一个 pseudo-ensemble 是一系列子模型(child model),这些子模型通过某种噪声过程(noise process)扰动父模型(parent model)得到。
Pseudo-ensemble 与其他的有关扰动的方法的区别在于:其他的方法只考虑在输入空间的扰动,而 pseudo-ensemble 还考虑在模型空间(model space)上的扰动。
一个典型的 pseudo-ensemble 就是 Dropout。 但是,除了 dropout 以外,我没怎么想到其他的模型空间上的扰动,看论文的公式貌似是在网络的中间表示添加噪声?论文有代码,但我没怎么看,有不同意见的同学可以评论里提出。
其有监督代价函数如下:
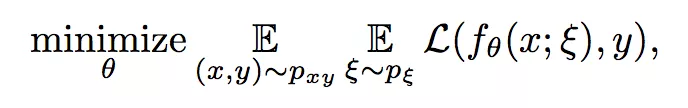
其中 θ 是网络参数,ξ 表示某种噪声过程,该有监督代价函数就是让扰动得到的子模型与标签 y 一致。
论文中还提出其半监督形式:The Pseudo-Ensemble Agreement regularizer (PEA),其形式如下:
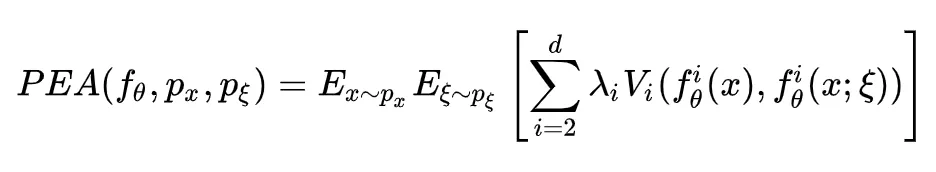
其中 d 是网络的层数,其含义应该是把父模型的每一层中间表示,与子模型的进行一致正则, V 是某种惩罚函数,如 MSE 代价(注:最后一层的中间表示即网络的预测)。
现在回顾一下 Consistency regularization 的思想:对于一个输入,受扰微小扰动后,其预测应该是一致的。
PEA 的含义我认为就是,对于一个输入,受到扰动后,其所有的中间表示,都应该一致。其实根据后面更多的论文,这个约束可能强力些。
PEA 的目的是,使得模型对扰动具有鲁棒性,因为鲁棒的模型泛化性能更好,同时还能学习数据的内在不变性(作用 1)。

这是 NIPS 2016 年发表的工作。随机性在大部分的学习系统中起到重要的作用,深度学习系统也如此。一些随机技术,如随机数据增强、Dropout、随机最大池化等,可以使得使用 SGD 训练的分类器具有更好的泛化性和鲁棒性。
而且这种不确定性的存在,使得模型对同一个样本的多次预测结果可能不同。因此论文提出一个无监督代价(即我说的半监督正则),其通过最小化对同一个样本的多次预测,利用这种随机性来达到更好的泛化性能。该无监督代价形式如下:
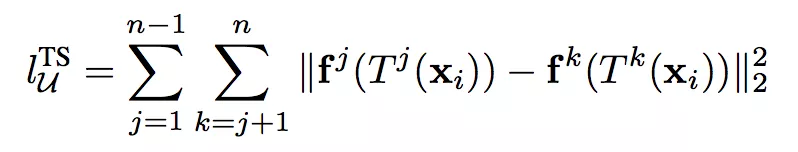
其中
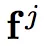
代表对输入
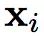
的第 j 次预测, T 表示某种数据变换。除了对样本做变换,在网络内也使用类似 Dropout 或随机池化等技术产生随机性。
虽然感觉很类似,但是这两篇论文很值得一读啊,论文里提出许多的观点和想法,一直延续至今,信息量挺大。

这篇在 ICLR 2017 年的工作提出了一个我称之为 peer-consistency 的正则项,即 π 模型,也是我最开始对 Consistency Regularization 的认知的由来。
π 模型认为,同一个输入,在不同的正则和数据增强条件下,网络对其预测应该是一致的。其无监督代价部分如下:
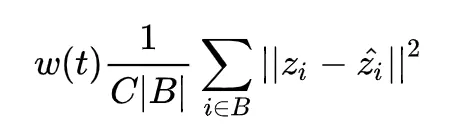
其中 zi 是网络的一个预测,而
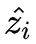
是网络对同一个样本在不同的正则和数据增强条件下的一个预测,然后让着两个预测一致。看起来很像前面两篇文章的简化版,但是效果好啊,这也是我说前面的约束太强的原因。
w(t) 是权重函数,是迭代次数的函数。由于在网络的初始阶段,网络的预测十分不准(尤其是半监督中有标签数据有限的情况),这时的网络预测靠不住的,因此这无监督代价在初始时的权重应该设置得比较小,到后期再慢慢增大。
w(t) 非常关键,论文中使用了一个高斯爬升函数,具体可以看论文。我的理解是,这种 peer-consistency 鼓励一个样本点的扰动不变性,其实鼓励了预测函数(即网络)对样本的邻域具有光滑性(作用 2)。
而且把 peer-consistency 看做是一种标签正则,可以从最大熵模型来理解 peer-consistency,具体可参考 Regularizing Neural Networks by Penalizing Confident Output Distributions,_** **_ICLR 17。
论文中还提出了另一种更强大的方法,但由于不在该主题下,不讲,可能会另开一篇文章讲吧,同学可以自己看论文。

这篇 NIPS 2017 的工作提出了一个 peer-consistency 的升级版,Teacher-student Consistency。 其除了 consistency 这个思想外,还有“模型成功的关键在于 target 的质量”这个动机。
具体想法就是,我从当前的模型(Student model),构造出一个比 Student model 更好一些的 Teather model,然后用这个 Teacher model 的预测来训练 Student model(即 Consistency Regularization)。 其无监督代价部分如下:
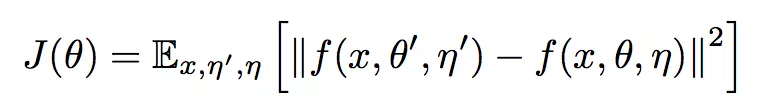
其中 f(x, θ', η') 是 Teacher model 的预测, f(x, θ, η) 是 Student model 的预测。但问题是,怎么去构造这个更好一些的 Teacher model?
论文提出的方法是,对 Student model 每次更新的模型做移动平均,移动平均后的模型就是 Teacher model,Teacher model 也不用反向传播更新,就参数的移动平均足以。其移动平均公式如下:
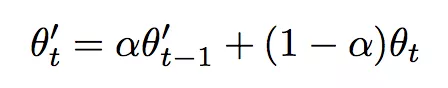
有没有一种好神奇的感觉,效果还非常地好。论文还用实验说明,其能形成一个良好的循环,得到一个 Student model,构造一个更好的 Teacher model,然后这个 Teacher model 又能用来升级 Student model,然后又……
当然,由于 Student model 刚开始只用有限的有标签数据训练,其性能并不好,因此该无监督代价同样需要乘一个权重(函数),这个权重函数和 Temporal Ensembling for Semi-supervised Learning 一样。

这是 CVPR 2018 的工作,该工作指出,前面的 consistency 都是只作用在单个数据点上,即都是对同一个数据点的增强。因此,**论文提出一种 features consistency,其认为属于同一个类别的数据特征(分类层前面的中间表示)应该具有一致性。 **
但是,无监督数据并没有标签,我怎么知道是不是属于同一类,论文使用前面的半监督方法的预测作为样本的标签,即 pseudo label,来构造这种属于同一类别的特征一致性。
虽然感觉这是取了巧,但是实验效果还不错,而且想法也很对,还是分享一下。其特征一致性的正则如下:
![]()
其中,若预测的为属于同一类,则 Wij=1,不属于同一类则为 0。 h(xi) 表示样本的(深度)特征。
当然,这个代价函数本身是 1994 年 NIPS 一个工作提出来的,被这篇论文重新活用了,还是那句话,想法对,效果也好。
还有一篇 Consistency Regularization 的算是 Virtual Adversarial Training: a Regularization Method for Supervised and Semi-supervised Learning,虽然论文讲的是如何计算对抗噪声,但我看了代码觉得其实和 consistency 很像,只不过是普通扰动变成了对抗扰动。
另一篇类似 CVPR 2018 SNTG 的论文是 ECCV 2018 的 Transductive Semi-Supervised Deep Learning using Min-Max Features,不过大部分概念我说过了,论文自己去看就行,思想差不多。
QQ:战、血舞皇朝、2125364717























 948
948

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










