NLP学习笔记(三)

• 三、归并排序

1、基本思想

  归并排序（MERGE-SORT）是利用归并的思想实现的排序方法，该算法采用经典的分治（divide-and-conquer）策略（分治法将问题分(divide)成一些小的问题然后递归求解，而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起，即分而治之)。

可以看到这种结构很像一棵完全二叉树，本文的归并排序我们采用递归去实现（也可采用迭代的方式去实现）。分阶段可以理解为就是递归拆分子序列的过程，递归深度为log2n。

合并相邻有序子序列
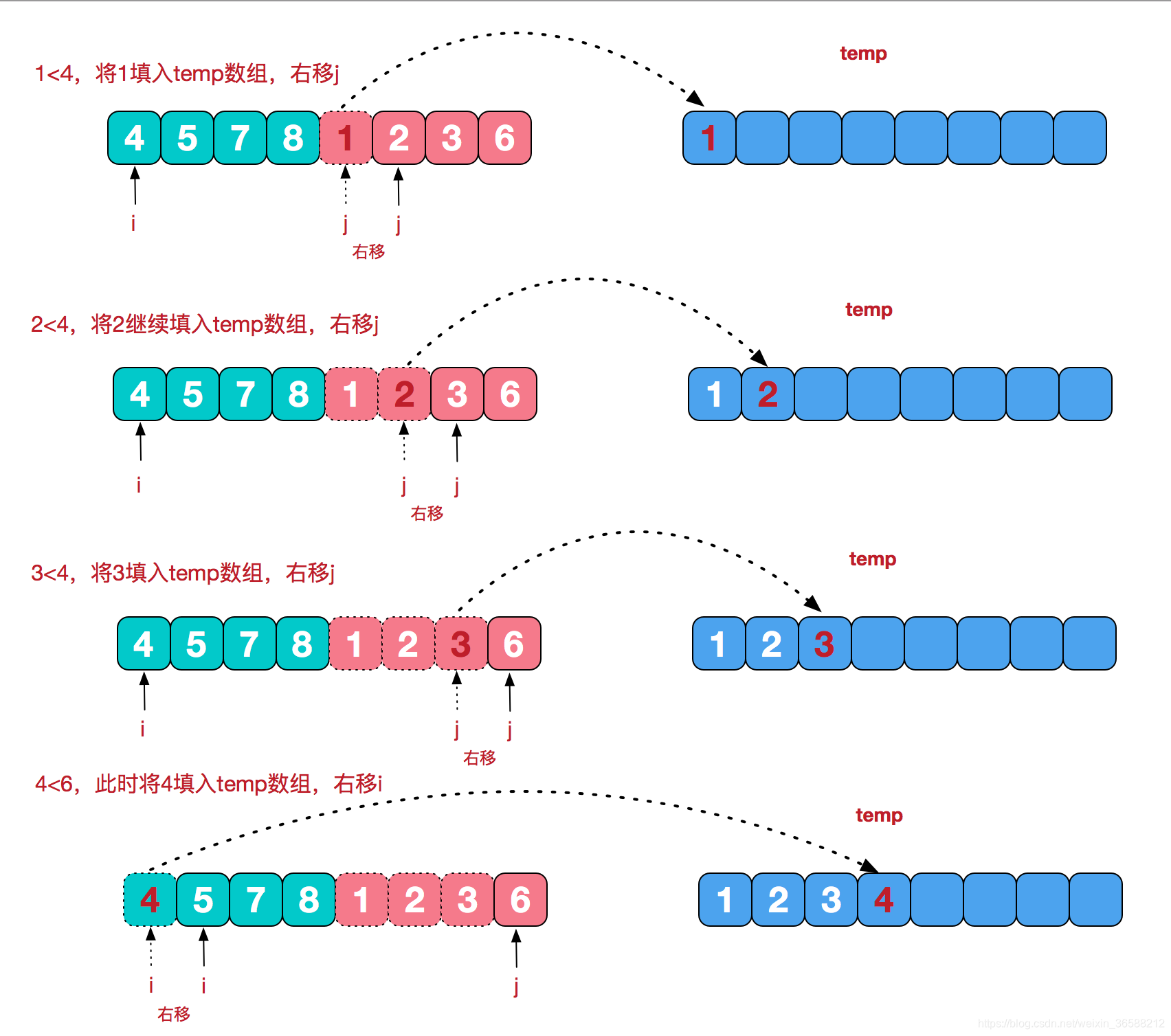
　　再来看看治阶段，我们需要将两个已经有序的子序列合并成一个有序序列，比如上图中的最后一次合并，要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列，合并为最终序列[1,2,3,4,5,6,7,8]，来看下实现步骤。

归并排序时间复杂度可以这样得到

归并排序时间复杂度   T(n) = aT(n/b)+f(n)

则有如下结果：

时间复杂度T(n)为：

k可以通过f(n)得出：

假设f(n)=n²，可以看做

所以k=0.

 

所以针对上述归并算法的算法复杂度为：

参考：https://www.cnblogs.com/chengxiao/p/6194356.html

 

• 四、斐波那契数
   

1、定义

    斐波那契数，亦称之为斐波那契数列（意大利语： Successione di Fibonacci)，又称黄金分割数列、费波那西数列、费波拿契数、费氏数列，指的是这样一个数列：1、1、2、3、5、8、13、21、……在数学上，斐波那契数列以如下被以递归的方法定义：F0=0，F1=1，Fn=Fn-1+Fn-2（n>=2，n∈N*），用文字来说，就是斐波那契数列由 0 和 1 开始，之后的斐波那契数列系数就由之前的两数相加。

2、递归求斐波那契数时间复杂度

求法：通过二叉树求时间复杂度

由此得出T(n)=O(2^(n-1))≈O(2^n)

复杂度这么高的原因就是，递归里很多数是重复求取的，例如f(3),在求f(4)和f(5)中都求解了,以此类推

3、递归求斐波那契数空间复杂度

因为使用递归方式，所以采用了压栈方式，占用空间就是栈占用空间，又因为f(1)入栈已经是递归的最后一层，所以入栈后又出栈，不占用空间，所以空间复杂度为O(n)

4、代码

#递归方式
def fib2(n):
    #base case
    if n<3:
        return 1
    return fib(n-1)+fib(n-2)

print(fib2(50))

优化一下，使用数组方式：

import time
import numpy as np
#数组方式
def fib(n):
    number=np.zeros(n)
    number[0]=1
    number[1]=1
    for i in range(2,n):
        number[i]=number[i-1]+number[i-2]
    return number[n-1]
print(fib(50))

又因为我们并不需要前面的数，只需要最后个数，再进行优化可得

def fib(n):
    a=1
    b=1
    c=0
    for i in range(2,n):
        c=a+b
        a=b
        b=c
    return c