numpy6随机模块和其他

随机模块random

二项分布

二项分布：np.random.binomial(n, p, size)
产生size个随机数，每个随机数来自n次尝试中的成功次数，其中每次尝试成功的概率为p。
返回值：长度size的数组，每一项为每次的成功次数
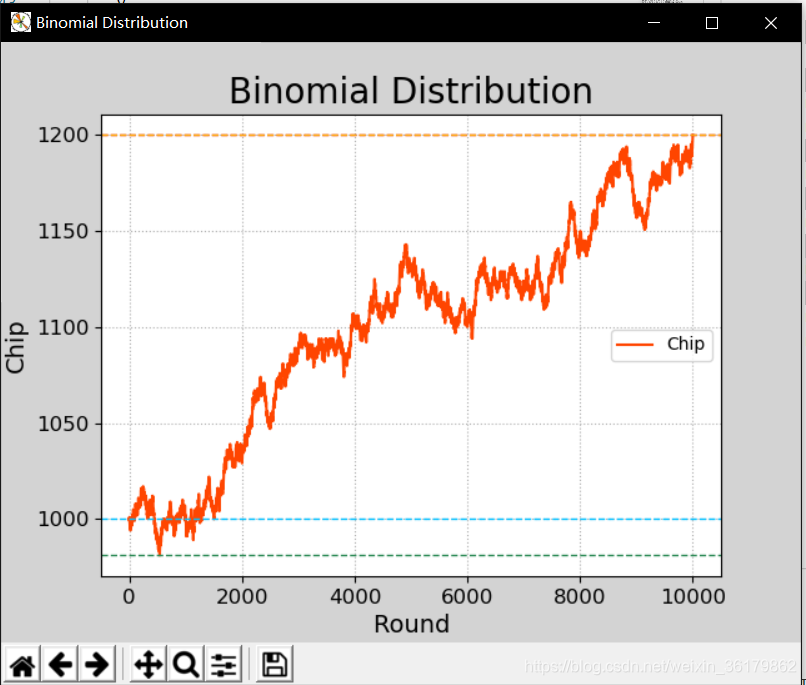
猜硬币游戏：初始筹码1000，每轮猜9次，猜对5次及5次以上为赢，筹码加1，否则为输，筹码减1，求10000轮的过程中手中筹码的变化。
1 2 3 4 5 6
5 1 2 0 0 2
0 2 0 6 1 1
…

# -*- coding: utf-8 -*-
from __future__ import unicode_literals
import numpy as np
import matplotlib.pyplot as mp
outcomes = np.random.binomial(9, 0.5, 10000)
chips = [1000]
for outcome in outcomes:
    if outcome >= 5:
        chips.append(chips[-1] + 1)
    else:
        chips.append(chips[-1] - 1)
chips = np.array(chips)
mp.figure('Binomial Distribution',
          facecolor='lightgray')
mp.title('Binomial Distribution', fontsize=20)
mp.xlabel('Round', fontsize=14)
mp.ylabel('Chip', fontsize=14)
mp.tick_params(labelsize=12)
mp.grid(linestyle=':')
o, h, l, c = 0, chips.argmax(), chips.argmin(), \
    chips.size - 1
if chips[o] < chips[c]:
    color = 'orangered'
elif chips[c] < chips[o]:
    color = 'limegreen'
else:
    color = 'dodgerblue'
mp.plot(chips, c=color, label='Chip')
mp.axhline(y=chips[o], linestyle='--',
           color='deepskyblue', linewidth=1)
mp.axhline(y=chips[h], linestyle='--',
           color='crimson', linewidth=1)
mp.axhline(y=chips[l], linestyle='--',
           color='seagreen', linewidth=1)
mp.axhline(y=chips[c], linestyle='--',
           color='orange', linewidth=1)
mp.legend()
mp.show()

真希望我的股票也这样。。。

超几何分布

超几何分布：np.random.hypergeometric(ngood, nbad, nsample, size)
产生size个随机数，每个随机数来自随机抽取nsample个样本中
好样本的个数，总样本由ngood个好样本和nbad个坏样本组成
返回值：抽到的好样本的个数。
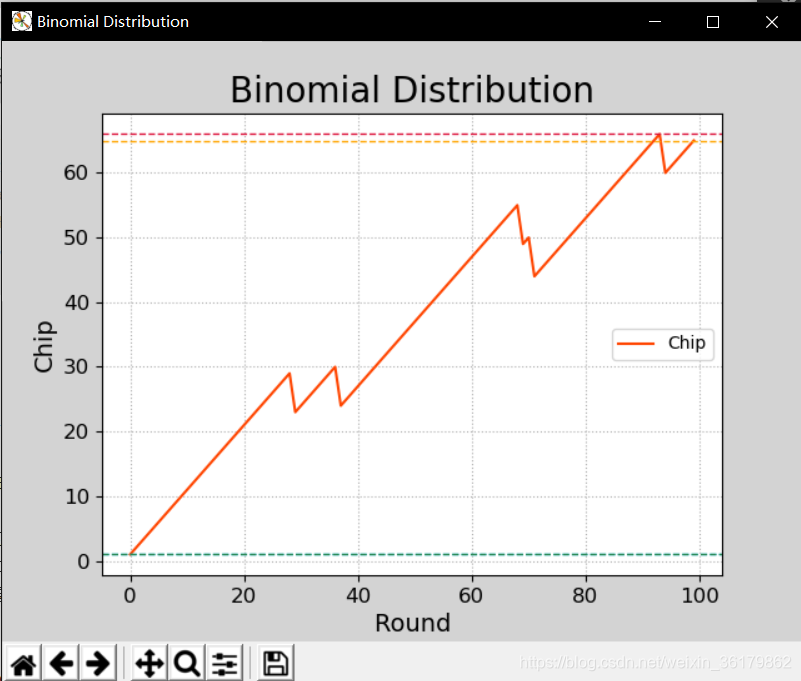
模球游戏：将25个好球和1个坏球放在一起，每次模3个球，全为好球加1分，只要摸到了坏球减6分，求100轮的过程中分值的变化。

import numpy as np
import matplotlib.pyplot as mp
outcomes=np.random.hypergeometric(25,1,3,100)
print(outcomes)
value=0
outcomes[outcomes==3]=1
outcomes[outcomes==2]=-6
print(outcomes)
for i in range(len(outcomes)):
    value+=int(outcomes[i])
    outcomes[i]=value
mp.figure('Binomial Distribution',
          facecolor='lightgray')
mp.title('Binomial Distribution', fontsize=20)
mp.xlabel('Round', fontsize=14)
mp.ylabel('Chip', fontsize=14)
mp.tick_params(labelsize=12)
mp.grid(linestyle=':')
o, h, l, c = 0, outcomes.argmax(), outcomes.argmin(), \
    outcomes.size - 1
if outcomes[o] < outcomes[c]:
    color = 'orangered'
elif outcomes[c] < outcomes[o]:
    color = 'limegreen'
else:
    color = 'dodgerblue'
mp.plot(outcomes, c=color, label='Chip')
mp.axhline(y=outcomes[o], linestyle='--',
           color='deepskyblue', linewidth=1)
mp.axhline(y=outcomes[h], linestyle='--',
           color='crimson', linewidth=1)
mp.axhline(y=outcomes[l], linestyle='--',
           color='seagreen', linewidth=1)
mp.axhline(y=outcomes[c], linestyle='--',
           color='orange', linewidth=1)
mp.legend()
mp.show()

想说的话同上：

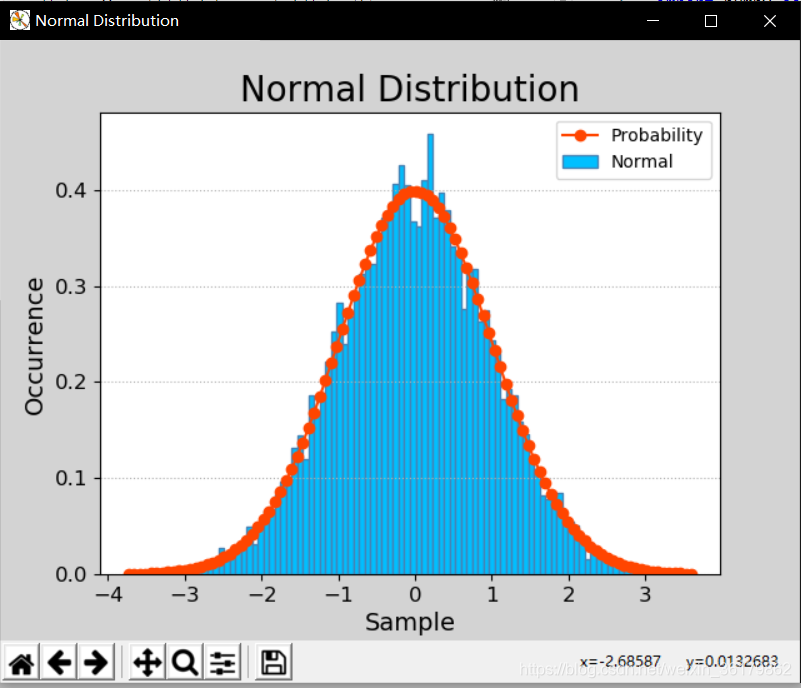
标准正态分布

正态分布：np.random.normal(平均值，标准差，size=样本数)
标准正态分布：np.random.normal(size=样本数)
产生size个随机数，服从标准正态(平均值=0, 标准差=1)分布。

# -*- coding: utf-8 -*-
from __future__ import unicode_literals
import numpy as np
import matplotlib.pyplot as mp
samples = np.random.normal(size=10000)
mp.figure('Normal Distribution',
          facecolor='lightgray')
mp.title('Normal Distribution', fontsize=20)
mp.xlabel('Sample', fontsize=14)
mp.ylabel('Occurrence', fontsize=14)
mp.tick_params(labelsize=12)
mp.grid(axis='y', linestyle=':')
bins = mp.hist(samples, 100, normed=True,
               edgecolor='steelblue',
               facecolor='deepskyblue',
               label='Normal')[1]
probs = np.exp(-bins ** 2 / 2) / np.sqrt(2 * np.pi)
mp.plot(bins, probs, 'o-', c='orangered',
        label='Probability')
mp.legend()
mp.show()

都是腰间盘，你咋这么突出

排序

间接关联排序
间接排序：以样本下标而非样本本身来表示排序的结果。
0 1 2 3 4
原始样本：[10 40 30 50 20]
直接排序：[10 20 30 40 50]
间接排序：[ 0 4 2 1 3 ]
关联排序：对被排序序列中值相同的元素，参考另一个序列的升序条件决定其顺序。
0 1 2 3 4
待排序列：[10 40 30 40 20]
参考序列：[ B C A E C ]
排序序列：[ 0 4 2 1 3 ]
np.lexsort((参考序列, 待排序列))->有序下标
np.sort_complex(复数数组)->直接排序结果
按照实部的升序排列，若实部相同，参考虚部的升序
[1 2 4 5 6 8 9]<-[7 3]
np.searchsorted([1 2 4 5 6 8 9], [7 3])->插入位置
被插序列 插入序列
np.insert(被插序列, 插入位置, 插入序列)->插入结果

# -*- coding: utf-8 -*-
from __future__ import unicode_literals
import numpy as np
names = np.array(['zhangfei', 'zhaoyun', 'guanyu',
                  'huangzhong', 'machao'])
scores = np.array([90, 70, 60, 70, 90])
ages = np.array([50, 30, 20, 20, 40])
# 按照成績的升序打印姓名，成績相同的參考年齡的升序
print(names[np.lexsort((ages, scores))])
complexes = scores + ages * 1j
sorted_complexes = np.sort_complex(complexes)
print(complexes, sorted_complexes, sep='\n')
#             0  1 *2  3  4 *5  6
a = np.array([1, 2, 4, 5, 6, 8, 9])
print(a)
b = np.array([7, 3])
print(b)
c = np.searchsorted(a, b)
print(c)
# 将b数组中的元素按照c数组中的对应
# 位置插入a数组中，返回插入结果
d = np.insert(a, c, b)
print(d)

间接关联排序

联合间接排序：numpy.lexsort((参考序列, 待排序列))
                                                ->有序索引
[张三 李四 王五 赵六]
[70 60 80 70]<-[30 20 30 20]

复数排序

numpy.sort_complex(复数数组)
按照实部的升序排列，对于实部相同的元素，参考虚部的升序，直接返回排序后的结果数组。
numpy.searchsorted(有序序列, 待插序列)
numpy.insert(被插序列, 位置序列, 待插序列)
->位置数组，表示将待插序列中的元素插入到有序序列中的哪些位置处，结果依然有序
->将待插序列中的元素，按照位置序列中的位置，插入到被插序列中，返回插入后的结果

# -*- coding: utf-8 -*-
from __future__ import unicode_literals
import numpy as np
ages = np.array([30, 20, 30, 20])
scores = np.array([70, 60, 80, 70])
names = np.array(['zhangsan', 'lisi',
                  'wangwu', 'zhaoliu'])
# 按照成绩的升序打印姓名，成绩相同的按照年龄的升序排列
print(np.take(names, np.lexsort((ages, scores))))
compleies = scores + ages * 1j
print(compleies)
sorted_compleies = np.sort_complex(compleies)
print(sorted_compleies)
#             0  1  2  3  4  5  6
a = np.array([1, 2, 4, 5, 6, 8, 9])
b = np.array([7, 3])
c = np.searchsorted(a, b)
print(c)
d = np.insert(a, c, b)
print(d)

插值

import scipy.interpolate as si
si.interp1d(离散水平坐标, 离散垂直坐标,
kind=插值算法(缺省为线性插值))->插值器
插值器(水平坐标)->垂直坐标

# -*- coding: utf-8 -*-
from __future__ import unicode_literals
import numpy as np
import scipy.interpolate as si
import matplotlib.pyplot as mp
min_x, max_x = -2.5, 2.5
con_x = np.linspace(min_x, max_x, 1001)
con_y = np.sinc(con_x)
dis_x = np.linspace(min_x, max_x, 11)
dis_y = np.sinc(dis_x)
# 线性插值
linear = si.interp1d(dis_x, dis_y)
lin_x = np.linspace(min_x, max_x, 51)
lin_y = linear(lin_x)
# 三次样条插值
cubic = si.interp1d(dis_x, dis_y, kind='cubic')
cub_x = np.linspace(min_x, max_x, 51)
cub_y = cubic(cub_x)
mp.figure('Interpolation', facecolor='lightgray')
mp.subplot(221)
mp.title('Continuous', fontsize=16)
mp.ylabel('y', fontsize=12)
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
mp.plot(con_x, con_y, c='hotpink',
        label='Continuous')
mp.legend()
mp.subplot(222)
mp.title('Discrete', fontsize=16)
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
mp.scatter(dis_x, dis_y, c='orangered', s=80,
           label='Discrete')
mp.legend()
mp.subplot(223)
mp.title('Linear', fontsize=16)
mp.xlabel('x', fontsize=12)
mp.ylabel('y', fontsize=12)
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
mp.plot(lin_x, lin_y, 'o-', c='limegreen',
        label='Linear')
mp.scatter(dis_x, dis_y, c='orangered', s=80,
           zorder=3)
mp.legend()
mp.subplot(224)
mp.title('Cubic', fontsize=16)
mp.xlabel('x', fontsize=12)
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
mp.plot(cub_x, cub_y, 'o-', c='dodgerblue',
        label='Cubic')
mp.scatter(dis_x, dis_y, c='orangered', s=80,
           zorder=3)
mp.legend()
mp.tight_layout()
mp.show()

积分

积分计算：
import scipy.integrate as si
si.quad(积分函数, 积分下限, 积分上限)
->积分函数在[积分下限,积分上限]区间的定积分
注意：这里的积分函数很有趣，使用的直接就是python的函数格式，举个例子：
def f(x):
return 2 * x ** 2 + 3 * x + 4
函数的格式是这样的。另外这个函数还有个奇葩的地方，我之前一直在想为什么代码里面没有进行标量函数矢量化（捂脸哭），后来我才发现，tm里面涉及的方法所使用的乘法，加法等都是参数x重写了的。
从这里也可以看出来，这里的积分得到的是近似值，不是数学上的完全解。
示例：

# -*- coding: utf-8 -*-
from __future__ import unicode_literals
import numpy as np
import scipy.integrate as si
import matplotlib.pyplot as mp
import matplotlib.patches as mc

def f(x):
    y = 2 * x ** 2 + 3 * x + 4
    return y

a, b = -5, 5
x1 = np.linspace(a, b, 1001)
y1 = f(x1)
n = 50
x2 = np.linspace(a, b, n + 1)
y2 = f(x2)
area = 0
for i in range(n):
    area += (y2[i] + y2[i + 1]) * (
        x2[i + 1] - x2[i]) / 2
print(area)
area = si.quad(f, a, b)[0]
print(area)
mp.figure('Area', facecolor='lightgray')
mp.title('Area', fontsize=20)
mp.xlabel('x', fontsize=14)
mp.ylabel('y', fontsize=14)
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
mp.plot(x1, y1, c='orangered', linewidth=6,
        label=r'$y=2x^2+3x+4$', zorder=0)
for i in range(n):
    mp.gca().add_patch(mc.Polygon(
        [[x2[i], 0], [x2[i], y2[i]],
         [x2[i + 1], y2[i + 1]], [x2[i + 1], 0]],
        fc='deepskyblue', ec='dodgerblue',
        alpha=0.5))
mp.legend()
mp.show()

无效值nan分析

import numpy as np
a = np.array([10, np.nan, 30, np.nan, 50])
print(a.shape, a.size, a.dtype, type(a[1]), a[1])
# np.nan这个值很有趣，他不大于1000，不小于1000，只是不等于1000，\
# 该值可以使无穷大也可以是无穷下，具体是多少需要通过调用的函数定义。
print(np.nan > 1000)
print(np.nan < 1000)
print(np.nan == 1000)
print(np.nan != 1000)
print(np.nan + 1000, np.nan - 1000)
# nan元素既是极大值也是极小值
print(np.max(a), np.min(a))
#返回的是nan的物理地址，无力吐槽这一点。。。。。。。。。。。
print(np.argmax(a), np.argmin(a))
# 忽略nan元素，获取极大/极小值
print(np.nanmax(a), np.nanmin(a))
# 获取最大值最小值的下标
print(np.nanargmax(a), np.nanargmin(a))
print(np.msort(a))

利率计算

import numpy as np
# 终值 = fv(利率, 期数, 每期支付, 现值)
# 将1000元以1%的年利率存入银行5年，每年加存100元，
# 到期后本息合计多少钱？
fv = np.fv(0.01, 5, -100, -1000)
print(round(fv, 2))
# 现值 = pv(利率, 期数, 每期支付, 终值)
# 将多少钱以1%的年利率存入银行5年，每年加存100元，
# 到期后本息合计1561.11？
pv = np.pv(0.01, 5, -100, 1561.11)
print(round(pv, 2))
# 净现值 = npv(利率, 现金流)
# 将1000元以1%的年利率存入银行5年，每年加存100元，
# 相当于一次性存入多少钱？
npv = np.npv(0.01, [-1000, -100, -100,
                    -100, -100, -100])
print(round(npv, 2))
fv = np.fv(0.01, 5, 0, -1485.34)
print(round(fv, 2))
# 内部收益率 = irr(现金流)
# 将1000元存入银行5年，以后逐年提取100元、200元、
# 300元、400元、500元，银行利率达到多少，可在最后一
# 次体现后偿清全部本息，即净现值为0？
irr = np.irr([-1000, 100, 200, 300, 400, 500])
print(round(irr, 2))
npv = np.npv(irr, [-1000, 100, 200, 300, 400, 500])
print(round(npv, 2))
# 每期支付 = pmt(利率, 期数, 现值)
# 以1%的年利率从银行贷款1000元，分5年还清，
# 每年还多少钱？
pmt = np.pmt(0.01, 5, 1000)
print(round(pmt, 2))
# 期数 = nper(利率, 每期支付, 现值)
# 以1%的年利率从银行贷款1000元，平均每年还款206.04元，
# 多少年还清全部本息？
nper = np.nper(0.01, -206.04, 1000)
print(np.round(nper))
# 利率 = rate(期数, 每期支付, 现值, 终值)
# 从银行贷款1000元，平均每年还款206.04元，
# 5年还清全部本息，年利率多少？
rate = np.rate(5, -206.04, 1000, 0)
print(round(rate, 2))