本文深入探讨了强化学习中的马尔科夫决策过程（MDP）与马尔科夫过程的区别，强调了MDP在动作和奖励上的特性。文章通过实例详细解释了随机策略，包括贪婪策略、ε-greedy策略和高斯策略。此外，还介绍了基于模型的动态规划算法中的策略迭代和值迭代算法，以及蒙特卡罗方法和时间差分学习的异同。最后，讨论了值函数逼近在解决大规模或连续状态空间问题中的重要性，并提及了DQN等深度强化学习方法的应用。
1 绪论
2 马尔科夫决策过程
2.4 习题
1. Q:马尔科夫过程与马尔科夫决策过程的区别。
A: 马尔科夫过程的定义：马尔科夫过程是一个二元组(S,P),且满足：S是有限状态集合，P是状态转移概率。状态转移概率矩阵为：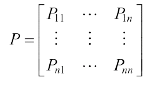
下面我们以一个例子来进行阐述。
如图2.2所示为一个学生的7种状态{娱乐，课程1，课程2，课程3，考过，睡觉，论文}，每种状态之间的转换概率如图所示。则该生从课程1开始一天可能的状态序列为:
课1-课2-课3-考过-睡觉
课1-课2-睡觉
以上状态序列称为马尔科夫链。当给定状态转移概率时，从某个状态出发存在多条马尔科夫链。对于游戏或者机器人，马尔科夫过程不足以描述其特点，因为不管是游戏还是机器人，他们都是通过动作与环境进行交互，并从环境中获得奖励，而马尔科夫过程中不存在动作和奖励。将动作（策略）和回报考虑在内的马尔科夫过程称为马尔科夫决策过程。
马尔科夫决策过程
马尔科夫决策过程是由元组(S,A,P,R,γ)描述，其中：
S为有限的状态集
A为有限的动作集
P为状态转移概率
R为回报函数
γ为折扣因子，用来计算累积回报。
注意，跟马尔科夫过程不同的是，马尔科夫决策过程的状态转移概率是包含动作的，即
举个例子如图2.3所示。
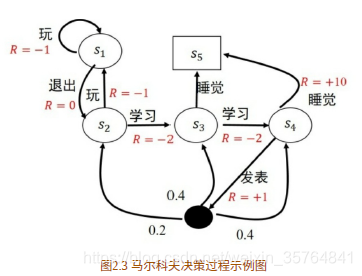
图2.3为马尔科夫决策过程的示例图，图2.3与图2.2对应。在图2.3中，学生有5个状态，状态集为S={s1,s2,s3,s4,s5},动作集为A={玩，退出，学习，发表，睡觉}，在图2.3中立即回报用R标记。
强化学习的目标是给定一个马尔科夫决策过程，寻找最优策略。所谓策略是指状态到动作的映射。
2. Q:随机策略的理解
A:在强化学习算法中，随机策略得到⼴泛应⽤，因为随机策略耦合了探索。后⾯要介绍的很多强化学习算
法的策略都采⽤随机策略，所以，很有必要理解什么是随机策略。随机策略常⽤符号π表⽰，它是指给定状态s时动作集上的⼀个分布。要理解分布⾸先要理解随机变量[2] 。
（1）随机变量。
随机变量是指可以随机地取不同值的变量，常⽤⼩写字⺟表⽰。在MDP中随机变量指的是当前的动作，⽤字⺟ 表⽰。在图2.3的例⼦中，随机变量 可取的值为“玩”、“退出”、“学习”、“发表”和“睡觉”。随机变量可以是离散的也可以是⾮离散的，在该例⼦中随机变量是离散的。有了随机变量，我们就可以描述概率分布了。
（2）概率分布。
概率分布⽤来描述随机变量在每个可能取到的值处的可能性⼤⼩。离散型随机变量的概率分布常⽤概率质量函数来描述，即随机变量在离散点处的概率。连续型随机变量的概率分布则⽤概率密度函数来描述。在图 2.3的例⼦中，指定⼀个策略π就是指定取每个动作的概率。
（3）条件概率。
策略π（a|s）是条件概率。条件概率是指在其他事件发⽣时，我们所关⼼的事件所发⽣的概率。在我们的例⼦中π（a|s）是指在当前状态s处，采取某个动作a的概率。当给定随机变量后
最低0.47元/天 解锁文章
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
