机器学习：支持向量机SVM简述

我的小程序：

待办计划：在不确定中前行

随笔日记：祭那些逝去的时光

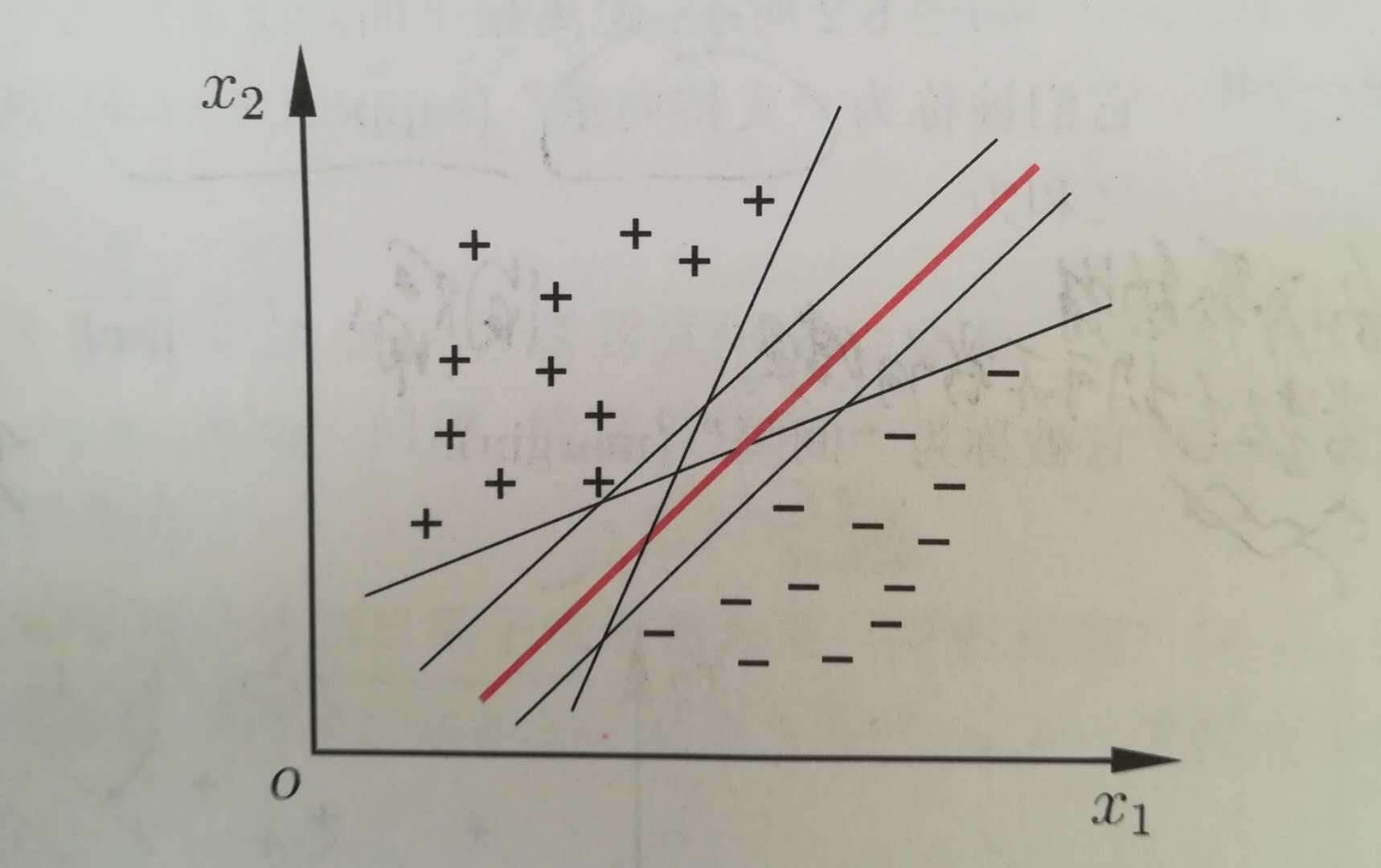
如上图所示，直观上看，红色那条线能更好的将样本分类，因为它更能容忍训练样本的扰动，对未见样本的泛化性能更强。支持向量机就是来寻找这样一个超平面（即上图中的红线），可用线性方程表示：w'x+b=0.其中w=(w1;w2;...;wd);如何找到这条红线？

样本空间任意一点x到超平面(w,b)的距离为：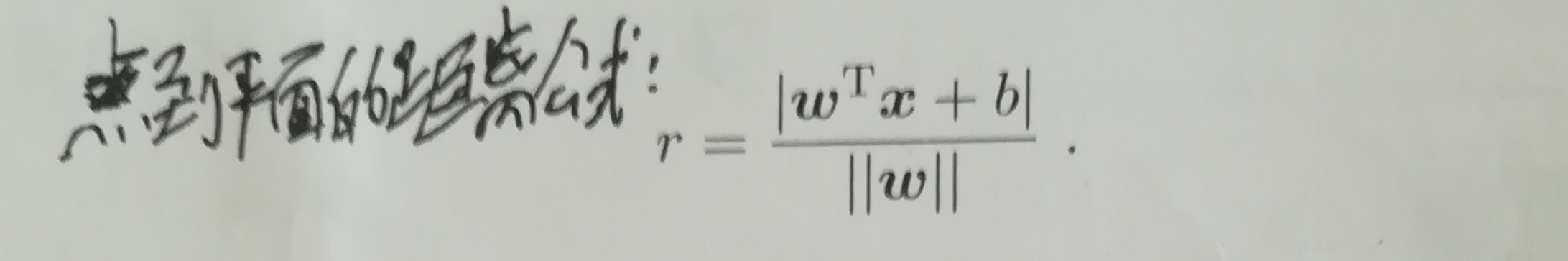

若超平面对样本正确分类，对于样本（Xi,Yi），若Yi=1（正例），则w'Xi+b>0；若Yi=-1(反例)，则w'Xi+b<0.可令：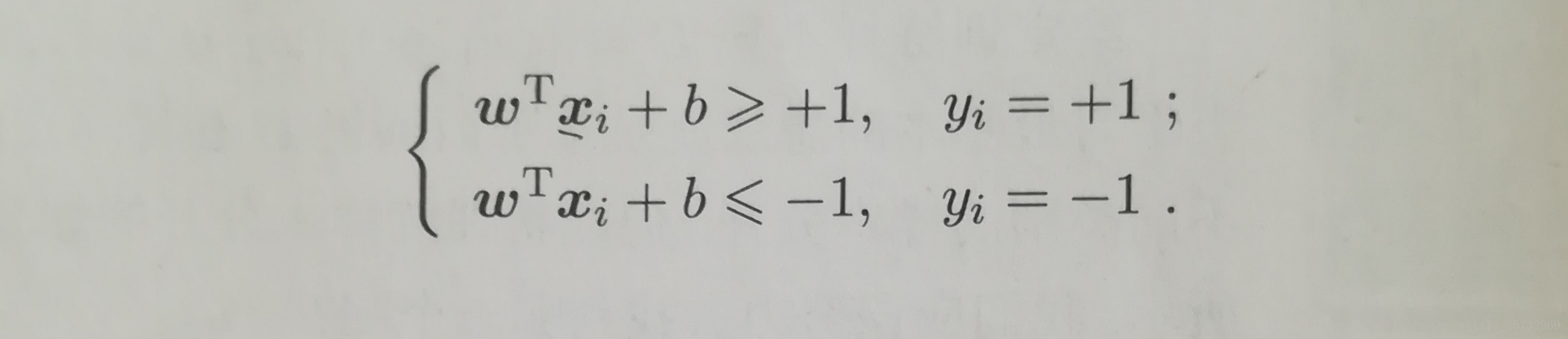

这里1，-1可以是任意常数c,-c，只是为了讨论方便取1，-1。

距离超平面最近的几个点使上面不等式成立，称这几个点为”支持向量“，两个异类支持向量到超平面的距离为：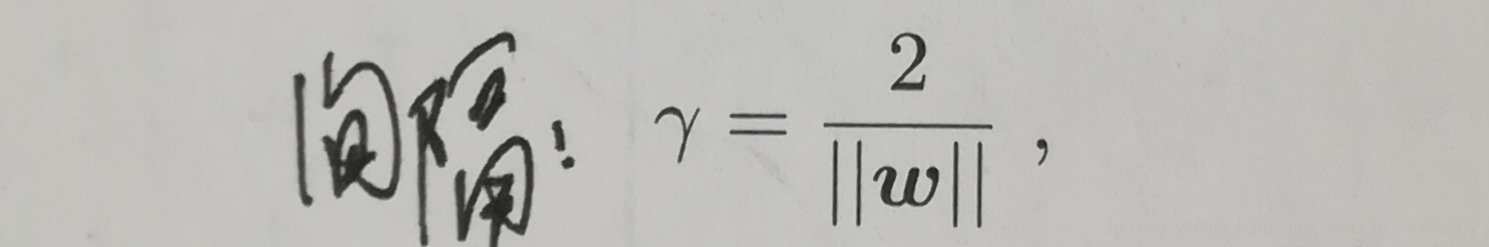

我们是要找到最大间隔的划分超平面，即找到一个超平面，它既能将样本正确划分，还满足离这个超平面最近的两个异类点到这个超平面的距离相等并且距离之和最大。回想我们最开始的那副图，为什么我们直观上觉得那条红线能更好的将样本分类，就是因为它就是满足这些要求的那个划分超平面。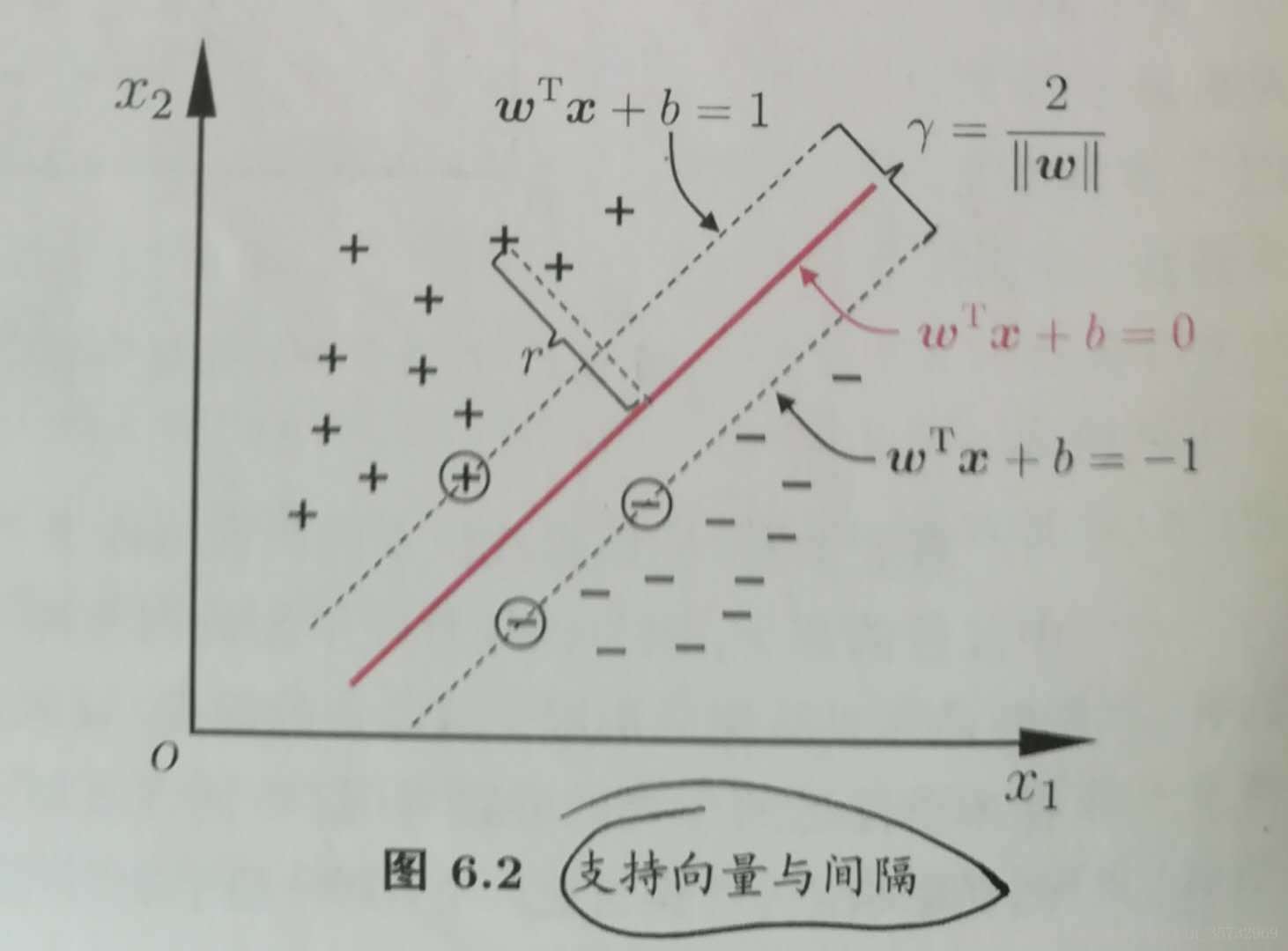

所以，我们要找的那个划分超平面就转化为如下的数学描述：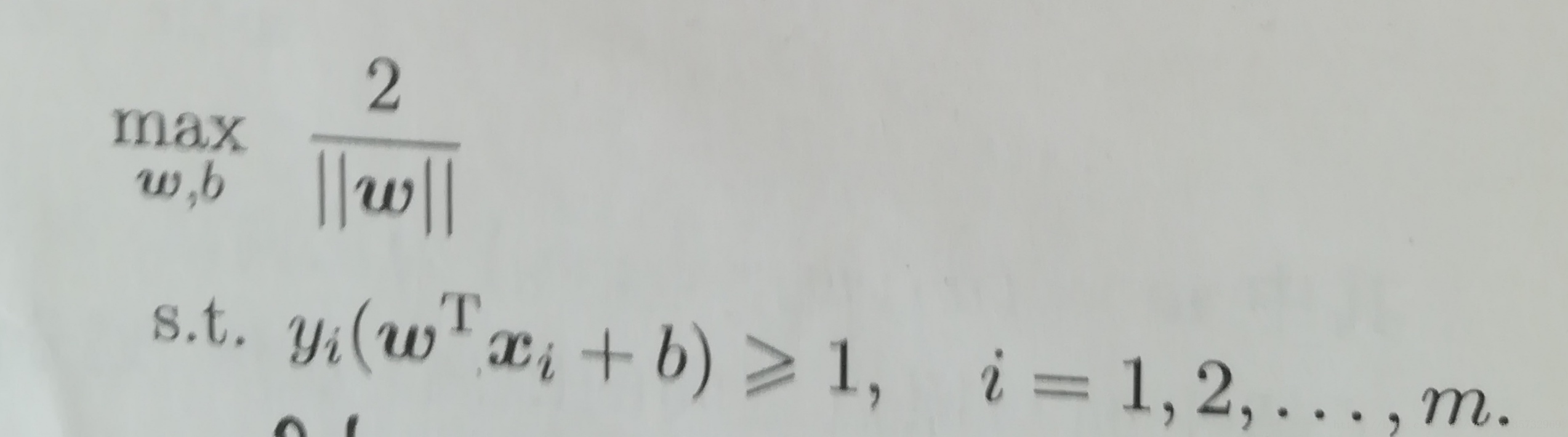

进一步转化，即：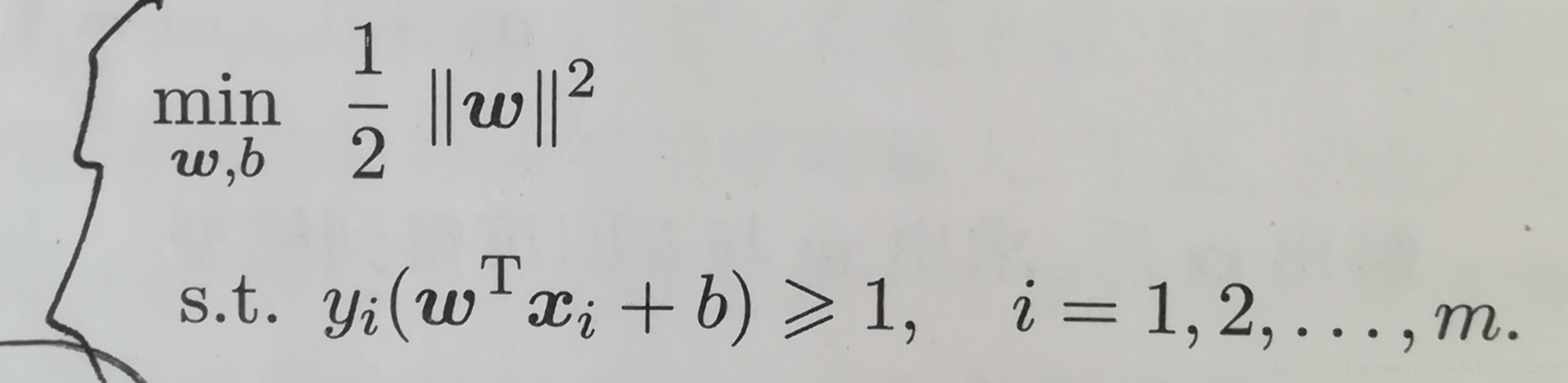

这就是支持向量机SVM的基本型。我们要做的就是求解参数w,b.这是一个凸二次规划问题，我们可以直接求解，但我们有更高效的方法：求它的对偶问题。见下篇。

待办计划：在不确定中前行

随笔日记：祭那些逝去的时光

参考资料：周志华《机器学习》

相关博文：

机器学习：支持向量机SVM对偶问题

拉格朗日乘子法原理：等式约束和不等式约束

机器学习：支持向量机SVM-软间隔