uniform分布_概率分布

正态分布

概率密度函数表示 -> 表示一个特定范围的值的发生概率

import numpy as np
import matplotlib.pyplot as plt
normal = np.random.normal(100, 6, 100)
plt.hist(normal, 10)
plt.show()

from scipy.stats import norm
x = np.arange(-3, 3, 0.001)
plt.plot(x, norm.pdf(x))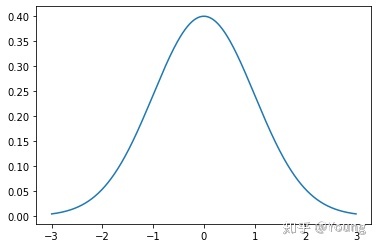

正态分布概率密度函数

均匀分布

均匀分布的概率分布函数是什么形状呢?在某这个范围之外，没有任何值，在这个范围之内，则是一条水平直线，因为所有值出现的概率都是相同的

uniform = np.random.uniform(-10, 10, 1000)
plt.hist(uniform, 50)
plt.show()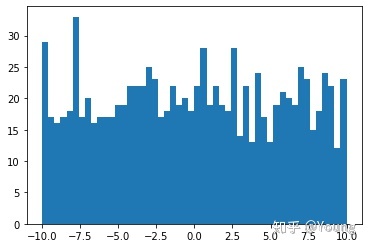

均匀分布图

指数概率分布与指数定律

指数概率分布函数，其函数值以指数方式下降。指数下降，是指一条曲线上在 0 附近的值发生的概率很高，但当远离 0 时，值会急速下降。

from scipy.stats import expon
x = np.arange(0, 10, 0.001) 
plt.plot(x, expon.pdf(x))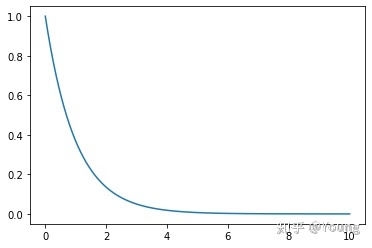

指数分布概率密度函数

二项式概率质量函数

概率质量函数处理的是离散数据

from scipy.stats import binom 
x = np.arange(0, 10, 0.001)
plt.plot(x, binom.pmf(x, 10, 0.5))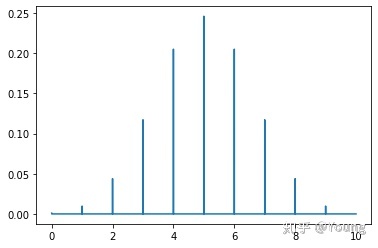

二项分布

泊松概率质量函数

如果你知道了在给定时间段内某个事情发生的平均次数，那么就可以使用泊松概率质量函数 来预测未来某个时段这个事情发生另一个次数的概率。

from scipy.stats import poisson
mu = 500
x = np.arange(400, 600, 0.5)
plt.plot(x, poisson.pmf(x, mu))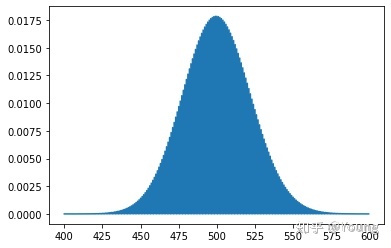

泊松分布

百分位数

一般来说，如果将数据集中所有数据排好顺序，那么第 x 个百分位数就是这样一个点:数据集中 x% 的数据都小于它。

矩

矩可以定义为描述概率密度函数形状的数量指标。

矩就是用在概率密度函数中描述数据分布形状的一个指标参数，它有一个非常棒的 数学定义:

一阶矩是均值，二阶矩是方差，三阶矩是偏度，四阶矩是峰度。我们已经 知道了什么是均值和方差。偏度表示数据的偏斜程度，即数据的尾部偏向哪一侧。峰度表示数据 分布有多尖锐，即从两侧向中间被挤压的程度。