拦截导弹
动态规划问题
某国为了防御敌国的导弹袭击,发展出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷:虽然它的第一发炮弹能够到达任意的高度,但是以后每一发炮弹都不能高于前一发的高度。某天,雷达捕捉到敌国的导弹来袭。由于该系统还在试用阶段,所以只有一套系统,因此有可能不能拦截所有的导弹。
输入导弹依次飞来的高度(雷达给出的高度数据是不大于30000
的正整数),计算这套系统最多能拦截多少导弹,并依次输出被拦截的导弹飞来时候的高度。
样例:
INPUT
389 207 155 300 299 170 158 65
OUTPUT
6(最多能拦截的导弹数)
389 300 299 170 158 65
1 // the solution of the missile 2 // use the DP(dynamic process) algorithms 3 #include<iostream> 4 5 #define MAX 100//define the missile max total number 6 using namespace std; 7 8 void calc(int a[],int i) 9 { 10 int b[MAX]; 11 b[0]=a[0]; 12 int ptr=0; 13 int m,k; 14 15 for( k=1;k<i;k++) 16 { 17 18 if(a[k]<=b[ptr])//加入数组末尾,非递减序列 19 { 20 ptr++; 21 b[ptr]=a[k]; 22 23 } 24 else//将a[k]放入数组B的正确位置 25 { 26 for(int n=0;n<=ptr;n++) 27 { 28 if(a[k]>b[n]) 29 { 30 b[n]=a[k]; 31 break; 32 } 33 } 34 35 } 36 37 38 } 39 cout<<"the total number of the missile is:"<<ptr+1<<endl; 40 for(k=0;k<=ptr;k++) 41 cout<<b[k]<<" "; 42 43 44 } 45 46 int main() 47 { 48 int arr[MAX]={0}; 49 int i; 50 cout<<"Input the total missile number:"; 51 cin>>i; 52 int k=0; 53 while(i>0) 54 { 55 cin>>arr[k]; 56 k++; 57 i--; 58 } 59 calc(arr,k); 60 return 0; 61 }
运行结果: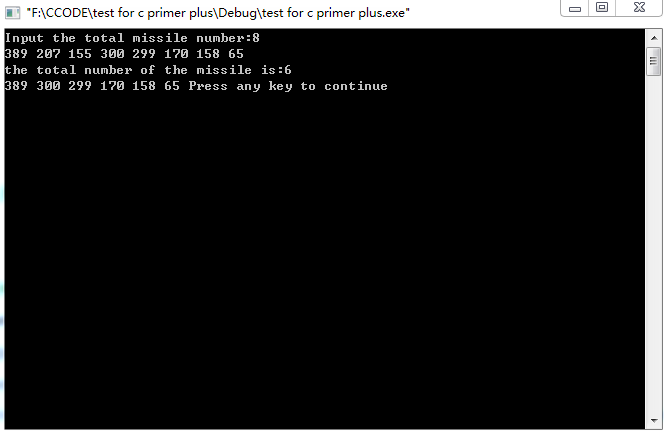




















 552
552

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








