3.3.1 最近对问题
问题描述:要求找出一个包含n个点的集合中距离最近的两个点。原本思想是我们应该去比较两点之间的欧几里得距离,而实际上,我们可以去比较它们的平方,这样,我们就可以避免对平方根的近似求解。
代码实现:
算法分析:
该算法的基本操作是求平方,每次求距离的平方值时,都要进行进行两次该操作。该算法属于θ(n2)。
3.3.2 凸包问题
凸集合:对于平面上的一个点集合(有限或无限),以集合中任意两点为端点的线段都属于该集合。
凸包:包含点集合的最小凸集合。
定理:任意包含n>2个点(不共线)的集合的凸包是以该集合中的某些点为顶点的凸多边形。
多边形的顶点称为“极点”。
凸包问题就是为一个有n个点的集合构造凸包。
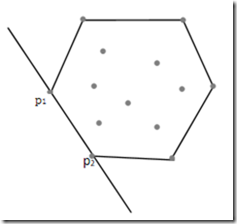
要解决这个问题,我们需考虑一些几何知识,若想构建凸包,我们就必须先找到极点,如果p1,p2为多边形的两个极点,这点集中的点必然是位于直线p1p2一侧或直线p1p2上的。所以在判断极点时,先要求出经过这两点的直线,设经过点p1(x1,y1),p2(x2,y2)的直线为ax+by=c(a=y2-y1,b=x1-x2,c=x1y2-x2y1),我们只需判断所有点集中的点是否全部满足ax+by<=c或ax+by>=c,若满足,则这两点为极点,若不满足,可以尝试其它点组合,直到遍历完所有两个点的组合。
代码实现:
算法分析:
它是属于θ(n3),可能上面的代码效率比这要略高一点,因为我利用了新的极点去查找下一个极点,所以中间跳过了一部分迭代过程,其实按照这个思想还可以进一步优化,比如查找到最后一个极点时,就可以直接返回集合,但我一直没想到怎样比较好地判断当前找到的新极点是否是最后一个极点,因为可能存在一种情况,就是很多点都在一条直线上,虽然这些点可能不是极点,但满足上面算法的思想,这也可能是算法不太完整的地方。







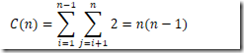
















 1719
1719

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








