怎么用计算机程序求根公式,一元四次方程求根公式

一元四次方程求根公式，是数学代数学基本公式，由意大利数学家费拉里首次提出证明。一元四次方程是未知数最高次数不超过四次的多项式方程，应用化四次为二次的方法，结合盛金公式求解。适用未知数最高次项的次数不大于四的多项式方程。其解法是受一元三次方程求解方法的启发而得到的。除最初解法外，该方程是还有其他简便解法。

中文名

一元四次方程求根公式

提出者

费拉里适用领域

未知数最高次数不超过四次的多项式方程

应用学科

数学代数，物理学

一元四次方程求根公式来源

编辑

语音

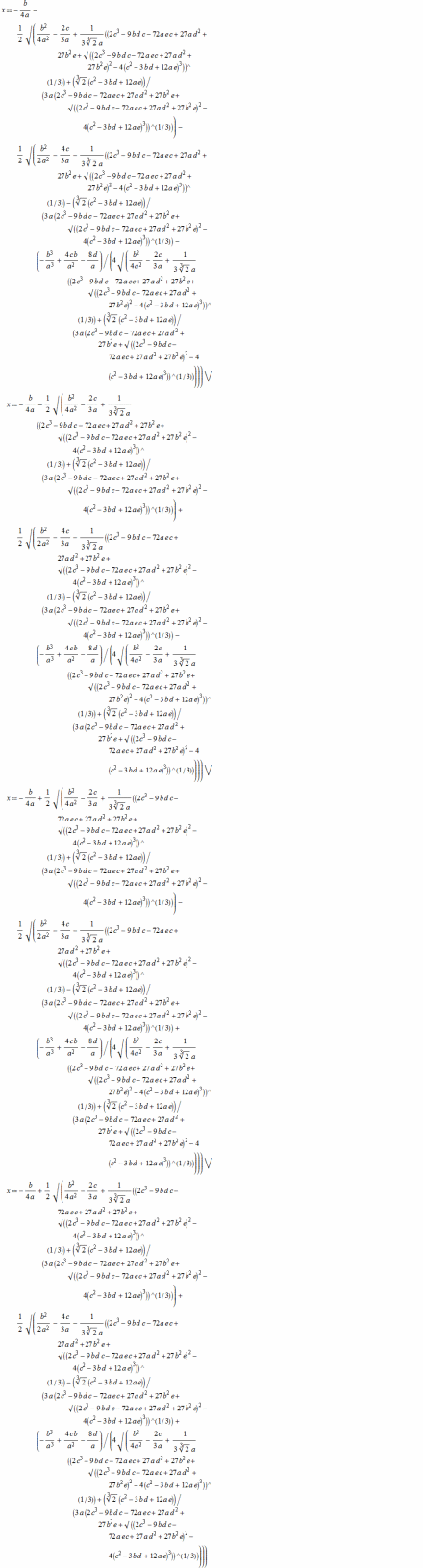
意大利数学家费拉里与一元四次方程的解法 卡当在《重要的艺术》一书中公布了塔塔利亚发现的一元三次方程求根公式之后，塔塔利亚谴责卡当背信弃义，提出要与卡当进行辩论与比赛。这场辩论与比赛在米兰市的教堂进行，代表卡当出场的是卡当的学生费拉里。 费拉里(Ferrari L.,1522~1565)出身贫苦，少年时代曾作为卡当的仆人。卡当的数学研究引起了他对数学的热爱，当其数学才能被卡当发现后，卡当就收他作了学生。 费拉里代替卡当与塔塔利亚辩论并比赛时，风华正茂，他不仅掌握了一元三次方程的解法，而且掌握了一元四次方程的解法，因而在辩论与比赛中取得了胜利，并由此当上了波伦亚大学的数学教授。 一元四次方程的求解方法，是受一元三次方程求解方法的启发而得到的。一元三次方程是在进行了巧妙的换元之后，把问题归结成了一元二次方程从而得解的。于是，如果能够巧妙地把一元四次方程转化为一元三次方程或一元二次方程，就可以利用已知的公式求解了。

一元四次方程求根公式费拉里法

编辑

语音

费拉里的方法是这样的：方程两边同时除以最高次项的系数可得 x^4+bx^3+cx^2+dx+e=0 (1)移项可得 x^4+bx^3=-cx^2-dx-e (2) 两边同时加上(1/2bx)^2 ，可将(2)式左边配成完全平方，方程成为 (x^2+1/2bx)^2=(1/4b^2-c)x^2-dx-e (3) 在(3)式两边同时加上(x^2+1/2bx)y+1/4y^2 可得 [(x^2+1/2bx)+1/2y]^2= (1/4b^2-c+y)x^2+(1/2by-d)x+1/4y^2-e (4) (4)式中的y是一个参数。当(4)式中的x为原方程的根时，不论y取什么值，(4)式都应成立。特别，如果所取的y值使(4)式右边关于x的二次三项式也能变成一个完全平方式，则对(4)对两边同时开方可以得到次数较低的方程。 为了使(4)式右边关于x的二次三项式也能变成一个完全平方式，只需使它的判别式变成0，即 (1/2by-d)^2-4(1/4b^2-c+y)(1/4y^2-e)=0 (5) 这是关于y的一元三次方程，可以通过塔塔利亚公式来求出y应取的实数值。 把由(5)式求出的y值代入(4)式后，(4)式的两边都成为完全平方，两边开方，可以得到两个关于x的一元二次方程。解这两个一元二次方程，就可以得出原方程的四个根。 费拉里发现的上述解法的创造性及巧妙之处在于：第一次配方得到(3)式后引进参数y，并再次配方把(3)式的左边配成含有参数y的完全平方，即得到(4)式，再利用(5)式使(4)的右边也成为完全平方，从而把一个一元四次方程的求解问题化成了一个一元三次方程及两个一元二次方程的求解问题。

误用：

不幸的是，就象塔塔利亚发现的一元三次方程求根公式被误称为卡当公式一样，费拉里发现的一元四次方程求解方法也曾被误认为是波培拉发现的。

一元四次方程求根公式置换群法

编辑

语音

解法见图片

说明：X1，X2，X3是某个三次方程的对称多项式(X1+X2+X3，X1*X2+X2*X3+X3*X1，X1*X2*X3均可求)，利用三次方程求根公式解出X1,X2,X3；又有X=x1+x2+x3+x4=ω1，接下来根据X,X1,X2,X3解x1,x2,x3,x4

一元四次方程求根公式天珩公式

编辑

语音

受费拉里法等一元四次方程求根公式的启发，沈天珩对公式进行了简化，并给出了更方便判断方程实数解个数和重根情况的判别法则。且天珩公式中不存在任何虚数开方的情况，使运算更为简单方便，也能借此简化计算机求根工具的代码。以下是完整公式：

一般式：

重根判别式：

总判别式：

(1)当D=E=F=0时，方程有一个四重实根。

(2)当DEF≠0，A=B=C=0时，方程有四个实根，其中有一个三重根。

(3)当E=F=0，D≠0时，方程有两对二重根；若D>0，根为实数；若D<0，根为虚数。

(4)当ABC≠0，Δ=0时，方程有一对二重实根；若AB>0，则其余两根为不等实根；若AB<0，则其余两根为共轭虚根。

(5)当Δ>0时，方程有两个不等实根和一对共轭虚根。

令

则有：

其中，sgn表示符号因子。计算方法如下：

<1>当n=0时，sgn(n)=0。

<2>当n≠0时，sgn(n)=abs(n)/n，即 (下同)

(6)当Δ<0时，若D与F均为正数，则方程有四个不等实根；否则方程有两对不等共轭虚根。

令

<1>若E=0,D>0,F>0，

<2>若E=0,D<0,F>0，

<3>若E=0,F<0，

<4>若E≠0，一定存在；故若D或F中有非正值即方程无实数解时，，而始终为正。

此时有：

当D与F均为正时，四实根为：

当D或F中有非正值时，四虚根为：

公式中的总判别式与三次方程盛金公式中的以及二次方程求根公式中的极为相似，体现了数学中的有序、对称、和谐与简洁美。

一元四次方程求根公式费拉里法求根公式

编辑

语音

[1]

[1]

四次方程 的求根公式过于复杂。为了描述方便，不得不借助几个中间变量。

或 (取模较大的数值)

(若 u 为零，则 v 也取值为零)

上面三个公式中，k 可取值 1,2,3。(m,S,T)的取值最好选择 最大的一组，这样计算 T 时数值最稳定。如果三个 均为零，则上面三个变量按下面三个公式取值

四个根为(下式中 )

一元四次方程求根公式其它证明方法

编辑

语音

维基百科上有一个非常复杂的公式。

它是方程 的四个根。将其拆分后，可得：

四个根为(下式中 )

可见，这个公式是“求根公式(费拉里法)”的一个特例。这个公式不仅复杂、难用，而且还不能处理 m = 0 的情况，如：求解方程 (等价于方程 )时会失败。

词条图册

更多图册

参考资料

1.

中华人民共和国教育部．数学书：未知，2003