codeforces 765 D Artsem and Saunders

最新推荐文章于 2025-09-11 19:19:55 发布

weixin_34342207

最新推荐文章于 2025-09-11 19:19:55 发布

阅读量148

点赞数

CC 4.0 BY-SA版权

文章标签：数据结构与算法

原文链接：http://www.cnblogs.com/Mrleon/p/9098848.html

本文探讨了一道关于函数构造的问题，通过分析给定函数f[x]，寻找满足特定条件的函数g(x)和h(x)。利用并查集算法进行节点连接，确保函数的正确构造，并检查生成的函数是否符合题目要求。

传送门

题意：给你一个函数f[x]，问你是否存在满足 g(h(x)) = x for all 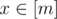$\text{[math]}$ , and h(g(x)) = f(x) for all $\text{[math]}$ , 的两个函数

题解：先化简公式得到一个构造g（x）的公式,g(x)=g(f(x))，并查集将x和f（x）捆绑起来，然后for一遍g（x）这个函数，将属于同一个集团里面的编上相同的号码，然后推出公式h(x)=f(h(x))得到h（x）函数的值，最后用题目条件分别check一下生成的函数

#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <map>
#include <queue>
#include <vector>
#include <cstring>
#include <iomanip>
#include <set>
#include<ctime>
#include<unordered_map>
//CLOCKS_PER_SEC
#define se second
#define fi first
#define ll long long
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define Pii pair<int,int>
#define Pli pair<ll,int>
#define ull unsigned long long
#define pb push_back
#define fio ios::sync_with_stdio(false);cin.tie(0)
const int N=1e6+10;
const ull base=163;
const int INF=0x3f3f3f3f;
using namespace std;
int f[N],g[N],h[N];
int fa[N];
int F(int x){
    return fa[x]==x?x:fa[x]=F(fa[x]);
}
map<int,int>mp;
int main(){
    fio;
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>f[i];
    }
    for(int i=1;i<=N-5;i++)fa[i]=i;
    for(int i=1;i<=n;i++){
        int u=i,v=f[i];
        u=F(i),v=F(v);
        if(u!=v){
            fa[u]=v;
        }
    }
    int m=0;
    for(int i=1;i<=n;i++){
        if(!mp[F(f[i])]){
            mp[F(f[i])]=++m;
        }
        g[i]=mp[F(f[i])];
    }
    for(int i=1;i<=n;i++){
        h[g[i]]=f[i];
    }
    for(int i=1;i<=n;i++){
        if(h[g[i]]!=f[i]){
            return cout<<-1,0;
        }
    }
    for(int i=1;i<=m;i++){
        if(g[h[i]]!=i){
            return cout<<-1,0;
        }
    }
    cout<<m<<endl;
    for(int i=1;i<=n;i++){
        cout<<g[i]<<" ";
    }
    cout<<endl;;
    for(int i=1;i<=m;i++){
        cout<<h[i]<<" ";
    }
    return 0;
}