浅谈期望dp

 今天解决了一直以来的一个疑问：

为什么期望dp需要倒推？

参考：传送门

例题：传送门

每个格子可以向左右或向下或原地不动。

假如正序推式子：

且dp设置成从(x,y)到(i,j)的期望值，那么：

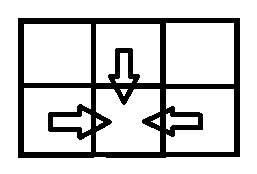
当前状态的值将由这四个位置的状态值得到，那么概率怎么求？？？

这四个位置到当前状态的概率可不是1/4。。。

那么对应的期望也不是很好办。

期望，状态设置应保证已知最终状态如何表示。

我们这里将f[i][j]表示为从(i,j)到最后一行的状态，这样最终答案也确定为f[x][y].

继续看转移：

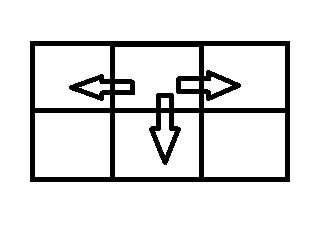
 从当前点向后转移时，具体得到哪几个位置和概率就很好算了。

这样的话f[i][j] = 1/4*(f[i+1][j]+f[i][j]+f[i][j+1]+f[i][j-1]);

我们需要倒序求式子，使每次到当前行时，f[i+1][j]作为常数参与消元。

emmm...

没了。

再有一些感触会加以补充的。

转载于:https://www.cnblogs.com/ve-2021/p/11054891.html