[线段树][数学]JZOJ 4237 Melancholy

Description

DX3906星系，Melancholy星上，我在勘测这里的地质情况。
我把这些天来已探测到的区域分为N组，并用二元组(D,V)对每一组进行标记：其中D为区域的相对距离，V为内部地质元素的相对丰富程度。
在我的日程安排表上有Q项指派的计划。每项计划的形式是类似的，都是“对相对距离D在[L,R]之间的区域进行进一步的勘测，并在其中有次序地挑出K块区域的样本进行研究。”采集这K块的样品后，接下来在实验中，它们的研究价值即为这K块区域地质相对丰富程度V的乘积。
我对这Q项计划都进行了评估：一项计划的评估值P为所有可能选取情况的研究价值之和。
但是由于仪器的原因，在一次勘测中，这其中V最小的区域永远不会被选取。
现在我只想知道这Q项计划的评估值对2^32取模后的值，特殊地，如果没有K块区域可供选择，评估值为0。

 

Input

第一行给出两个整数，区域数N与计划数Q。
第二行给出N个整数，代表每一块区域的相对距离D。
第三行给出N个整数，代表每一块区域的内部地质元素的相对丰富程度V。
接下来的Q行，每一行3个整数，代表相对距离的限制L,R，以及选取的块数K。

Output

输出包括Q行，每一行一个整数，代表这项计划的评估值对2^32取模后的值。

 

Sample Input

5 3
5 4 7 2 6
1 4 5 3 2
6 7 1
2 6 2
1 8 3

Sample Output

5
52
924

 

Data Constraint

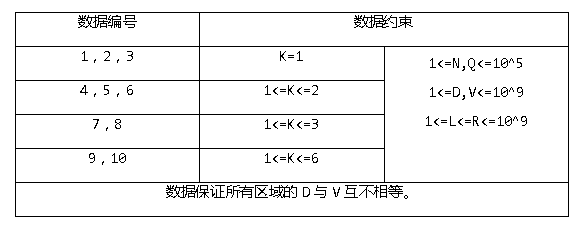
分析

我们离散以后建线段树，然后剔除最小值也很简单，把最小值的位置找出来，求l,pos-1;pos+1,r的值就行了

然后值=∑_i=1leftval[i]+right[val][i]  +∑_i=1^i<=6∑_j=1^j<ileftval[j]*rightval[i-j]

 

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <memory.h>
using namespace std;
#define lson t[x].l
#define rson t[x].r
typedef unsigned int ll;
const int N=1e5+10;
struct Area {
    ll d,v;
    bool operator < (const Area a) const {
        return d<a.d;
    }
}a[N];
struct Seg {
    int l,r,pos;
    ll min,sum[7];
}t[4*N];
int cnt,rt;
int tpos;
ll tmin,b[2][7],ans[7],l,r;
int n,q,k;

inline void Build(int &x,int l,int r) {
    if (!x) x=++cnt;
    if (l==r) {
        t[x].min=t[x].sum[1]=a[l].v;t[x].pos=l;
        return;
    }
    register int mid=l+r>>1;
    Build(lson,l,mid);Build(rson,mid+1,r);
    t[x].min=min(t[lson].min,t[rson].min);
    t[x].pos=t[x].min==t[lson].min?t[lson].pos:t[rson].pos;
    for (register int i=1;i<=6;i++) t[x].sum[i]=t[lson].sum[i]+t[rson].sum[i];
    for (register int i=1;i<=6;i++)
        for (register int j=1;j<i;j++) t[x].sum[i]+=t[lson].sum[j]*t[rson].sum[i-j];
}

inline void Get_Min(int x,int l,int r,int xl,int xr) {
    if (xl<=l&&r<=xr) {
        if (tmin>t[x].min) tmin=t[x].min,tpos=t[x].pos;
        return;
    }
    register int mid=l+r>>1;
    if (xl<=mid) Get_Min(lson,l,mid,xl,xr);
    if (mid<xr) Get_Min(rson,mid+1,r,xl,xr);
}

inline void Query(int x,int l,int r,int xl,int xr,int side) {
    if (l>r||l>xr||xl>r||xl>xr) return;
    if (xl<=l&&r<=xr) {
        ll c[7]={0,0,0,0,0,0,0};
        for (register int i=1;i<=6;i++) c[i]=b[side][i]+t[x].sum[i];
        for (register int i=1;i<=6;i++)
            for (register int j=1;j<i;j++) c[i]+=b[side][j]*t[x].sum[i-j];
        memcpy(b[side],c,sizeof c);
        return;
    }
    register int mid=l+r>>1;
    if (xl<=mid) Query(lson,l,mid,xl,xr,side);
    if (mid<xr) Query(rson,mid+1,r,xl,xr,side);
}

inline void Solve() {
    l=lower_bound(a+1,a+n+1,(Area){l,0})-a;
    r=upper_bound(a+1,a+n+1,(Area){r,0})-a-1;
    if (r-l<k) {
        printf("0\n");
        return;
    }
    if (l>=r) {
        printf("0\n");
        return;
    }
    tmin=2147483647u;tpos=-1;
    Get_Min(rt,1,n,l,r);
    memset(b,0,sizeof b);
    Query(rt,1,n,l,tpos-1,0);Query(rt,1,n,tpos+1,r,1);
    for (register int i=1;i<=6;i++) ans[i]=b[0][i]+b[1][i];
    for (register int i=1;i<=6;i++)
        for (int j=1;j<i;j++) ans[i]+=b[0][j]*b[1][i-j];
    for (register int i=1;i<=k;i++) ans[k]*=i;
    printf("%u\n",ans[k]);
}

int main() {
    scanf("%d%d",&n,&q);
    for (int i=1;i<=n;i++) scanf("%d",&a[i].d);
    for (int i=1;i<=n;i++) scanf("%d",&a[i].v);
    sort(a+1,a+n+1);
    Build(rt,1,n);
    for (int i=1;i<=q;i++) {
        scanf("%d%d%d",&l,&r,&k);
        Solve();
    }
}

View Code

 

转载于:https://www.cnblogs.com/mastervan/p/10331709.html