∪ 并集
∩ 交集
∅ 空集
lim 表示极限
∑ 求和符号
Log以e为底,a得对数
e^lna=a
∂读作round 法国人发明的。
通常我们读作“偏”就好勒,
例如,∂z/∂x,读作 偏z比去偏x.
(u+v)'=u'+v'
c'=0(c为常数)
(x^a)'=ax^(a-1),a为常数且a≠0
(a^x)'=a^xlna
(e^x)'=e^x
(logax)'=1/(xlna),a>0且 a≠1
(lnx)'=1/x
(uv)'=uv'+u'v
(u/v)'=(u'v-uv')/v^2
||W||1=L1
||W||2=L2
sign(x) 函数是个符号函数
当x>0,sign(x)=1;
当x=0,sign(x)=0;
当x<0, sign(x)=-1;
损失函数(loss function)
平方损失(Square loss)
如果是Hinge Loss,那就是著名的SVM了;
如果是exp-Loss,那就是牛逼的 Boosting了;
如果是log-Loss,那就是Logistic Regression了
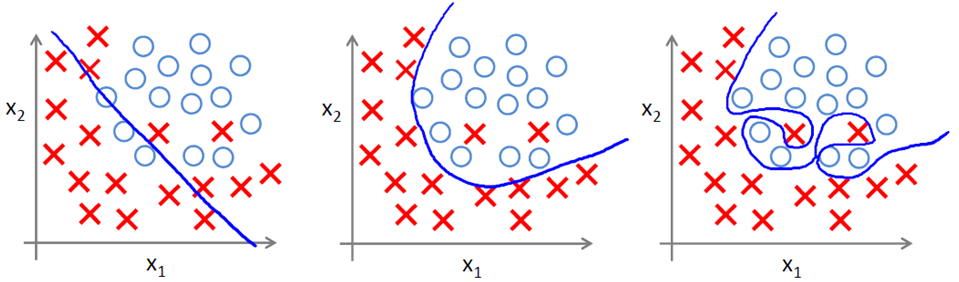
左图线性、中间多项式、有图更复杂的多项式
左图(欠拟合): 分类的结果明显有点欠缺,有很多的“男人”被分类成了“女人”。分类模型可以用 f(x) = g(w0+w1x1+w2x2)来表示。
中图: 虽然有两个点分类错误,但也能够解释,毕竟现实世界中总有例外,或者是有噪音干扰,比如有些人男人留长发、花招,或者属于是雌雄同体... ...分类模型可能是类似f(x) = g(w0+w1x1+w2x2+w3x12+w4x22+w5x1x2)这样的形式。
右图(过拟合): 分类结果全部正确,但是这个分类模型似乎也有问题——过犹不及,连“人妖”都能识别出来,可想而知,学习的时候需要更多的参数项(也就是要收集更多的特征,例如生殖器官的情况、喉结的大小、说话声音的粗细等等)。总而言之f(x)多项式的项数特别多,因为需要提供的特征多。或者是在提供的数据集中使用到的特征非常多(一般而言,机器学习的过程中,所提供的很多特征未必都要被用到)。
L1正则化是指权值向量w中各个元素的绝对值之和,通常表示为||w||1 L2正则化是指权值向量w中各个元素的平方和然后再求平方根(可以看到Ridge回归的L2正则化项有平方符号),通常表示为||w||2
一般都会在正则化项之前添加一个系数,Python中用α表示,一些文章也用λ表示。这个系数需要用户指定。
那添加L1和L2正则化有什么用?下面是L1正则化和L2正则化的作用,这些表述可以在很多文章中找到。
L1正则化可以产生稀疏权值矩阵,即产生一个稀疏模型,因此可以用于特征选择 L2正则化可以防止模型过拟合(overfitting);一定程度上,L1也可以防止过拟合
稀疏模型与特征选择
上面提到L1正则化有助于生成一个稀疏权值矩阵,进而可以用于特征选择。为什么要生成一个稀疏矩阵?
稀疏矩阵指的是很多元素为0,只有少数元素是非零值的矩阵,即得到的线性回归模型的大部分系数都是0. 通常机器学习中特征数量很多,例如文本处理时,如果将一个词组(term)作为一个特征,那么特征数量会达到上万个(bigram)。在预测或分类时,那么多特征显然难以选择,但是如果代入这些特征得到的模型是一个稀疏模型,表示只有少数特征对这个模型有贡献,绝大部分特征是没有贡献的,或者贡献微小(因为它们前面的系数是0或者是很小的值,即使去掉对模型也没有什么影响),此时我们就可以只关注系数是非零值的特征。这就是稀疏模型与特征选择的关系。
L2函数分析
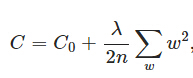
C0代表原始的代价函数,后面那一项就是L2正则化项。它是这样来的:全部參数w的平方的和,除以训练集的样本大小n。
λ就是正则项系数,权衡正则项与C0项的比重。另外另一个系数1/2,1/2经常会看到,主要是为了后面求导的结果方便,后面那一项求导会产生一个2。与1/2相乘刚好凑整。
L2正则化项是怎么避免overfitting的呢?我们推导一下看看,先求导:
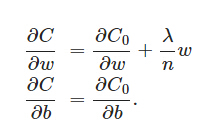




 本文介绍了常用的数学符号及其在机器学习中的应用,包括集合运算、微积分基础、正则化概念及其作用,并通过实例解释了欠拟合与过拟合的区别。
本文介绍了常用的数学符号及其在机器学习中的应用,包括集合运算、微积分基础、正则化概念及其作用,并通过实例解释了欠拟合与过拟合的区别。

















 274
274

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








