之前那篇文章里提到,L1其实是加上服从拉普拉斯分布的先验,L2是加上服从高斯分布的先验:
http://www.cnblogs.com/charlesblc/p/7977732.html
那么记住拉普拉斯的公式和高斯的公式:
拉普拉斯(Laplace)

高斯(Gaussian)分布
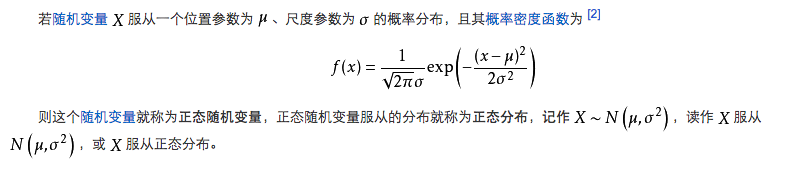
之前那篇文章里提到,L1其实是加上服从拉普拉斯分布的先验,L2是加上服从高斯分布的先验:
http://www.cnblogs.com/charlesblc/p/7977732.html
那么记住拉普拉斯的公式和高斯的公式:

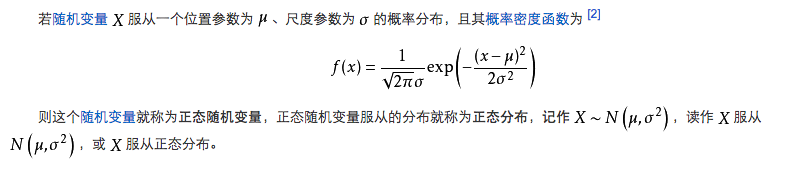

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


