n个元素的入栈顺序有多少种出栈顺序？

问题：w1、w2、w3、w4、w5，5个元素将会按顺序入栈，求出栈顺序有多少种情况。

先写一下结论方便记忆：

1个元素：1种

2个元素：2种

3个元素：5种

4个元素：14种

5个元素：42种

简单的分析过程如下：

 

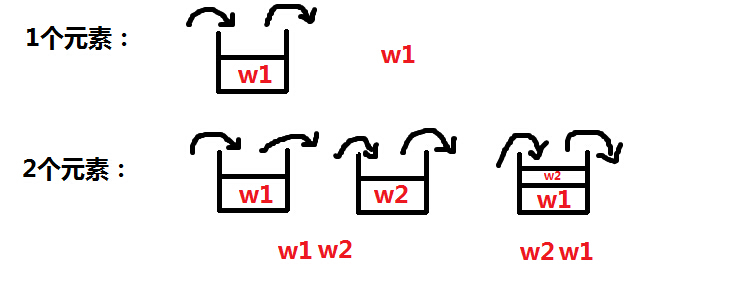
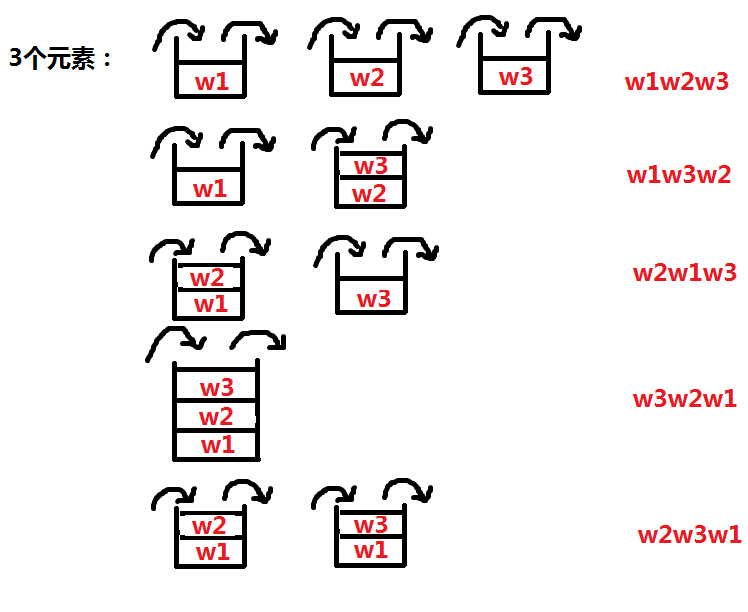
n个数据依次入栈，出栈顺序种数的递推公式如下：
F(n)=∑(F(n-1-k)*Fk);其中k从0到n-1

已知F0=1,
F1=F0*F0=1
F2=F1*F0+F0*F1=2
F3=F2*F0+F1*F1+F0*F2=5
F4=F3*F0+F2*F1+F1*F2+F0*F3=14
F5=F4*F0+F3*F1+F2*F2+F1*F3+F0*F4=42
很容易发现，正好是对称关系

 

转载于:https://www.cnblogs.com/gongxing/p/4823212.html