机器学习算法中的偏差-方差权衡(Bias-Variance Tradeoff)

简单的以下面曲线拟合例子来讲：

 

直线拟合后，相比原来的点偏差最大，最后一个图完全拟合了数据点偏差最小；但是拿第一个直线模型去预测未知数据，可能会相比最后一个模型更准确，因为最后一个模型过拟合了，即第一个模型的方差比最后一个模型小。一般而言高偏差意味着欠拟合，高方差意味着过拟合。他们之间有如下的关系：              本文地址

                                          

 

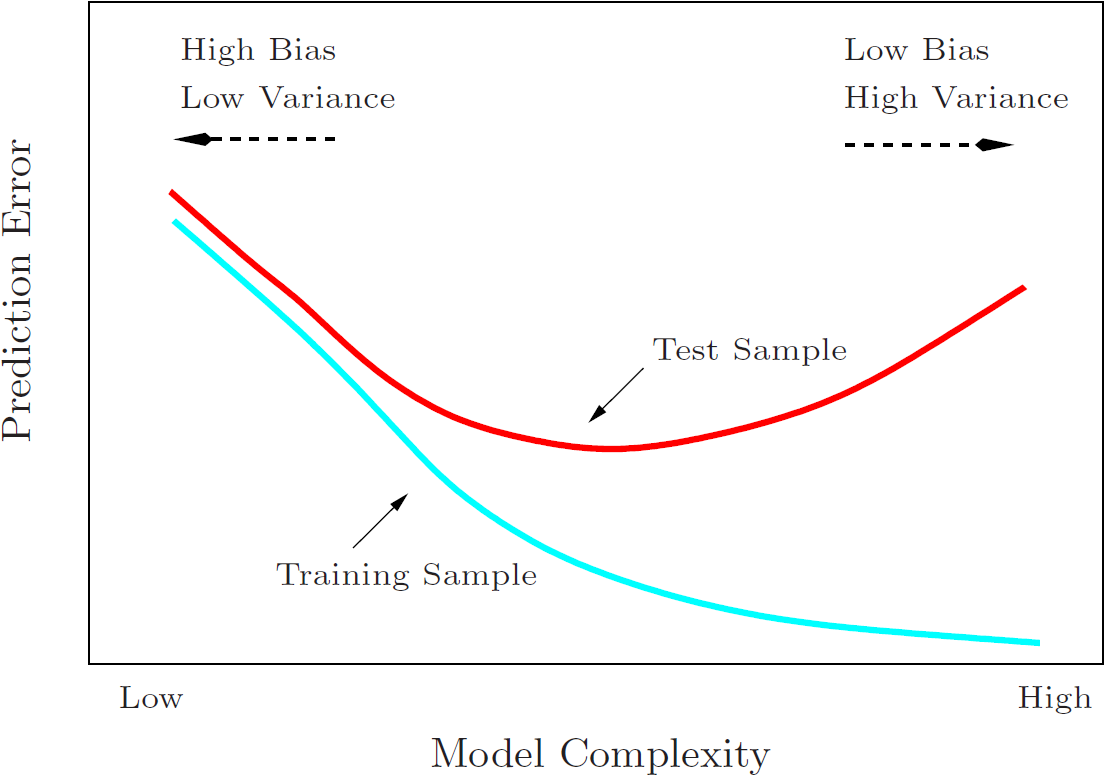
本文转自tenos博客园博客，原文链接：http://www.cnblogs.com/TenosDoIt/p/3712590.html，如需转载请自行联系原作者