贝叶斯先验解释l1正则和l2正则区别

这里讨论机器学习中L1正则和L2正则的区别。

在线性回归中我们最终的loss function如下：

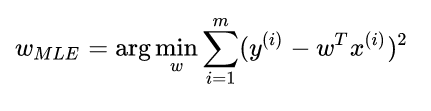
那么如果我们为w增加一个高斯先验，假设这个先验分布是协方差为 的零均值高斯先验。我们在进行最大似然：

 

 

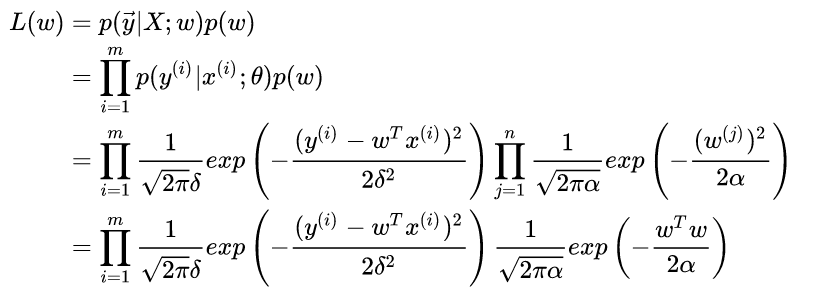
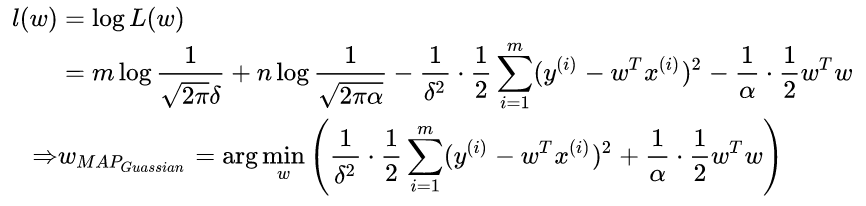
这个东西不就是我们说的加了L2正则的loss function吗？

 同理我们如果为w加上拉普拉斯先验，就可以求出最后的loss function也就是我们平时说的加了L1正则：

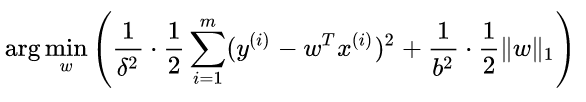
因为拉普拉斯的分布相比高斯要更陡峭，它们的分布类似下图，红色表示拉普拉斯，黑色表示高斯

 

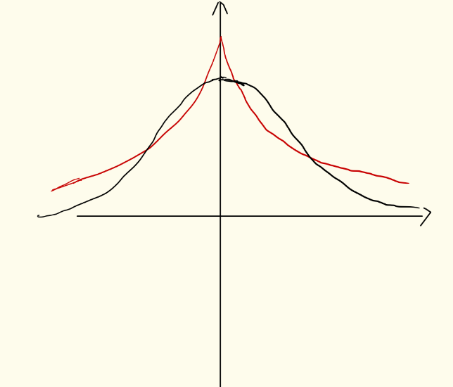
可以看出拉普拉斯的小w的数目要比高斯的多，w的分布陡峭，而高斯的w分布较为均匀。也就是说，l1正则化更容易获得稀疏解，还可以挑选重要特征。l2正则有均匀化w的作用。

转载于:https://www.cnblogs.com/dylan9/p/8716839.html