一道有趣的GOOGLE面试题

最新推荐文章于 2025-08-21 09:38:50 发布

转载最新推荐文章于 2025-08-21 09:38:50 发布 · 83 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：https://my.oschina.net/jiaozg/blog/91058

文章标签：

#面试 #数据结构与算法 #java

本文介绍了一种在O(n)时间复杂度与O(1)空间复杂度下寻找数组中重复元素的方法。通过一种类似基数排序的技术，巧妙地解决了常规哈希表方法在空间复杂度上的不足。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

为什么80%的码农都做不了架构师？>>>

问题： 一个大小为n的数组，里面的数都属于范围[0, n-1]，有不确定的重复元素，找到至少一个重复元素，要求O(1)空间和O(n)时间。

这个题目要求用O(n)的时间复杂度，这意味着只能遍历数组一次。同时还要寻找重复元素，很容易想到建立哈希表来完成，遍历数组时将每个元素映射到哈希表中，如果哈希表中已经存在这个元素则说明这就是个重复元素。因此直接使用C++ STL中的hash_set，可以方便的在O(n)时间内完成对重复元素的查找。

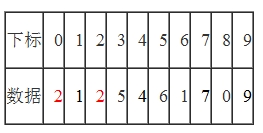
但是题目却在空间复杂度上有限制——要求为O(1)的空间。因此采用哈希表这种解法肯定在空间复杂度上是不符合要求的。但可以沿着哈希法的思路继续思考，题目中数组中所以数字都在范围[0， n-1]，因此哈希表的大小为n即可。因此我们实际要做的就是对n个范围为0到n-1的数进行哈希，而哈希表的大小刚好为n。对排序算法比较熟悉的同学不难发现这与一种经典的排序算法——基数排序非常类似。而基数排序的时间空间复杂度刚好符合题目要求！因此尝试使用基数排序来解这道面试题。

package algorithm;

public class RadixSort {

public static final int NO_REPEAT_FLAG = -1;

// 类似于基数排序，找出数组中第一个重复元素。
public static int radixSort(int[] a, int n) {
	int i = 0;

	while (i != a[i]) {
		if (a[i] == a[a[i]]) {
			return a[i];
		} else {
			int t = a[i];
			a[i] = a[a[i]];
			a[t] = t;
		}
	}

	return NO_REPEAT_FLAG;
}

private static void printArray(int[] a, int n) {
	for (int i = 0; i < n; i++) {
		System.out.print(a[i]);
	}
	System.out.println();
}

public static void main(String[] args) {
	int max = 10;
	int[] a = { 2, 4, 1, 5, 7, 6, 1, 9, 0, 2 };

	System.out.println("数组为：");
	printArray(a, max);

	int repeatNumber = radixSort(a, max);
	if (repeatNumber != NO_REPEAT_FLAG) {
		System.out.println("重复元素为： " + repeatNumber);
	} else {
		System.out.println("没有重复元素");
	}
}

}

输出：

数组为： 2415761902 重复元素为： 2

转载于:https://my.oschina.net/jiaozg/blog/91058