- 概率密度与分布函数
当用函数f(x)来表示连续型随机变量时,我们将f(x)称为概率密度函数(或者密度函数 )
想要求随机变量的概率,可以用
分布函数F(x)来表示,

F(x)为图中阴影部分

如:
F(2)=P(X<=2),就是上图黑色部分的阴影面积
P(2<X<6)=F(6)-F(2),就是6的面积减去2的面积得到红色阴影部分
密度函数的性质及与分布函数的关系

5、
P(X=X)是在连续分布条件下为概率为0,因为只是某个点的话,分布函数面积为0,
这样导致在函数运算中>=跟>,<=跟<其实是一样的
连续型随机变量的期望值与方差定义

- 正态分布
1、正态分布的定义及图像特点
如果随机变量X的概率密度

则称X服从正态分布,记作X~N(μ,
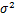 ),其中,-
),其中,- 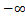 <μ<
<μ<
 ,μ为随机变量X的均值,
,μ为随机变量X的均值,
 为随机变量X的标准差,读作西格玛,随机变量X,服从均值为μ,方差为
为随机变量X的标准差,读作西格玛,随机变量X,服从均值为μ,方差为
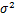 的正态分布
的正态分布
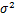 ),其中,-
),其中,- 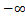 <μ<
<μ<
 ,μ为随机变量X的均值,
,μ为随机变量X的均值,
 为随机变量X的标准差,读作西格玛,随机变量X,服从均值为μ,方差为
为随机变量X的标准差,读作西格玛,随机变量X,服从均值为μ,方差为
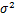 的正态分布
的正态分布
2、f(x)的特性
a、f(x)>=0
b、曲线f(x)相对于x=μ对称,并在x=μ处达到最大值,如下

c、
 越大,曲线越平缓,
越大,曲线越平缓,
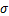 越小,曲线越陡峭
越小,曲线越陡峭
 越大,曲线越平缓,
越大,曲线越平缓,
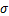 越小,曲线越陡峭
越小,曲线越陡峭
d、当x趋于无穷式,曲线以x轴为其渐进线
3、标准正态分布
当μ=0,
 =1时,有标准正态分布N(0,1)如下
=1时,有标准正态分布N(0,1)如下
 =1时,有标准正态分布N(0,1)如下
=1时,有标准正态分布N(0,1)如下

对于标准正态
分布,通常有
 表示概率密度函数,
表示概率密度函数,  表示分布函数
表示分布函数
 表示概率密度函数,
表示概率密度函数,  表示分布函数
表示分布函数

4、标准正态分布的重要特性
设X~N(μ,
 ),则有
),则有
 ),则有
),则有

将一般的正态分布转化为标准正态分布公式
5、正态分布概率计算
a、通过将正态分布转化为标准正态分布,通过查表,就可以解决正态分布的概率计算
b、负值的x,可由此得 到

计算案例





 本文介绍了概率密度函数和分布函数的概念,详细解释了连续型随机变量的概率计算方法。此外,还深入探讨了正态分布的定义、图像特点及其转换为标准正态分布的方法。
本文介绍了概率密度函数和分布函数的概念,详细解释了连续型随机变量的概率计算方法。此外,还深入探讨了正态分布的定义、图像特点及其转换为标准正态分布的方法。

















 293
293

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








