《算法导论》学习笔记——归并排序

归并排序

1.分治法

  很多算法在结构上都是递归的，为了解决一个问题，算法一次或多次递归地调用其自身已解决紧密相关的若干子问题。这就是分治法的思想。

  分治法是一种很重要的算法。字面上的解释是“分而治之”，就是把一个复杂的问题分成两个或更多的相同或相似的子问题，再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并。

  分治模式在每层递归时都有三个步骤：
  - 分解原问题为若干子问题，这些子问题是原问题规模较小的实例；
  - 解决这些子问题，调用上一步骤，若子问题规模足够小，直接求解即可；
  - 合并这些子问题的解成原问题的解。

2.归并排序

  归并算法完全遵循上述分治策略，算法流程如下：
  - 分解：分解待排序的n个元素序列成各具n/2元素的两个子序列；
  - 解决：使用归并排序递归地排序两个子序列；
  - 合并：合并两个已排序的子序列以产生已排序的答案。

  对于分治策略，有两个值得特别关注的地方：
  1. 确定子问题的最小规模，即明确递归算法的终止条件。以归并排序为例，当子数组包含元素个数为1时，即停止调用函数自身 。
  2. 递归“回升”的操作，当待排序的字数组包含元素为1时，在这种情况下开始合并各个子数组。

  归并排序的整个流程如下图所示：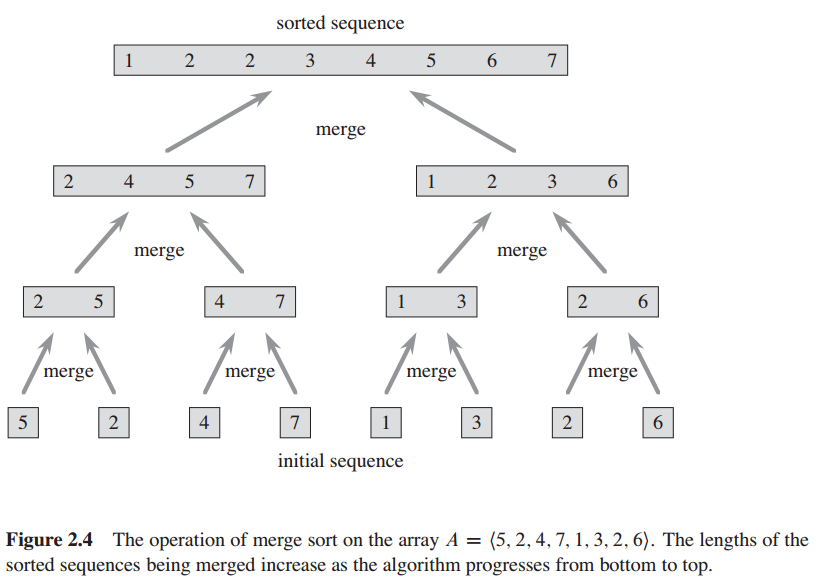

  最后对算法复杂度进行评价：归并排序的算法复杂度为O(nlogn)。

3.代码实现(C/C++,Java,Python)

C

#include <stdio.h>
#include <stdlib.h>

void merge_array(int* a, int first, int mid, int last) {
    int first1 = first, first2 = mid + 1;
    int last1 = mid, last2 = last;
    int index = 0, i;
    int *tmp;
    tmp = (int* )malloc((last - first + 1) * sizeof(int));
    if(tmp == NULL) exit(1);
    while(first1 <= last1 && first2 <= last2) {
        if(a[first1] <= a[first2]) 
            tmp[index++] = a[first1++];
        else 
            tmp[index++] = a[first2++];
    }
    while(first1 <= last1) 
        tmp[index++] = a[first1++];
    while(first2 <= last2) 
        tmp[index++] = a[first2++];
    for( i=0; i<(last-first+1); i++) 
        a[first + i] = tmp[i];
    free(tmp);
}

void merge_sort(int* a, int first, int last) {
    int mid = 0;
    if(first < last) {
        mid = (first + last) / 2;
        merge_sort(a, first, mid);
        merge_sort(a, mid + 1, last);
        merge_array(a, first, mid, last);
    }
}

int main() {
    int len, i;
    int *a;
    printf("Enter the length of array: ");
    scanf("%d", &len);
    a = (int *)malloc(sizeof(int) * len);
    printf("Enter the element of array: ");
    for(i = 0; i < len; i++)
        scanf("%d", &a[i]);
    merge_sort(a, 0, len-1);
    for(i = 0; i < len; i++)
        printf("%d ", a[i]);
    free(a);
    return 0;
}

C++

#include <iostream>
#include <vector>
using namespace std;

void merge_array(vector<int> &array, int first, int mid, int last) {
    int first1 = first, first2 = mid + 1;
    int last1 = mid, last2 = last;
    vector<int> tmp;
    while(first1 <= last1 && first2 <= last2) {
        if(array[first1] <= array[first2])
            tmp.push_back(array[first1++]);
        else
            tmp.push_back(array[first2++]);
    }
    while(first1 <= last1)
        tmp.push_back(array[first1++]);
    while(first2 <= last2)
        tmp.push_back(array[first2++]);
    for(int i = 0; i < (last - first + 1); i++)
        array[first + i] = tmp[i];
}

void merge_sort(vector<int> &array, int first, int last) {
    int mid = 0;
    if(first < last) {
        mid = (first + last) / 2;
        merge_sort(array, first, mid);
        merge_sort(array, mid + 1, last);
        merge_array(array, first, mid, last);
    }
}

void display(vector<int> &array){
    for(vector<int>::iterator it = array.begin(); it < array.end(); it++)
        cout << *it<< " ";
}  

int main() {
    vector<int> array;
    int length, element;
    cout << "Enter the length of array: ";
    cin >> length;
    cout << "Enter the element of array: ";
    for(int i = 0; i < length; i++) {
        cin >> element;
        array.push_back(element);
    }
    merge_sort(array, 0, length-1);
    display(array);
    return 0;
}

Java

import java.util.*;

public class MergeSort{
    public static void display(Iterator<Integer> it) {
        while(it.hasNext()) {
            Integer element = it.next();
            System.out.print(element + " ");
        }
    }
    public static void main(String[] args) {
        ArrayList<Integer> array = new ArrayList<Integer>();
        Scanner in = new Scanner(System.in);
        System.out.print("Entrt the length of array: ");
        int len = in.nextInt();
        for(int i = 0; i < len; i++)
            array.add(in.nextInt());
        in.close();
        Sort sort = new Sort(array);
        sort.mergeSort(array, sort.getFirst(), sort.getLast());
        display(array.iterator());
    }
}

class Sort{
    public Sort(ArrayList<Integer> array) {
        this.array = array;
    }

    public int getFirst() {
        return 0;
    }

    public int getLast() {
        return array.size() - 1;
    }

    public void mergeSort(ArrayList<Integer> array, int first, int last) {
        int mid = 0;
        if(first < last) {
            mid = (first + last) / 2;
            mergeSort(array, first, mid);
            mergeSort(array, mid + 1, last);
            mergeArray(array, first, mid, last);
        }
    }

    public void mergeArray(ArrayList<Integer> array, int first, int mid, int last) {
        int first1 = first, first2 = mid + 1;
        int last1 = mid, last2 = last;
        ArrayList<Integer> tmp = new ArrayList<Integer>();
        while(first1 <= last1 && first2 <= last2) {
            if(array.get(first1) <= array.get(first2)) {
                tmp.add(array.get(first1));
                first1++;
            }
            else {
                tmp.add(array.get(first2));
                first2++;
            }
        }
        while(first1 <= last1) {
            tmp.add(array.get(first1));
            first1++;
        }
        while(first2 <= last2) {
            tmp.add(array.get(first2));
            first2++;
        }
        for(int i = 0; i < (last - first + 1); i++)
            array.set(first + i, tmp.get(i));
    }

    private ArrayList<Integer> array;
}

Python

Merge_Sort.py

def merge_sort(a, first, last):
    if first < last:
    mid = (first + last) / 2
        merge_sort(a, first, mid)
        merge_sort(a, mid + 1, last)
        merge_array(a, first, mid, last)

def merge_array(a, first, mid, last):
    first1 = first
    last1 = mid
    first2 = mid + 1
    last2 = last
    tmp = []
    while first1 <= last1 and first2 <= last2:
        if a[first1] <= a[first2]:
            tmp.append(a[first1])
            first1 += 1
        else:
             tmp.append(a[first2])
            first2 += 1
    while first1 <= last1:
        tmp.append(a[first1])
        first1 += 1
    while first2 <= last2:
        tmp.append(a[first2])
        first2 += 1
    for i in range(0, last - first + 1):
        a[first + i] = tmp[i]

test.py

import Merge_Sort

a = [3, 5, 4, 2, 6, 1, 0, 7]
length = len(a)
Merge_Sort.merge_sort(a, 0, length - 1)
print a

转载于:https://www.cnblogs.com/zhxbao/p/merge_sort.html