背包问题总结

最新推荐文章于 2024-05-12 21:14:22 发布
最新推荐文章于 2024-05-12 21:14:22 发布
阅读量162 收藏
点赞数
CC 4.0 BY-SA版权
文章标签： php 数据结构与算法
原文链接：https://my.oschina.net/lin546/blog/1619880

为什么80%的码农都做不了架构师？>>>   hot3.png

01背包

不死族的巫妖王发工资拉,死亡骑士拿到一张N元的钞票(记住,只有一张钞票),为了防止自己在战斗中频繁的死掉,他决定给自己买一些道具,于是他来到了地精商店前.

死亡骑士:"我要买道具!"

地精商人:"我们这里有三种道具,血瓶150块一个,魔法药200块一个,无敌药水350块一个."

死亡骑士:"好的,给我一个血瓶."

说完他掏出那张N元的大钞递给地精商人.

地精商人:"我忘了提醒你了,我们这里没有找客人钱的习惯的,多的钱我们都当小费收了的,嘿嘿."

死亡骑士:"......你妹"

死亡骑士想,与其把钱当小费送个他还不如自己多买一点道具,反正以后都要买的,早点买了放在家里也好,但是要尽量少让他赚小费.


现在死亡骑士希望你能帮他计算一下,最少他要给地精商人多少小费.

上面就是一个01背包问题。上面的问题可以描述为：

有n个物品，每个物品的重量为weight[i]，每个物品的价值为value[i]。现在有一个背包，它所能容纳的重量为total，问：当你面对这么多有价值的物品时，你的背包所能带走的最大价值是多少？


思路：每个物品无非是装入背包或者不装入背包，那么就一个一个物品陆续放入背包中。可以有

tab[i][j] = max(tab[i-1][j-weight[i]]+value[i],tab[i-1][j]) ({i,j|0<i<=n,0<=j<=total})

其中i表示放第i个物品，j表示背包所容纳的重量，那么tab[i-1][j-weight[i]]+value[i]表示放入第i物品，刚开始接触会有疑问，tab[i-1][j-weight[i]]这个值，可以这样理解：tab[i-1][j]为装到上一个物品在背包j容量时的最佳值，那么如果我要求在j容量的时候放入现在的i物品的价值，那么是不是要先得到容量为（j-weight[i]）时候的价值，即先得到 tab[i-1][j-weight[i]] ，所以 tab[i-1][j-weight[i]]+value[i] 为放入第i物品的价值； tab[i-1][j] 就是不放入第i个物品。

动态规划的思维就在这里体现了，即tab[i-1][j]是tab[i][j]的最优解（我觉得上面的思路讲解较容易理解）。

例子：5个物品，（重量，价值）分别为：（5，12），（4，3），（7，10），（2，3），（6，6）。

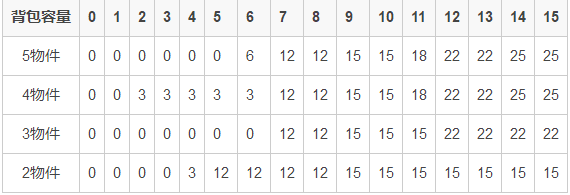
故有：

for i=[0,n)
    for(j=totle;j>=weight[i]; j--)
        tab[j] = max(tab[j-weight[i]]+value[i],tab[j])
 /* print tab[0][total] */


 完全背包


不死族的巫妖王发工资拉,死亡骑士拿到一张N元的钞票(记住,只有一张钞票),为了防止自己在战斗中频繁的死掉,他决定给自己买一些道具,于是他来到了地精商店前.


死亡骑士:"我要买道具!"


地精商人:"我们这里有三种道具,血瓶150块无限个,魔法药200块无限个,无敌药水350块无限个."


死亡骑士:"好的,给我一个血瓶."


说完他掏出那张N元的大钞递给地精商人.


地精商人:"我忘了提醒你了,我们这里没有找客人钱的习惯的,多的钱我们都当小费收了的,嘿嘿."


死亡骑士:"......你妹"


死亡骑士想,与其把钱当小费送个他还不如自己多买一点道具,反正以后都要买的,早点买了放在家里也好,但是要尽量少让他赚小费.


现在死亡骑士希望你能帮他计算一下,最少他要给地精商人多少小费.


上面的魔兽场景描述跟上面的只有小小的差异，就是物品有一个变为了无限个，这就是完全背包问题。完全背包问题可以描述为：


有n种物品，每种物品有无限个，每个物品的重量为weight[i]，每个物品的价值为value[i]。现在有一个背包，它所能容纳的重量为total，问：当你面对这么多有价值的物品时，你的背包所能带走的最大价值是多少？

有了上面01背包的式子，这题会变的容易理解很多，只是这个式子要有小小的改动。01背包在二维数组上操作，就是为了防止一个物品被放入多次的情况。因此一维数组可以满足完全背包的问题。如下：

tab[j] = max(tab[j-weight[i]]+value[i],tab[j]);({i,j|0<i<=n,0<=j<=total})

根本就是一样的，只不过物品可以被放多次。


故有：

for i=[0,n)
    for(j=weight[i]; j<=total; j++)
        tab[j] = max(tab[j-weight[i]]+value[i],tab[j])
/*    print tab[0][total]    */

 

 多重背包


不死族的巫妖王发工资拉,死亡骑士拿到一张N元的钞票(记住,只有一张钞票),为了防止自己在战斗中频繁的死掉,他决定给自己买一些道具,于是他来到了地精商店前.


死亡骑士:"我要买道具!"


地精商人:"我们这里有三种道具,血瓶150块a个,魔法药200块b个,无敌药水350块c个."


死亡骑士:"好的,给我一个血瓶."


说完他掏出那张N元的大钞递给地精商人.


地精商人:"我忘了提醒你了,我们这里没有找客人钱的习惯的,多的钱我们都当小费收了的,嘿嘿."


死亡骑士:"......你妹"


死亡骑士想,与其把钱当小费送个他还不如自己多买一点道具,反正以后都要买的,早点买了放在家里也好,但是要尽量少让他赚小费.


现在死亡骑士希望你能帮他计算一下,最少他要给地精商人多少小费.


上面的魔兽场景描述跟上面的又有了小小的差异，就是物品有一个变为了有限个，问题也就变成了多重背包问题。

 

有n种物品，每种物品有amount[i]个，每个物品的重量为weight[i]，每个物品的价值为value[i]。现在有一个背包，它所能容纳的重量为total，问：当你面对这么多有价值的物品时，你的背包所能带走的最大价值是多少？

多重和完全更接近，多了数量的限制，用一个count[n]计数数组来限制物品i的数量。当放入第i个物品是较优值的时候，count[i]=count[j-weight[i]]+1（j 的含义请查看代码）;这样做是因为，放入第i个物品的操作是基于count[j-weight[i]]放入的，所以当count[i-weight[i]]>=amount[i]时，就要阻止放入即便放入第i个物品是较优值。 故有：

for i=[0,n)
    /*    将count数组清零        */
    for(j=weight[i]; j<=total; j++)
        if    count[j-weight[i]]<amout[i]
            tab[j] = max(tab[j-weight[i]]+value[i],tab[j]);
            if    tab[j]=tab[j-weight[i]]+value[i]   //    决定放入i是较优解
                count[i] = count[j-weight[i]] + 1
        else    if    tab[j]=0       //    防止装第1个物品和装其他物品的情况
            tab[j] = tab[j-1],count[j] = count[j-1]
        else    count[j] = count[j-1]
/*    print tab[0][total]    */

 相关例题

HDU2546：饭卡
http://acm.hdu.edu.cn/showproblem.php?pid=2546(01背包)
要注意的是这里只要剩余的钱不低于5元，就可以购买任何一件物品，所以5在这道题中是很特许的，

再使用01背包之前，我们首先要在现在所拥有的余额中保留5元，用这五元去购买最贵的物品，

而剩下的钱就是背包的总容量，可以随意使用

#include <stdio.h>
#include <algorithm>
using namespace std;
int main()
{
    int n;
    while(~scanf("%d",&n),n)
    {
        int i,price[2013]= {0},dp[2013] = {0};
        for(i = 1; i<=n; i++)
            scanf("%d",&price[i]);
        sort(price+1,price+1+n);
        int MAX=price[n];
        int j,m;
        scanf("%d",&m);
        if(m<5)//低于5元不能购买
        {
            printf("%d\n",m);
            continue;
        }
        m-=5;//取出5元用于购买最贵的物品
        for(i = 1; i<n; i++)//01背包
        {
            for(j = m;j>=price[i];j--)
            {
                dp[j] = max(dp[j],dp[j-price[i]]+price[i]);
            }
        }
        printf("%d\n",m+5-dp[m]-MAX);
    }
    return 0;
}

 

HDU 4508湫湫系列故事——减肥记I

http://acm.hdu.edu.cn/showproblem.php?pid=4508(完全背包)

#include<iostream>
#include<algorithm>
using namespace std;
int max(int a,int b)
{
	if(a>b) return a;
    else    return b;
}
int main()
{
	int n,m;
	int a[100005],b[100005],c[100005];
	while(scanf("%d",&n)!=EOF)
	{
		memset(c,0,sizeof(c));
		for(int i=0;i<n;i++)
			scanf("%d%d",&a[i],&b[i]);
		scanf("%d",&m);
		for(int j=0;j<n;j++)
		{
			for(int k=b[j];k<=m;k++)
			{
				c[k]=max(c[k-b[j]]+a[j],c[k]);
			}
		}
		printf("%d\n",c[m]);
	}
	return 0;
}

 

hdu 2602 Bone Collector

http://acm.hdu.edu.cn/showproblem.php?pid=2602(01背包)

注意和上题进行比较。

#include<iostream>
#include<algorithm>
using namespace std;
int max(int a,int b)
{
	if(a>b) return a;
    else    return b;
}
int main()
{
	int T,N,V;
	int i,j,k;
	int v[1005],w[1005],c[1005];
	scanf("%d",&T);
	while(T--)
	{
		scanf("%d%d",&N,&V);
		for(i=0;i<N;i++)
			scanf("%d",&v[i]);
		for(i=0;i<N;i++)
			scanf("%d",&w[i]);
		memset(c,0,sizeof(c));
		for(i=0;i<N;i++)
		{
			for(j=V;j>=w[i];j--)
			{
				c[j]=max(c[j],c[j-w[i]]+v[i]);
			}
		}
		printf("%d\n",c[V]);
	}
	return 0;
}

相关链接点击打开链接
 

HDU 1203I NEED A OFFER!

#include <iostream>
#include<algorithm>
using namespace std;
const int N=10000+1;
int a[N];
float b[N],f[N]; 
int main(int argc, char *argv[])
{
    int n,m;
	while(scanf("%d%d",&n,&m)!=EOF&&m+n)
	{
		memset(f,0,sizeof(f));
		for(int i=0;i<m;i++) 
			cin>>a[i]>>b[i];
		for(int i=1;i<m;i++)
		{
			for(int j=n;j>a[i];j--)
			{
				f[j]=max(f[j],1-(1-f[j-a[i]])*(1-b[i]));
			}
		}
		printf("%.1f%%\n",f[n]*100); 
	} 
	return 0;
}
//01背包问题
问题大意：同学a要出国留学，他有n万元的存款，可以向m所学校申请，每所学校的费用c[i]，录取他的可能性w[i]，
根据n的数量，他可以同时向s所大学同时申请，假设共有q种申请方式，现在求q种方式中他被录取的最大的可能性是多少。
求前i所大学录取他的的最大可能性
假设他同时向两所学校申请，录取概率分别为a,b
他没被录取的概率是(1-a)*(1-b)
那么他被录取的概率是1-(1-a)*(1-b)
f[j] = max{f[j],1-(1-f[j-c[i]])*(1-w[i])}
max中的f[j]表示分析完上一所学校之后j万元能够获取的最大被录取概率
如果等号左边的f[j]等于max中的f[j]，就说明花费j万元时不向第i校申请，所以和第i-1校时的j万元所获取的最大被录取概率一样。
max中的(1-(1-f[j-c[i]])*(1-w[i]))表示选择了i校之后被录取的概率。
f[j-c[i]]:除去i校的申请费之后，用剩余的钱所获取的被录取最大概率。


HDU 1248寒冰王座

#include <stdio.h>
#include <string.h>
int max(int a,int b)
{
	return  a>b?a:b;
}
int main(int argc, char *argv[])
{
    int i,j,m,n;
	int dp[10001];
	int a[3]={150,200,350};
	scanf("%d",&n);
	while(n--)
	{
		scanf("%d",&m);
		memset(dp,0,sizeof(dp));
		for(i=0;i<3;i++)
		{
			for(j=a[i];j<=m;j++)
			{
				dp[j]=max(dp[j],dp[j-a[i]]+a[i]);
			}    
		}
		printf("%d\n",m-dp[m]);
	}   
	return 0;
}
//完全背包问题


HDU 2602 Bone Collector

#include <iostream>
#include <cstring>
using namespace std;
int dp[1001], v[1000], p[1000];
inline int max(int a, int b) { return a>b?a:b;  }
int main()
{ int c;
scanf("%d", &c);
while (c--) {
	int n, V, i, j;
	scanf("%d %d", &n, &V);
	for (i=0; i<n; i++)   
		scanf("%d", &p[i]);
	for (i=0; i<n; i++)  
		scanf("%d", &v[i]);
	memset(dp, 0, sizeof(dp));
	for (i=0; i<n; i++)
		for (j=V; j>=v[i]; j--)
			dp[j] = max(dp[j], dp[j-v[i]] + p[i]);
		printf("%d\n", dp[V]);
}
}
//01背包问题

 

首先我们把三种情况放在一起来看：

01背包（ZeroOnePack）: 有N件物品和一个容量为V的背包。（每种物品均只有一件）第i件物品的费用是c[i]，价值是w[i]。求解将哪些物品装入背包可使价值总和最大。

完全背包(CompletePack): 有N种物品和一个容量为V的背包，每种物品都有无限件可用。第i种物品的费用是c[i]，价值是w[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。

多重背包(MultiplePack): 有N种物品和一个容量为V的背包。第i种物品最多有n[i]件可用，每件费用是c[i]，价值是w[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。

比较三个题目，会发现不同点在于每种背包的数量，01背包是每种只有一件，完全背包是每种无限件，而多重背包是每种有限件。

——————————————————————————————————————————————————————————–：

01背包（ZeroOnePack）: 有N件物品和一个容量为V的背包。（每种物品均只有一件）第i件物品的费用是c[i]，价值是w[i]。求解将哪些物品装入背包可使价值总和最大。

这是最基础的背包问题，特点是：每种物品仅有一件，可以选择放或不放。

用子问题定义状态：即f[i][v]表示前i件物品恰放入一个容量为v的背包可以获得的最大价值。则其状态转移方程便是：

f[i][v]=max{f[i-1][v],f[i-1][v-c[i]]+w[i]}

把这个过程理解下：在前i件物品放进容量v的背包时，

它有两种情况：

第一种是第i件不放进去，这时所得价值为:f[i-1][v]

第二种是第i件放进去，这时所得价值为：f[i-1][v-c[i]]+w[i]

（第二种是什么意思？就是如果第i件放进去，那么在容量v-c[i]里就要放进前i-1件物品）

最后比较第一种与第二种所得价值的大小，哪种相对大，f[i][v]的值就是哪种。

（这是基础，要理解！）

这里是用二位数组存储的，可以把空间优化，用一位数组存储。

用f[0..v]表示，f[v]表示把前i件物品放入容量为v的背包里得到的价值。把i从1~n(n件)循环后，最后f[v]表示所求最大值。

*这里f[v]就相当于二位数组的f[i][v]。那么，如何得到f[i-1][v]和f[i-1][v-c[i]]+w[i]？（重点！思考）
首先要知道，我们是通过i从1到n的循环来依次表示前i件物品存入的状态。即：for i=1..N
现在思考如何能在是f[v]表示当前状态是容量为v的背包所得价值，而又使f[v]和f[v-c[i]]+w[i]标签前一状态的价值？

逆序！

这就是关键！

1for i=1..N
2   for v=V..0
3        f[v]=max{f[v],f[v-c[i]]+w[i]};
4

分析上面的代码：当内循环是逆序时，就可以保证后一个f[v]和f[v-c[i]]+w[i]是前一状态的！
这里给大家一组测试数据：

测试数据：
10,3
3,4
4,5
5,6

这个图表画得很好，借此来分析：

C[v]从物品i=1开始，循环到物品3，期间，每次逆序得到容量v在前i件物品时可以得到的最大值。（请在草稿纸上自己画一画）

这里以一道题目来具体看看：

题目：http://acm.hdu.edu.cn/showproblem.php?pid=2602

代码在这里：http://www.wutianqi.com/?p=533

分析：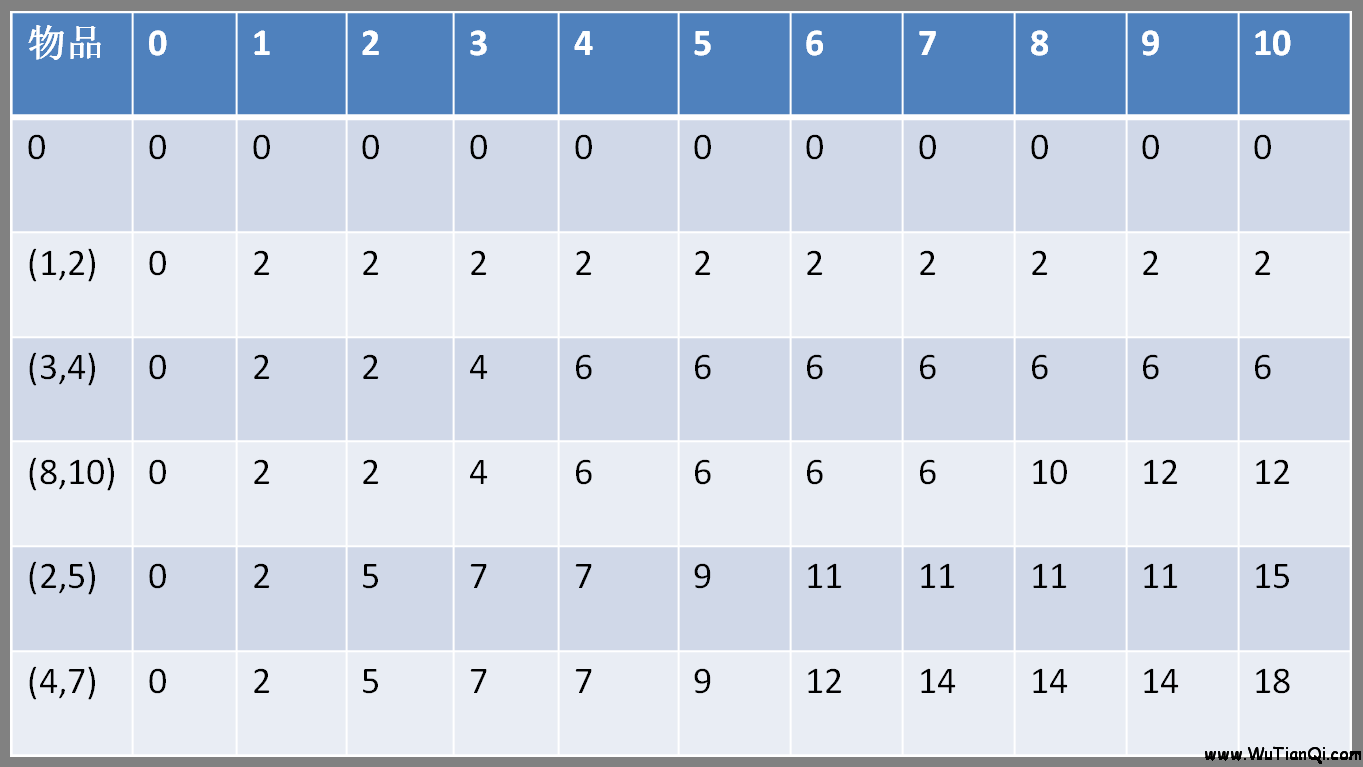

 

具体根据上面的解释以及我给出的代码分析。这题很基础，看懂上面的知识应该就会做了。

——————————————————————————————————————————————————————————–

完全背包：

完全背包(CompletePack): 有N种物品和一个容量为V的背包，每种物品都有无限件可用。第i种物品的费用是c[i]，价值是w[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。

完全背包按其思路仍然可以用一个二维数组来写出：

f[i][v]=max{f[i-1][v-k*c[i]]+k*w[i]|0<=k*c[i]<=v}

同样可以转换成一维数组来表示：

伪代码如下：
 

for i=1..N
    for v=0..V
        f[v]=max{f[v],f[v-c[i]]+w[i]}


 

顺序！

想必大家看出了和01背包的区别，这里的内循环是顺序的，而01背包是逆序的。
现在关键的是考虑：为何完全背包可以这么写？
在次我们先来回忆下，01背包逆序的原因？是为了是max中的两项是前一状态值，这就对了。
那么这里，我们顺序写，这里的max中的两项当然就是当前状态的值了，为何？
因为每种背包都是无限的。当我们把i从1到N循环时，f[v]表示容量为v在前i种背包时所得的价值，这里我们要添加的不是前一个背包，而是当前背包。所以我们要考虑的当然是当前状态。
这里同样给大家一道题目：

题目：http://acm.hdu.edu.cn/showproblem.php?pid=1114

代码：http://www.wutianqi.com/?p=535

（分析代码也是学习算法的一种途径，有时并不一定要看算法分析，结合题目反而更容易理解。）

——————————————————————————————————————————————————————————–

多重背包

多重背包(MultiplePack): 有N种物品和一个容量为V的背包。第i种物品最多有n[i]件可用，每件费用是c[i]，价值是w[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。

这题目和完全背包问题很类似。基本的方程只需将完全背包问题的方程略微一改即可，因为对于第i种物品有n[i]+1种策略：取0件，取1件……取n[i]件。令f[i][v]表示前i种物品恰放入一个容量为v的背包的最大权值，则有状态转移方程：

f[i][v]=max{f[i-1][v-k*c[i]]+k*w[i]|0<=k<=n[i]}

这里同样转换为01背包：

普通的转换对于数量较多时，则可能会超时，可以转换成二进制（暂时不了解，所以先不讲）

对于普通的。就是多了一个中间的循环，把j=0~bag[i]，表示把第i中背包从取0件枚举到取bag[i]件。

给出一个例题：

题目：http://acm.hdu.edu.cn/showproblem.php?pid=2191

代码：http://www.wutianqi.com/?p=537

 

 

 

 

转载于:https://my.oschina.net/lin546/blog/1619880

ACM解题心得
qq_43239615的博客
03-24 359
不死族的巫妖王发工资拉,死亡骑士拿到一张N元的钞票(记住,只有一张钞票),为了防止自己在战斗中频繁的死掉,他决定给自己买一些道具,于是他来到了地精商店前. 死亡骑士:“我要买道具!” 地精商人:“我们这里有三种道具,血瓶150块一个,魔法药200块一个,无敌药水350块一个.” 死亡骑士:“好的,给我一个血瓶.” 说完他掏出那张N元的大钞递给地精商人. 地精商人:“我忘了提醒你了,我们这里没有找客...
Leetcode 背包问题汇总
No_Game_No_Life_的博客
06-10 2282
文章目录背包月背包：大小与数量 背包月 本月是背包月，接连出了好几个背包问题，其难点在于对于问题的建模和分析。 比如下面两道题： 474. 一和零 494. 目标和 这两道题的不同点在于： 前者是求大小，而后者是求数量。 又比如下面这道题： 1049. 最后一块石头的重量 II 它的解法实际上就是一个典型的求大小的01背包问题——容量有限情况下的问题，而难点在于“建模”。 ttodo 硬币 又比如背包问题的变种： 1449.数位成本和为目标值的最大数字 这是无限可拿的完全背包问题，容量有限而可装
寒冰王座
dianminba7855的博客
12-19 253
题目描述： 不死族的巫妖王发工资拉,死亡骑士拿到一张N元的钞票(记住,只有一张钞票),为了防止自己在战斗中频繁的死掉,他决定给自己买一些道具,于是他来到了地精商店前. 死亡骑士:"我要买道具!" 地精商人:"我们这里有三种道具,血瓶150块一个,魔法药200块一个,无敌药水350块一个." 死亡骑士:"好的,给我一个血瓶." 说完他掏出那张N元的大钞递给地精商人. 地精商人:...
每日一练
Shrimp_millet
07-02 532
题目描述： 不死族的巫妖王一般会在月末给死亡骑士发工资，而死亡骑士拿到工资（总是为一张N元的钞票，记住，只有一张钞票），为了防止下月自己在战斗中频繁的死掉，他会给自己买一些道具，于是他来到了地精商店前 死亡骑士：“我要买道具！” 地精商人：“我们这里有三种道具，血瓶150块一个，魔法药200块一个，无敌药水350块一个。” 死亡骑士：“好的，给我一个血瓶” 说完他掏出那张N元的大钞递给地...
2021-02-02 背包入门
m0_52380041的博客
02-03 288
背包 01背包 A - Bone Collector Many years ago , in Teddy’s hometown there was a man who was called “Bone Collector”. This man like to collect varies of bones , such as dog’s , cow’s , also he went to the grave … The bone collector had a big bag with a volume o
背包问题.rar_matlab算法实现背包问题_价值背包算法_背包最大价值_背包问题_遗传算法 背包
07-15
总结，本项目通过MATLAB实现了遗传算法对背包问题的求解，尤其针对价值背包问题，达到了较好的效果。这种实现方式对于理解和应用遗传算法解决实际问题具有重要的参考价值，同时展示了MATLAB在优化问题上的强大功能。
【leetcode】动态规划刷题总结（三）-背包问题
最新发布
zs16113的博客
05-12 467
有n件物品和一个最多能背重量为w的背包。第i件物品的重量是weight[i]，得到的价值是value[i]。01背包是每件物品只能用一次；完全背包是每件物品数量无限。求解目标是将哪些物品装入背包里物品价值总和最大。
动态规划-死亡骑士
No Pain, No Gain .
03-26 381
题目： 不死族的巫妖王发工资拉,死亡骑士拿到一张N元的钞票(记住,只有一张钞票),为了防止自己在战斗中频繁的死掉,他决定给自己买一些道具,于是他来到了地精商店前. 死亡骑士:“我要买道具!” 地精商人:“我们这里有三种道具,血瓶150块一个,魔法药200块一个,无敌药水350块一个.” 死亡骑士:“好的,给我一个血瓶.” 说完他掏出那张N元的大钞递给地精商人. 地精商人:“我忘了提醒你了,我们这里...
字节跳动笔试题（三）——寒冰王座
不积跬步无以至千里
07-16 6636
字节笔试题（三）
模板——完全背包
Ember_Sky
05-06 187
完全背包 Problem Description 不死族的巫妖王发工资拉,死亡骑士拿到一张N元的钞票(记住,只有一张钞票),为了防止自己在战斗中频繁的死掉,他决定给自己买一些道具,于是他来到了地精商店前. 死亡骑士:“我要买道具!” 地精商人:“我们这里有三种道具,血瓶150块一个,魔法药200块一个,无敌药水350块一个.” 死亡骑士:“好的,给我一个血瓶. 说完他掏出那张N元的大钞递给地精商人...
HDU 1248 寒冰王座
weixin_33737774的博客
09-22 4443
HDU 1248 寒冰王座 题干 Problem Description 不死族的巫妖王发工资拉,死亡骑士拿到一张N元的钞票(记住,只有一张钞票),为了防止自己在战斗中频繁的死掉,他决定给自己买一些道具,于是他来到了地精商店前. 死亡骑士:”我要买道具!” 地精商人:”我们这里有三种道具,血瓶150块一个,魔法药200块一个,无敌药水350块一个...
3月18 周作业题解
weixin_34068198的博客
03-18 357
寒冰王座 Time Limit : 2000/1000ms (Java/Other)Memory Limit : 65536/32768K (Java/Other) Total Submission(s) : 38Accepted Submission(s) : 18 Font: Times New Roman | Verdana | Georgia Font Size: ← ...
HDU 1248 寒冰王座 (完全背包)
二十五之前我可能会秃头
05-24 544
Description 不死族的巫妖王发工资拉,死亡骑士拿到一张N元的钞票(记住,只有一张钞票),为了防止自己在战斗中频繁的死掉,他决定给自己买一些道具,于是他来到了地精商店前.  死亡骑士:"我要买道具!"  地精商人:"我们这里有三种道具,血瓶150块一个,魔法药200块一个,无敌药水350块一个."  死亡骑士:"好的,给我一个血瓶."  说完他掏出那张N元的大
杭电OJ 1248 完全背包问题 及反思
ssdut_209的博客
06-01 2078
Problem Description 不死族的巫妖王发工资拉,死亡骑士拿到一张N元的钞票(记住,只有一张钞票),为了防止自己在战斗中频繁的死掉,他决定给自己买一些道具,于是他来到了地精商店前. 死亡骑士:"我要买道具!" 地精商人:"我们这里有三种道具,血瓶150块一个,魔法药200块一个,无敌药水350块一个." 死亡骑士:"好的,给我一个血瓶." 说完他掏出那张
头条面试题
HuaZi_Myth的博客
11-02 207
 待处理 极大似然的原理 SVM 原理 L1和L2的区别，以及各自的使用场景 为什么梯度是函数变化最快的方向 https://zhuanlan.zhihu.com/p/24913912 去除字符串连续字符 递归的去除字符串中连续的 ac 和 b #include <iostream> #include <vector> #include <st...
19 均分钱币(0 1背包问题)
weixin_41563161的博客
04-20 1200
均分钱币 题目大意： 给你一堆硬币，让你分成两堆，分别给A，B两个人，求两人得到的最小差。 解题思路： 求解两人分得钱币的最小差值，巧妙地转化为01背包问题。 sum代表这堆钱币的总价值，ans=sum/2，求出得钱较少的人的钱币总量，即在这堆钱币中挑选出一定量的钱币，使得它的总值为小于...
0-1背包以及完全背包（如何输出包里的物件）
Fhang
04-02 3568
0-1 背包问题问题： 有Num个物品，每个物品的重量为weight[i]，每个物品的价值为value[i]。现在有一个背包，它所能容纳的重量为 M ，问：当你面对这么多有价值的物品时，你的背包所能带走的最大价值是多少？解决方法： 采用动态规划的方法解决。 01背包的状态转换方程 f[i,j] = Max{ f[i-1,j-Weight[i]]+Value[i] ( j >= Wi ), f
01背包问题实用测试数据汇总
01背包问题是计算机科学与运营研究中经典的组合优化问题。它属于动态规划的一个应用场景，解决的是在限定重量的前提下，如何选择物品以获得最大价值。该问题因其物品只能选择一件或不选择（即0-1选择）的特点而得名...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值