薛定谔-泊松方程多物理场接口可用于模拟包含诸如量子阱、量子线和量子点等载流子的量子约束系统。在本文中,我们将以砷化镓纳米线的基准模型为例,演示如何使用 COMSOL Multiphysics® 软件附加的“半导体模块”提供的这项功能。
薛定谔-泊松方程多物理场接口
自 COMSOL Multiphysics® 5.4 版本起,用户可以使用全新的薛定谔-泊松方程多物理场接口,在静电接口和薛定谔方程接口之间创建双向耦合,借此模拟量子约束系统中的载流子。“静电”的电势对薛定谔方程中的势能项有贡献。“薛定谔方程”特征态的概率密度的加权和对“静电”中的空间电荷密度有贡献。此接口支持所有空间维度,包括一维、一维轴对称、二维、二维轴对称以及三维。
求解薛定谔-泊松系统
薛定谔-泊松系统的特殊之处在于,静电分析需要稳态研究,而求解薛定谔方程需要特征值研究。为了求解双向耦合系统,我们对薛定谔方程和泊松方程进行迭代求解,直到获得自洽解。迭代过程包含以下步骤:
第 1 步
为了提供良好的初始迭代条件,求解泊松方程
(1)
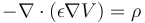
从而计算出电势
在这一初始化步骤中,
第 2 步
上一步获得的电势
(2)
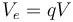
(3)
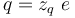
其中
第 3 步
利用基于 Eq. 2 推导出的新势能项,求解薛定谔方程,得到一组特征能量
第 4 步
利用概率密度的加权和,计算粒子密度分布
(4)
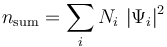
其中,权重
(5)








 本文详细介绍了COMSOL Multiphysics 5.4版本中新增的薛定谔-泊松方程多物理场接口,用于模拟量子约束系统,如量子阱、量子线和量子点。通过示例展示如何解决薛定谔-泊松系统,包括迭代求解过程和基准模型——砷化镓纳米线的模拟,最终得到自洽解。
本文详细介绍了COMSOL Multiphysics 5.4版本中新增的薛定谔-泊松方程多物理场接口,用于模拟量子约束系统,如量子阱、量子线和量子点。通过示例展示如何解决薛定谔-泊松系统,包括迭代求解过程和基准模型——砷化镓纳米线的模拟,最终得到自洽解。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章
















 1464
1464

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








