微积分13--泰勒公式

2019独角兽企业重金招聘Python工程师标准>>>

总结

1.sinx~x,tanx~x

2.(tanx)'=sec^2x

3.[(secx)^2] '
=2secx·(secx) '
=2secx·secx·tanx
=2(secx)^2·tanx

4.洛必达法则，要注意函数趋近于某个值的两个极限值都是为0的，且两个函数的导数比值是存在

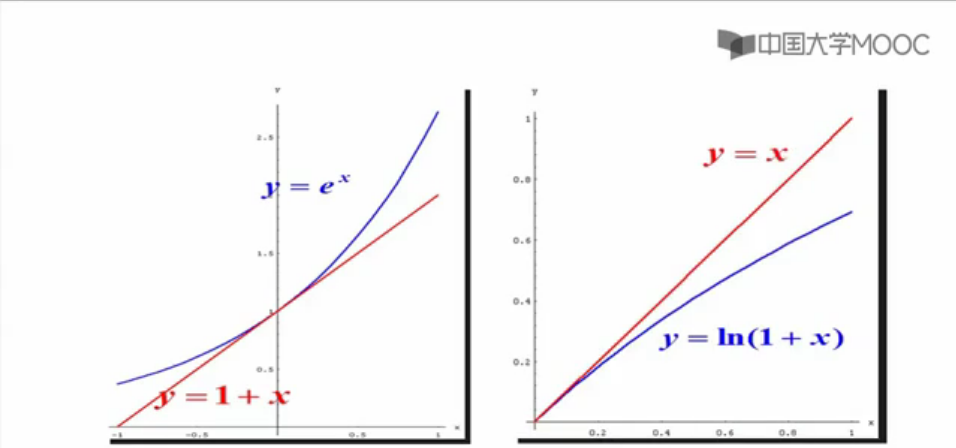
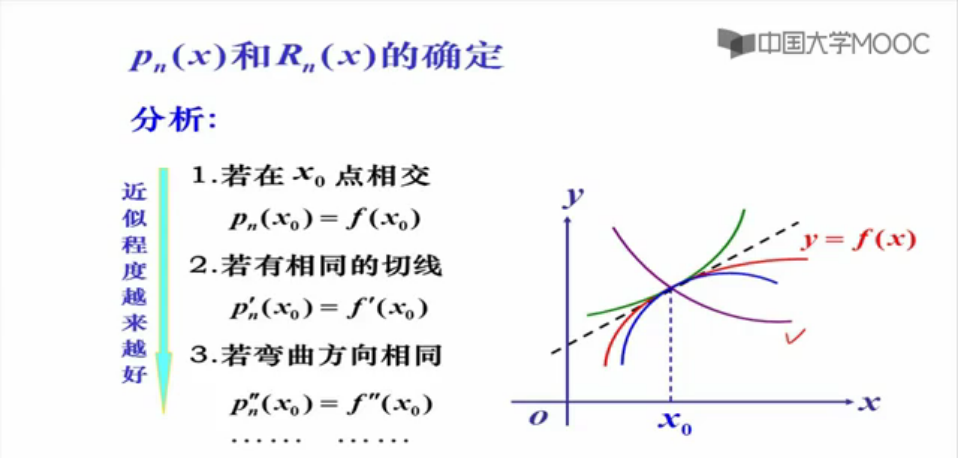
以上是过程，下面是结论

麦克劳林

例

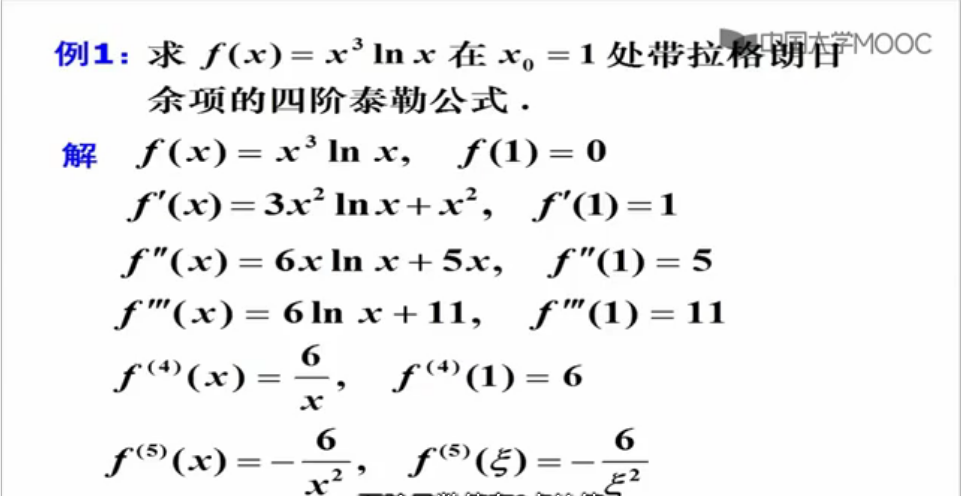
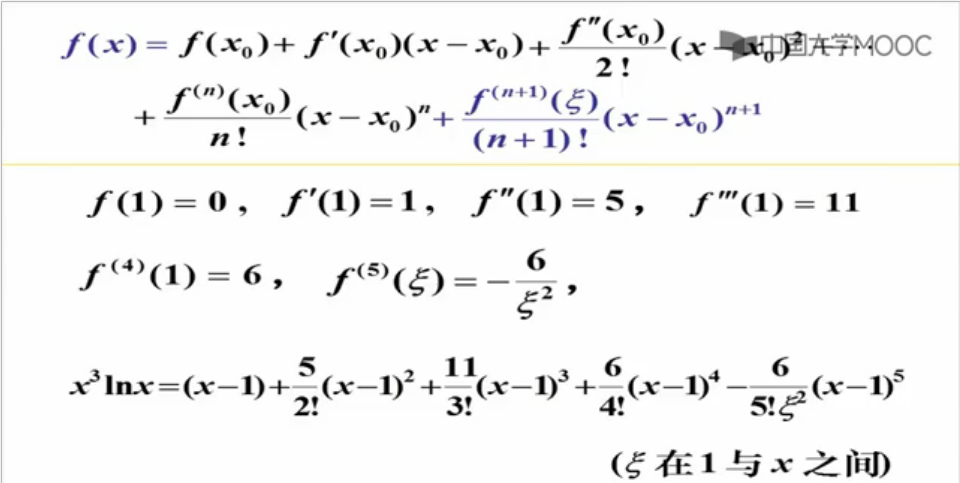
应用

y＝sinX的五阶导数求法

y=sinx
y^(1)=y'=cosx
y^(2)=y''=-sinx
y^(3)=y'''=-cosx
y^(4)=y''''=sinx
……
 
设n=4k+m，其中k∈N，m=0,1,2,3
则y^(n)=y^(m)=
{　sinx，m=0
{　cosx，m=1
{　-sinx，m=2
{　-cosx，m=3
即(sinx)^(n)=sin(x+nπ/2)
 
故(sinx)^(5)=sin(x+5π/2)=sin(x+π/2)=cosx

直接套用麦克劳林公式，其中m,n均为次数。佩亚诺余项的指数代数表达式不同，所以最后的指数有差异。

方法一

方法二

加减之间慎用等价无穷小

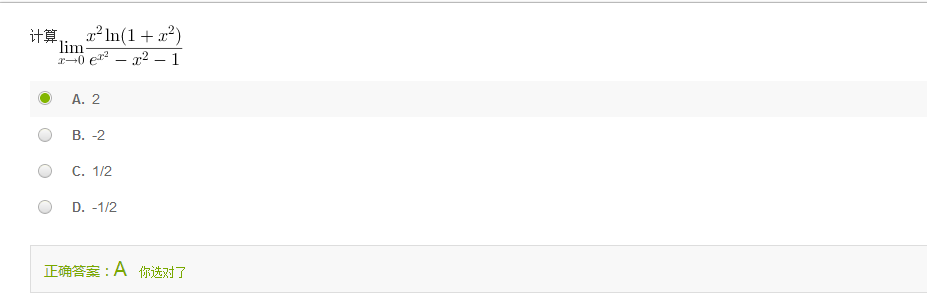
方法一通过这题学会使用“假设”，同时，最后通过等价无穷小找到答案。

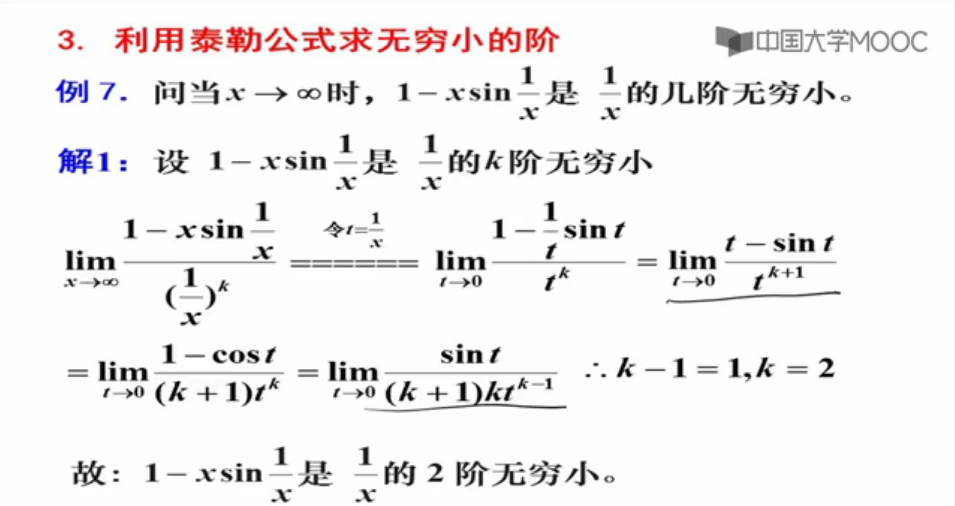
方法二

注意：最后一行使用公式来求4阶导数值，熟练使用公式

麦克劳林展开式太繁琐了

 

再来一次公式大总结，做到熟练运用

 

转载于:https://my.oschina.net/Bettyty/blog/794076