坐标系与参数方程的考向整理【三轮总结】

一、考向总结

• A、借助三角函数知识考察，比如利用三角函数求最值；
  

• B、借助直线的参数方程的参数\(t\)的几何意义考察，比如求线段的长度；
  

• C、借助平面几何知识考察，比如求倾斜角等；
  

• D、借助极坐标考查面积，线段长度等，
  

• E、借助解析几何考查，比如相关点法求轨迹，
  

• F、借助极坐标直接思考运算，不再转化到直角坐标系下思考；
  

• G、相关弦长公式：

\(|AB|\xlongequal[韦达定理]{直角坐标系下}\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}=|x_1-x_2|\cdot \sqrt{1+k^2}\)

\(= \sqrt{(x_1+x_2)^2-4x_1x_2}\cdot \sqrt{1+k^2}\)

\(|AB|\xlongequal[极角相同]{极坐标系下}|\rho_1-\rho_2|\)

\(|AB|\xlongequal[参数的几何意义]{参数方程下}|t_1-t_2|\)

二、常见考查方向整理

1、考查伸缩变换

例01【伸缩变换】【2016洛阳模拟】
已知曲线$C$的极坐标方程是$\rho=2$，以极点为原点，极轴为$x$轴的正半轴建立平面直角坐标系，直线$l$的参数方程为 $\begin{cases}x=1+t\\y=2+\sqrt{3}t\end{cases}(t为参数)$， （1）写出直线$l$的普通方程与曲线$C$的直角坐标方程； （2）设曲线$C$经过伸缩变换$\begin{cases}x'=x\\y'=\cfrac{1}{2}y\end{cases}$得到曲线$C'$， 设$M(x，y)$为曲线$C'$上任意一点，求$x^2-\sqrt{3}xy+2y^2$的最小值，并求相应的点$M$的坐标。 分析：(1)消去参数$t$，得到直线$l$的普通方程为$\sqrt{3}x-y-\sqrt{3}+2=0$ 由$\rho=2$，得到曲线$C$的直角坐标方程为$x^2+y^2=4$； (2)曲线$C：x^2+y^2=4$经过伸缩变换$\begin{cases}x'=x\\y'=\cfrac{1}{2}y\end{cases}$得到曲线$C'$， 即将$x=x'，y=2y'$代入$C：x^2+y^2=4$得到，$x'^2+4y'^2=4$， 整理得到曲线$C'：\cfrac{x^2}{4}+y^2=1$。 由曲线$C'$的参数方程得到点$M(2cos\theta，sin\theta)$， 即$x=2cos\theta，y=sin\theta$，代入得到 $x^2-\sqrt{3}xy+2y^2=(2cos\theta)^2-\sqrt{3}\cdot 2cos\theta\cdot sin\theta+2sin^2\theta$ $=4cos^2\theta+2sin^2\theta-\sqrt{3}sin2\theta$ $=2+2cos^2\theta-\sqrt{3}sin2\theta$ $=2+1+cos2\theta-\sqrt{3}sin2\theta$ $=3-2sin(2\theta-\cfrac{\pi}{6})$ 当$2\theta-\cfrac{\pi}{6}=2k\pi+\cfrac{\pi}{2}(k\in Z)$， 即$\theta=k\pi+\cfrac{\pi}{3}(k\in Z)$时， 即点$M(1，\cfrac{\sqrt{3}}{2})$或$M(-1，-\cfrac{\sqrt{3}}{2})$时， $x^2-\sqrt{3}xy+2y^2$的最小值为1.

2、参数方程与直角坐标方程的互化，极坐标方程与直角坐标方程的互化

例02(方程间的互化)
在直角坐标系$xOy$中，直线$l$是过定点$P(4，2)$且倾斜角为$\alpha$的直线；在极坐标系中，曲线$C$的极坐标方程为$\rho=4cos\theta$.
⑴写出直线$l$的参数方程，并将曲线$C$的极坐标方程化为直角坐标方程；
分析：直线$l$的参数方程为$\begin{cases} x=4+cos\alpha\cdot t \\ y=2+sin\alpha\cdot t \end{cases}(t为参数)$，
曲线$C$的直角坐标方程为$x^2+y^2=4x$；
(2016全国卷Ⅱ第23题高考真题)在直角坐标系$xOy$中，圆$C$ 的方程为$(x+6)^2+y^2=25$．
(1)以坐标原点为极点，$x$轴的正半轴为极轴建立极坐标系，求$C$的极坐标方程。
分析：由于极坐标方程中只有$\rho$和$\theta$，
故只要将$x=\rho\cdot cos\theta$和$y=\rho\cdot sin\theta$代入圆$C$的直角坐标方程为$(x+6)^2+y^2=25$，
整理可得$\rho^2+12\rho cos\theta+11=0$。
解后反思：
1、消参的方法有代入消参，加减消参，乘除消参，和平方消参等
乘除消参，比如$\begin{cases}x=t cos\theta\\y=t sin\theta\end{cases}(t为参数)$ ，两式相除得到$y=tan\theta x$，
再比如$\begin{cases}y=k(x-2)\\y=\cfrac{1}{k}(x+2)\end{cases}(k为参数)$
两式相乘，消去参数$k$，得到$y^2=x^2-4$，
2、直角坐标方程与极坐标方程的转化公式。

3、利用直线的参数方程几何意义求弦长

例03
在直角坐标系$xOy$中，直线$l$的参数方程为$\begin{cases} x=3-\cfrac{\sqrt{2}}{2}\cdot t \\ y=\sqrt{5}+\cfrac{\sqrt{2}}{2}\cdot t \end{cases}(t为参数)$，在极坐标系中圆$C$的方程为$\rho=2\sqrt{5}sin\theta$.
⑴求圆的直角坐标方程；
⑵设圆$C$与直线$l$交于点$A、B$，若点$P$的坐标为$(3，\sqrt{5})$，求$|PA|+|PB|$.
分析： ⑴简解，$x^2+(y-\sqrt{5})^2=5$
⑵思路一：将直线和圆的直角坐标方程联立，
求得交点$A、B$的坐标，
能否用两点间的坐标公式求解$|PA|+|PB|$.
思路二：利用直线参数方程的参数的几何意义，
将直线的参数方程$\begin{cases} x=3-\cfrac{\sqrt{2}}{2}\cdot t \\ y=\sqrt{5}+\cfrac{\sqrt{2}}{2}\cdot t \end{cases}(t为参数)$
代入圆的直角坐标方程，
得到$(3-\cfrac{\sqrt{2}}{2}\cdot t)^2+(\sqrt{5}+\cfrac{\sqrt{2}}{2}\cdot t -\sqrt{5})^2=5$
整理为$t^2-3\sqrt{2}t+4=0$，
由于$\Delta >0$，故可设点$A、B$分别对应参数$t_1，t_2$，
则$\begin{cases} t_1+ t_2=3\sqrt{2} \\ t_1\times t_2=4 \end{cases}$，
由此可以看出$t_1>0，t_2>0$，
故$|PA|=t_1，|PB|=t_2$，所以$|PA|+|PB|=3\sqrt{2}$.
解后反思：
1、这样的解法比利用两点间的距离公式的计算量要小得多。
2、求$|PA|\cdot |PB|=|t_1t_2|=t_1t_2=4$，务必注意两个根的正负，这与去绝对值符号有极大的关系。
3、求$|AB|=|t_1-t_2|$
4、求$\cfrac{1}{|PA|}+\cfrac{1}{|PB|}=\cfrac{|PA|+|PB|}{|PA||PB|}=\cfrac{t_1+t_2}{t_1t_2}$
5、若是出现了$t_1$和$t_2$中有一个负值的情形，如何求$|PA|+|PB|$呢？
不妨令$t_1<0$，$t_2>0$，则有$|PA|=|t_1|=-t_1$，$|PB|=|t_2|=t_2$，
那么$|PA|+|PB|=t_2-t_1=|t_2-t_1|$，
6、还可能会怎么考查呢？
比如已知$|PA|、|AB|、|PB|$成等比数列，这样$|AB|=|t_1-t_2|$，$|PA||PB|=|t_1t_2|$，且有$|AB|^2=|PA||PB|$，
比如已知$t_1+t_2=\cfrac{12\sqrt{3}}{13}$，$t_1t_2=-\cfrac{36}{13}$求$||PA|-|PB||$的值，
由$t_1t_2<0$，则可知$t_1、t_2$异号，那么可能$t_1<0，t_2>0$或者$t_1>0，t_2<0$，
则$||PA|-|PB||=|-t_1-t_2|=|t_1+t_2|=\cfrac{12\sqrt{3}}{13}$，或$||PA|-|PB||=|t_1-(-t_2)|=|t_1+t_2|=\cfrac{12\sqrt{3}}{13}$，

4、利用直线的参数方程几何意义求弦长的取值范围，

例04
在极坐标系中，已知圆$C$的圆心$C(\sqrt{2}，\cfrac{\pi}{4})$，半径$r=\sqrt{3}$，
（1）求圆$C$的极坐标方程。
（2）若$\alpha \in[0,\cfrac{\pi}{4}]$，直线$l$的参数方程为$\begin{cases} x=2+cos\alpha\cdot t \\ y=2+sin\alpha\cdot t \end{cases}(t为参数)$，
直线$l$交圆$C$于$A、B$两点，求弦长$|AB|$的取值范围。
解：（1）圆$C$的圆心$C(\sqrt{2}，\cfrac{\pi}{4})$，
得$C$的直角坐标为$(1,1)$，
所以圆$C$的直角坐标方程为$(x-1)^2+(y-1)^2=3$，
由$x=\rho cos\theta,y=\rho sin\theta$得到，
圆$C$的极坐标方程为$\rho^2-2\rho cos\theta-2\rho sin\theta-1=0$。

（2）将 $\begin{cases} x=2+cos\alpha\cdot t \\y=2+sin\alpha\cdot t \end{cases}(t为参数)$，
代入圆$C$的直角坐标方程为$(x-1)^2+(y-1)^2=3$，
得到$t^2+2(cos\alpha+sin\alpha)t-1=0$，
则有$\Delta= 4(cos\alpha+sin\alpha)^2+4>0$，
设$A、B$两点对应的参数分别为$t_1，t_2$，
则由韦达定理可知，
$t_1+t_2=2(cos\alpha+sin\alpha)，t_1\cdot t_2= -1$
所以弦长$|AB|=|t_1-t_2|=\sqrt{(t_1+t_2)^2-4t_1t_2}=\sqrt{8+4sin2\alpha}$，
由于$\alpha \in[0,\cfrac{\pi}{4}]$， 所以$sin2\alpha\in[0，1]$，$8+4sin2\alpha\in[8，12]$，
所以弦长$|AB|\in[2\sqrt{2}，2\sqrt{3}]$。

5、求曲线上的点到直线的距离的最值

例05【自编】
给定椭圆$\cfrac{x^2}{3}+y^2=1$和直线$x+y-8=0$，已知点P是椭圆上的一个动点，求点P到直线的距离的最小值。
分析：首先易知椭圆和直线没有交点，即二者相离，从而可以考虑用椭圆的参数方程或平行线法求解。
法1、利用椭圆的参数方程，由椭圆方程$\cfrac{x^2}{3}+y^2=1$可知，
动点坐标$P(\sqrt{3}cos\theta，sin\theta)$，
则点P到直线$x+y-8=0$的距离
$d(\theta)=\cfrac{|\sqrt{3}cos\theta+sin\theta-8|}{\sqrt{2}}=\cfrac{|2sin(\theta+\cfrac{\pi}{3})-8|}{\sqrt{2}}$，
故当$sin(\theta+\cfrac{\pi}{3})=1$时，$d_{min}=\cfrac{|2-8|}{\sqrt{2}}=3\sqrt{2}$；
$sin(\theta+\cfrac{\pi}{3})=-1$时，$d_{max}=\cfrac{|-2-8|}{\sqrt{2}}=5\sqrt{2}$；
【问题】为什么不设点P的坐标为$(x，y)$而采用参数坐标形式$(\sqrt{3}cos\theta，sin\theta)$?
前者坐标形式是二元形式，后者是一元形式，故后者简单。
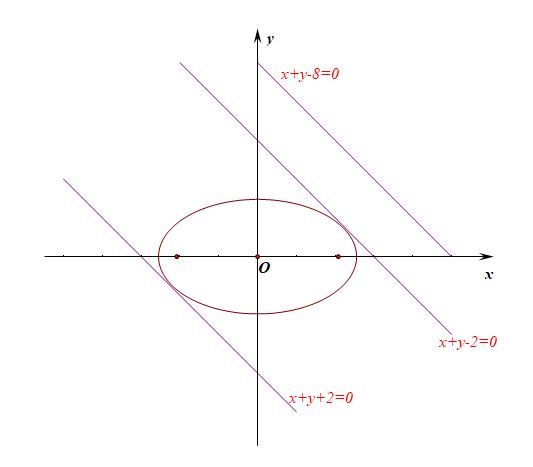法2、平行线法，设和已知平行且和已知椭圆相切的直线$x+y+m=0$，
则由$x+y+m=0$和$\cfrac{x^2}{3}+y^2=1$，消去$y$可得$4x^2+6mx+3m^2-3=0$，
由二者相切可知，$\Delta=36m^2-4\times4(3m^2-3)=0$，解得$m=\pm 2$，
即和椭圆相切的直线有$x+y-2=0$和$x+y+2=0$，故切点到直线$x+y-8=0$的距离就可以用两条平行线间的距离来刻画，
则$d_{max}=\cfrac{|2-(-8)|}{\sqrt{2}}=5\sqrt{2}$，$d_{min}=\cfrac{|-2-(-8)|}{\sqrt{2}}=3\sqrt{2}$。
【反思总结】1、如果将椭圆换成圆，再求圆上的动点到直线的距离的最值，可以考虑的方法有：
其一，圆的参数方程法；其二，平行线法；其三，几何法，圆心到直线的距离加减半径。
例05-2【2017$\cdot$江苏卷】
在平面直角坐标系$xoy$中，已知直线$l$的参数方程是$\begin{cases}x=-8+t\\y=\cfrac{t}{2}\end{cases}(t为参数)$，
曲线$C$的参数方程是$\begin{cases}x=2s^2\\y=2\sqrt{2}s\end{cases}(s为参数)$，设$P$为曲线$C$上的动点，
求点$P$到直线$l$的距离的最小值。
分析：直线$l$的直角坐标方程是$x-2y+8=0$，曲线$C$上的动点$P$的坐标$(2s^2，2\sqrt{2}s)$，
则由点到直线的距离公式可得，
$d=d(s)=\cfrac{|2s^2-4\sqrt{2}s+8|}{\sqrt{1^2+(-2)^2}}$
$=\cfrac{|2(s-\sqrt{2})^2+4|}{\sqrt{5}}$
当$s=\sqrt{2}$时，$d_{min}=\cfrac{4\sqrt{5}}{5}$。
解后反思：
1、利用抛物线的参数方程和点线距公式转化为二次函数的最值问题。
2、本题目还可以利用平行线法来求解。

6、求周长的最值

例06
在极坐标系中，曲线$C$的极坐标方程为$\rho^2=\cfrac{3}{1+2sin^2\theta}$和点$R(2\sqrt{2}，\cfrac{\pi}{4})$
⑴将曲线$C$的极坐标方程化为直角坐标方程；
⑵设点$P$为曲线$C$上一动点，矩形$PQRS$以$PR$为其对角线，且矩形的一边垂直于极轴，求矩形$PQRS$的周长的最小值及此时点$P$的直角坐标。
分析：⑴将曲线$C$的极坐标方程为$\rho^2=\cfrac{3}{1+2sin^2\theta}$变形为$\rho^2+2(\rho sin\theta)^2=3$，
即$x^2+y^2+2y^2=x^2+3y^2=3$，也就是$\cfrac{x^2}{3}+y^2=1$；
⑵作出大致图像， 课件地址
我们可以作出点$P$的坐标$P(\sqrt{3}cos\theta，sin\theta)$，
那么点$Q(2，sin\theta)$，点$R(2，2)$，则$|PQ|=2-\sqrt{3}cos\theta$，$|RQ|=2-sin\theta$，
则$|PQ|+|RQ|=4-2sin(\theta+\cfrac{\pi}{3})$，
当$\theta=\cfrac{\pi}{6}$时，$(|PQ|+|RQ|)_{min}=2$，所以矩形$PQRS$的周长的最小值为4，
此时点$P$的坐标为$(\sqrt{3}cos\cfrac{\pi}{6}，sin\cfrac{\pi}{6})$，即$(\cfrac{3}{2}，\cfrac{1}{2})$。

7、求面积的最值

例7【2018宝鸡市二检文理科第22题】
在直角坐标系$xoy$中，曲线$C_1$的参数方程为$\begin{cases}x=2+2cos\alpha\\y=2sin\alpha\end{cases}(\alpha为参数)$，
以坐标原点为极点，以$x$轴正半轴为极轴，建立极坐标系，曲线$C_2$的极坐标方程为$\rho=2cos\theta$。
(1)写出曲线$C_1$的普通方程和$C_2$的直角坐标方程；
(2)设点$P$ 在$C_1$上，点$Q$ 在$C_2$上，且$\angle POQ=\cfrac{\pi}{2}$，求三角形$POQ$面积的最大值。
分析：(1) 直接给出答案，
曲线的普通方程$C_1：(x-2)^2+y^2=4$；
所求的直角坐标方程$C_2：(x-1)^2+y^2=1$；
(2)【法1】极坐标法(本题目命题意图就是想让学生体会极坐标的优越性，从而主动使用极坐标刻画思考或者在极坐标系下运算)，
曲线$C_1$的极坐标方程为$\rho_1=4cos\alpha(\alpha\in(-\cfrac{\pi}{2}，\cfrac{\pi}{2}))$，
曲线$C_2$的极坐标方程为$\rho_2=2cos\theta(\theta\in(-\cfrac{\pi}{2}，\cfrac{\pi}{2}))$，
如右图所示，初步分析，当点$P$在$x$轴上方时，点$Q$必在$x$轴下方；
当然还会有另一种情形，当点$P$在$x$轴下方时，点$Q$必在$x$轴上方；
我们取其中一种做研究，比如点$P$在$x$轴上方，点$Q$在$x$轴下方；
注意此时点$Q$的极角是负值$-\theta$，
由于$\rho_1>0$，$\rho_2>0$，以及$\angle POQ=\cfrac{\pi}{2}$可得，
$\alpha-\theta=\cfrac{\pi}{2}$，即$\alpha=\theta+\cfrac{\pi}{2}$，(顺时针为正，逆时针为负)
则有$S_{\Delta OPQ}=\cfrac{1}{2}|OP||OQ|$
$=\cfrac{1}{2}\rho_1\rho_2=\cfrac{1}{2}\times 4cos\alpha\times 2cos\theta$
$=4cos(\theta+\cfrac{\pi}{2})cos\theta=-4sin\theta cos\theta$
$=-2sin2\theta$，
当$2\theta=-\cfrac{\pi}{2}$，即$\theta=-\cfrac{\pi}{4}$时，
$(S_{\Delta OPQ})_{max}=2$。
【法2】参数方程法， 如图所示，曲线$C_1$的参数方程是$\begin{cases}x=2+2cos\alpha\\y=2sin\alpha\end{cases}(\alpha为参数，\alpha\in (-\pi，\pi))$，
曲线$C_2$的参数方程是$\begin{cases}x=1+cos\theta\\y=sin\theta\end{cases}(\theta为参数，\theta\in (-\pi，\pi))$，
注意参数的含义，$\cfrac{\alpha}{2}-\cfrac{\theta}{2}=\cfrac{\pi}{2}$，即$\alpha=\pi+\theta$
则有$S_{\Delta OPQ}=\cfrac{1}{2}|OP||OQ|$
$=\cfrac{1}{2}\sqrt{(2+2cos\alpha)^2+(2sin\alpha)^2}\sqrt{(1+cos\theta)^2+sin^2\theta}$
$=\cfrac{1}{2}\sqrt{8(1+cos\alpha)}\sqrt{2(1+cos\theta)}$
$=\cfrac{1}{2}\sqrt{8(1-cos\theta)}\sqrt{2(1+cos\theta)}$
$=\cfrac{1}{2}\times 4\sqrt{(1-cos\theta)(1+cos\theta)}$
$=2\sqrt{1-cos^2\theta}=2|sin\theta|$
当$\theta=-\cfrac{\pi}{2}$时，$(S_{\Delta OPQ})_{max}=2$。
【变形方法3】参数方程法，曲线$C_1$的参数方程是$\begin{cases}x=2+2cos\alpha\\y=2sin\alpha\end{cases}(\alpha为参数，\alpha\in (-\pi，\pi))$，
曲线$C_2$的参数方程是$\begin{cases}x=1+cos\theta\\y=2sin\theta\end{cases}(\theta为参数，\theta\in (-\pi，\pi))$，
注意参数的含义，$\cfrac{\alpha}{2}-\cfrac{\theta}{2}=\cfrac{\pi}{2}$，即$\alpha=\pi+\theta$
由$\angle POQ=\cfrac{\pi}{2}$可知，$k_{OP}k_{OQ}=-1$，
即$\cfrac{2sin\alpha}{2+2cos\alpha}\times \cfrac{sin\theta}{1+cos\theta}=-1$，即$-sin\alpha sin\theta=(1+cos\alpha)(1+cos\theta)$
$S_{\Delta OPQ}=\cfrac{1}{2}|OP||OQ|$
$=\cfrac{1}{2}\sqrt{(2+2cos\alpha)^2+(2sin\alpha)^2}\sqrt{(1+cos\theta)^2+sin^2\theta}$
$=\cfrac{1}{2}\sqrt{8(1+cos\alpha)}\sqrt{2(1+cos\theta)}$
$=2\sqrt{(1+cos\alpha)(1+cos\theta)}$
$=2\sqrt{-sin\alpha sin\theta}$，
又有$\cfrac{\alpha}{2}-\cfrac{\theta}{2}=\cfrac{\pi}{2}$，即$\alpha=\pi+\theta$
$原式=2\sqrt{sin^2\theta}=2|sin\theta|$，
当$\theta=-\cfrac{\pi}{2}$时，$(S_{\Delta OPQ})_{max}=2$。
【法4】尝试使用均值不等式，待有空思考整理。
设直线$OP$的方程为$y=kx$，由$\angle POQ=\cfrac{\pi}{2}$可得，
直线$OQ$的方程为$y=-\cfrac{1}{k}x$，
联立$\begin{cases}(x-2)^2+y^2=4\\y=kx\end{cases}$，
解得$P(\cfrac{4}{1+k^2}，\cfrac{4k}{1+k^2} )$，
联立$\begin{cases}(x-1)^2+y^2=1\\y=-\cfrac{1}{k}x\end{cases}$，
解得$ Q(\cfrac{2k^2}{1+k^2}，\cfrac{-2k}{1+k^2} )$，
$S_{\Delta POQ}=\cfrac{1}{2}|OP||OQ|=\cfrac{1}{2}\sqrt{(\cfrac{4}{1+k^2})^2+(\cfrac{4k}{1+k^2})^2}\sqrt{(\cfrac{2k^2}{1+k^2})^2+(\cfrac{-2k}{1+k^2})^2}$
$=\cfrac{1}{2}\sqrt{\cfrac{16}{1+k^2}}\sqrt{\cfrac{4k^2}{1+k^2}}=\cfrac{4|k|}{1+k^2}=\cfrac{4}{|k|+\frac{1}{|k|}}\leq 2$。
当且仅当$|k|=1$时取到等号。故$(S_{\Delta POQ})_{max}=2$。
反思：这个解法的优越性体现在只有一个变量$k$，那么求最值时就好操作些。
【法5】是否有，待后思考整理。
解后反思：
1、在高中数学中，求某个量(比如面积)的最值时，往往需要先表达出这个量(比如面积)的函数，这样求实际问题的最值就变成了求这个函数模型的最值问题了，这一过程实际就是函数的建模。
1、法1利用极坐标法，这样表达刻画面积时，就只有两个变量$\alpha$和$\theta$，然后利用两个变量的相互关系，再将变量集中为一个变量，就好求解其最大值了。
2、法2利用参数方程法，在表达刻画面积时，同样只有两个变量$\alpha$和$\theta$，然后利用两个变量的相互关系，再将变量集中为一个变量，就好求解其最大值了。法2和法3本质接近。
3、正确求解本题目，需要深刻理解极坐标方程的含义和参数方程的含义，尤其是法2对参数的含义更不能弄错了。用到了内外角关系和圆心角和圆周角关系。
4、还有学生想到设$P(x_1，y_1)$，$ Q(x_2，y_2)$，这样的思路我没有做尝试，不过能看出来此时是四个变量，这样就难得多了，所以碰到这样的题目我们先需要初步筛选思路。

8、求斜率或参数的值或取值范围

例08【2016全国卷Ⅱ第23题高考真题】
在直角坐标系$xOy$中，圆$C$ 的方程为$(x+6)^2+y^2=25$．
(1)以坐标原点为极点，$x$轴的正半轴为极轴建立极坐标系，求$C$的极坐标方程。
分析：由于极坐标方程中只有$\rho$和$\theta$，
故只要将$x=\rho\cdot cos\theta$和$y=\rho\cdot sin\theta$代入圆$C$的直角坐标方程为$(x+6)^2+y^2=25$，
整理可得$\rho^2+12\rho cos\theta+11=0$。
(2)直线$l$的参数方程为$\begin{cases} x=t\cdot cos\alpha \\ y=t\cdot sin\alpha \end{cases}(t为参数)$，
$l$与$C$交于A、B两点，$|AB|=\sqrt{10}$，求直线$l$的斜率。
【法1】参数方程法，
分析：本题目的求解要用到直线的参数方程的几何意义。
将直线$l$的参数方程代入圆$C$的直角坐标方程，
化简整理为$t^2+12t cos\alpha+11=0$，可设点$A、B$分别对应参数$t_1，t_2$，
则$\begin{cases} t_1+ t_2=-12cos\alpha \\ t_1\times t_2=11\end{cases}$，
$|AB|=|t_1-t_2|= \sqrt{(t_1+t_2)^2-4t_1t_2}=\sqrt{10}$，
解得$cos^2\alpha=\cfrac{54}{144}=\cfrac{3}{8}$，
又由图可知$\alpha\in [0，\pi)$，故$cos\alpha=\pm\cfrac{\sqrt{6}}{4}$，
则有$sin\alpha=\cfrac{\sqrt{10}}{4}$
故$tan\alpha=\cfrac{sin\alpha}{cos\alpha}=\cfrac{\cfrac{\sqrt{10}}{4} }{\pm\cfrac{\sqrt{6}}{4}} =\pm\cfrac{\sqrt{15}}{3}$。
故直线$l$的斜率为$\pm\cfrac{\sqrt{15}}{3}$。
【法2】极坐标系法，
圆$C$的极坐标方程是$\rho^2+12\rho cos\theta+11=0$。
将直线的参数方程两式相除得到，$y=tan\alpha x$，即$y=kx$，
则直线的极坐标方程为$\theta=\alpha(\rho\in R)$
将直线的极坐标方程代入圆$C$的极坐标方程是$\rho^2+12\rho cos\theta+11=0$，
得到圆$C$的极坐标方程是$\rho^2+12\rho cos\alpha+11=0$，
设点$A$的极坐标方程为$(\rho_1，\alpha)$，点$B$的极坐标方程为$(\rho_2，\alpha)$，
则$\rho_1+\rho_2=-12cos\alpha$，$\rho_1\cdot \rho_2=11$，
由$|AB|=|\rho_1-\rho_2|= \sqrt{(\rho_1+\rho_2)^2-4\rho_1\rho_2}=\sqrt{10}$，
解得$cos^2\alpha=\cfrac{54}{144}=\cfrac{3}{8}$，
又由图可知$\alpha\in [0，\pi)$，故$cos\alpha=\pm\cfrac{\sqrt{6}}{4}$，
则有$sin\alpha=\cfrac{\sqrt{10}}{4}$
故$tan\alpha=\cfrac{sin\alpha}{cos\alpha}=\cfrac{\cfrac{\sqrt{10}}{4} }{\pm\cfrac{\sqrt{6}}{4}} =\pm\cfrac{\sqrt{15}}{3}$。
故直线$l$的斜率为$\pm\cfrac{\sqrt{15}}{3}$。
【法3】平面几何法，
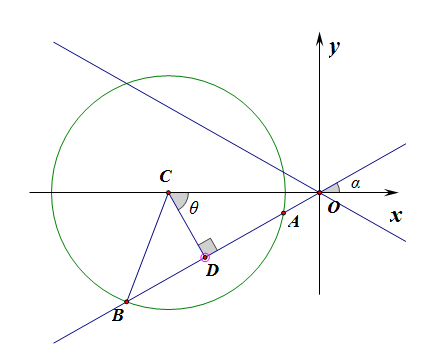如图所示，这样的直线应该有两条，且其斜率互为相反数，
现重点求解图中的直线$AB$的斜率，
在$Rt\Delta BCD$中，半径为$BC=5$，半弦长为$BD=\cfrac{\sqrt{10}}{2}$，
利用勾股定理求得，弦心距$CD=\cfrac{3\sqrt{10}}{2}$
在$Rt\Delta OCD$中，$OC=6$，$CD=\cfrac{3\sqrt{10}}{2}$
求得$cos\angle OCD=cos\theta=\cfrac{\sqrt{10}}{4}$
从而$sin\alpha=\cfrac{\sqrt{10}}{4}$，$cos\alpha=\cfrac{\sqrt{6}}{4}$，
即$k=tan\alpha=\cfrac{\sqrt{10}}{\sqrt{6}}=\cfrac{\sqrt{15}}{3}$，
故满足条件的直线$AB$有两条，其斜率为$\pm\cfrac{\sqrt{15}}{3}$。
例09【2017全国卷1，文科第22题高考真题】
在直角坐标系$xOy$中，曲线$C$ 的参数方程为$\begin{cases}x=3cos\theta\\y=sin\theta\end{cases}(\theta为参数)$，
直线$l$参数方程为$\begin{cases}x=a+4t\\y=1-t\end{cases}(t为参数)$，
(1)若$a=-1$，求$C$与$l$的交点坐标。
分析：将曲线$C$的参数方程转化为直角坐标方程为$\cfrac{x^2}{9}+y^2=1①$；
当$a=-1$时，将直线消掉参数得到$x+4y=3②$，
两式联立，解方程组得到 $\begin{cases}x=3\\y=0\end{cases}$
或$\begin{cases}x=-\cfrac{21}{25}\\y=\cfrac{24}{25}\end{cases}$，
故交点坐标为$(3，0)或(-\cfrac{21}{25}，\cfrac{24}{25})$。
(2)若$C$上的点到$l$的距离的最大值为$\sqrt{17}$，求$a$.
分析：曲线$C$上的任意一点$P(3cos\theta，sin\theta)$，
将直线$l$消掉参数得到$x+4y-4-a=0$，
则点P的直线$l$的距离为
$d=\cfrac{|3cos\theta+4sin\theta-4-a|}{\sqrt{17}}$
$=\cfrac{|5sin(\theta+\phi)-(4+a)|}{\sqrt{17}}(tan\phi=\cfrac{3}{4})$；
当$4+a\ge 0$时，即$a\ge -4$时，取$sin(\theta+\phi)=-1$，
$d_{max}=\cfrac{|-5-a-4|}{\sqrt{17}}=\cfrac{9+a}{\sqrt{17}}=\sqrt{17}$，解得$a=8$；
当$4+a< 0$时，即$a< -4$时，取$sin(\theta+\phi)=1$，
$d_{max}=\cfrac{|5-a-4|}{\sqrt{17}}=\cfrac{1-a}{\sqrt{17}}=\sqrt{17}$，解得$a=-16$。
综上所述，$a$的值为$8或-16$。

9、求轨迹方程(相关点法)

例10【求轨迹方程】
在直角坐标系$xoy$中，以坐标原点为极点，$x$轴正半轴为极轴建立极坐标系，直线$l_1$的参数方程为$\begin{cases}x=t\\y=at\end{cases}(t为参数)$，
曲线$C_1$的方程为$\rho(\rho-4sin\theta)=12$，定点$A(6，0)$，点$P$是$C_1$上的动点，$Q$为$AP$的中点，
(1)、求点$Q$的轨迹$C_2$的直角坐标方程；
(2)、直线$l$与曲线$C_2$交于$A、B$两点，若$|AB|\ge 2\sqrt{3}$，求实数$a$的取值范围；
分析：(1)【法1】：将曲线$C_1$的极坐标方程化为直角坐标方程为$x^2+y^2-4y=12$，
设点$P(x'，y')$，点$Q(x，y)$，由$Q$为$AP$的中点，
得到$\begin{cases}x'=2x-6\\y'=2y\end{cases}$，
代入$x^2+y^2-4y=12$，(此方法叫相关点法)
得到点$Q$的轨迹$C_2$的直角坐标方程为$(x-3)^2+(y-1)^2=4$；
【法2】：参数方程法，将曲线$C_1$的直角坐标方程为$x^2+y^2-4y=12$，即$x^2+(y-2)^2=16$
化为参数方程得到$\begin{cases}x=4cos\theta\\y=2+4sin\theta\end{cases}(\theta为参数)$，定点$A(6，0)$，
则其中点$Q(2cos\theta+3，1+2sin\theta)$，
即点$Q$的参数方程为$\begin{cases}x=2cos\theta+3\\y=1+2sin\theta\end{cases}(\theta为参数)$，
消去参数得到，点$Q$的轨迹$C_2$的直角坐标方程为$(x-3)^2+(y-1)^2=4$；
(2)、遇到直线和圆的位置关系问题，我们常常想到弦长半径和弦心距的$Rt\Delta$；
由题可知，直线$l$的直角坐标方程为$y=ax$，由$|AB|\ge 2\sqrt{3}$，
可得圆心$(3，1)$到直线$y=ax$的点线距$d=\sqrt{2^2-(\cfrac{2\sqrt{3}}{2})^2}\leq 1$，
即$d=\cfrac{|3a-1|}{\sqrt{a^2+1}}\leq 1$，平方得到
$(3a-1)^2\leq (a^2+1)$，解得$0\leq a\leq \cfrac{3}{4}$；
故实数$a$的取值范围为$[0， \cfrac{3}{4}]$；
例11【求轨迹方程】已知圆$C：x^2+y^2=4$，直线$l：x+y=2$，以坐标原点为极点，$x$轴正半轴为极轴建立极坐标系， (1)、将圆$C$和直线$l$的方程化为极坐标方程； 简析：$C：\rho=2$；$l：\rho(cos\theta+sin\theta)=2$ (2)、点$P$是直线$l$上的点，射线$OP$交圆$C$于点$R$，又点$Q$在$OP$上 且满足$|OQ|\cdot|OP|=|OR|^2$，当点$P$在直线$l$上移动时，求点$Q$的轨迹的极坐标方程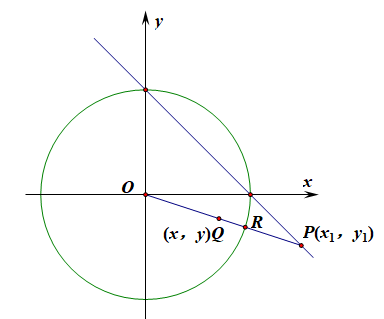； 【思路一】：碰到这样的问题，我们一般是想着在直角坐标系下进行相应的运算，然后将结果转化成极坐标系即可， 设点$P(x_1，y_1)$，点$Q(x，y)$， 这样由$|OQ|\cdot|OP|=|OR|^2$，$|OR|=2$，变形得到$\sqrt{x^2+y^2}\cdot \sqrt{x_1^2+y_1^2}=4①$， 为得到关于点$Q$的轨迹方程，需要转化去掉方程中的变量$x_1$和$y_1$， 为此我们注意到$\cfrac{x_1}{x}=\cfrac{y_1}{y}=t>0$，则 $x_1=t\cdot x$，$y_1=t\cdot y$， 代入方程①得到，$\sqrt{x^2+y^2}\cdot \sqrt{t^2x^2+t^2y^2}=4$， 即$(x^2+y^2)\sqrt{t^2}=(x^2+y^2)\cdot t=4②$ 这样就多出来了一个变量$t$，只要将他想办法去掉就可以了， 又由于$x_1+y_1=2$，即$tx+ty=2$， 这样$t=\cfrac{2}{x+y}$， 代入方程②得到，$(x^2+y^2)\cdot\cfrac{2}{x+y}=4$； 即点$Q$的轨迹方程的直角坐标方程为$x^2+y^2=2(x+y)$， 即点$Q$的轨迹方程为$\rho=2(sin\theta+cos\theta)$。 【思路二】：极坐标系法，设点$P(\rho_1，\theta)$，点$Q(\rho，\theta)$，点$R(\rho_0，\theta)$， 则有$\rho_0=2$，且$\rho_1(cos\theta+sin\theta)=2$， 则由$|OQ|\cdot|OP|=|OR|^2$，$|OR|=2$，得到$\rho\cdot \rho_1=4$， 即$\rho\cdot \cfrac{2}{cos\theta+sin\theta}=4$， 整理得到，$\rho=2(sin\theta+cos\theta)$， 即点$Q$的轨迹方程为$\rho=2(sin\theta+cos\theta)$。 解后反思： 1、通过两种思路的比较，我们基本能体会到极坐标系是有其自身的优越性的， 法1一开始是四个变量，法2一开始就只有三个变量$\rho，\rho_1，\theta$， 当将$\rho_1$做代换之后，立马就变成了两个变量，结果也就出来了。 2、由此题目我们还可以延伸思考，若给定条件是$\cfrac{|OQ|}{|OP|}=4$，或者$|OQ|\pm|OP|=4$， 那么用极坐标法都是比较简单的。

转载于:https://www.cnblogs.com/wanghai0666/p/8747722.html