矩阵分解

矩阵分解

矩阵可以分解为多个矩阵的乘积。
这些矩阵的乘积是原矩阵的低秩近似。
一个矩阵的秩一定小于这个矩阵的min(行数，列数)。
\[rank(A) \leq min(M,N)\]
矩阵的秩表达了这个矩阵张成的空间的维度，如果矩阵当前的维度比矩阵的秩大，那么说明在这个矩阵中一定包含线性相关的向量，某些向量能够用其他向量线性表示。

矩阵分解的应用

推荐系统

用户-物品矩阵，协同过滤

文本挖掘

文档-词矩阵，话题模型

社交网络

节点-节点矩阵，链接预测

常用的矩阵分解算法

SVD分解

SVD介绍

下面这篇博客介绍的很好了。
https://www.cnblogs.com/lzllovesyl/p/5243370.html
（SVD分解的并行算法？）

PCA

PCA是SVD分解的一个应用。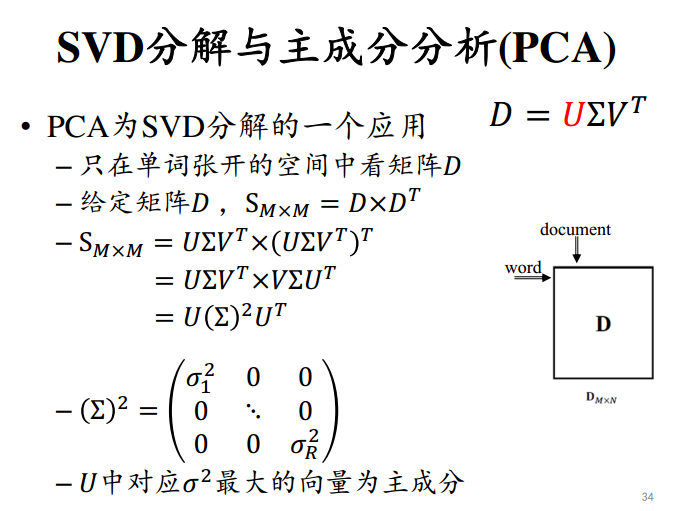

LSI（Latent Semantic Indexing）：SVD分解在文本数据上的应用

潜在语义索引，在词袋模型的假设下，将文档集合表达为【文档-词】的矩阵，每一行表示一个文档，由词袋中的词构成列。
分解之后，左特征向量U表示的是由带权的词向量表达的话题，右特征向量V表达的是由话题进行表达的文档。
LSI就是将【文档-词】矩阵进行分解，保留最大的K个特征值，其余置0。
LSI最终输出特征向量，形成话题和用话题表示的文档。
数学优美，计算难度大。
https://www.jianshu.com/p/40fbe2bdffd3

NMF分解

https://blog.youkuaiyun.com/pipisorry/article/details/52098864
D、U、V都是非负矩阵。U和V不再要求正交。
优化目标：
\[\min_{U,V}|D-U\times V^T|^2, s.t. u_{ij} \geq 0;v_{ij} \geq 0\]
目标函数为非凸函数，无全局最优解。
进行交替优化，固定U优化V，固定V优化U。

低秩近似

低秩：一些行/列可以表达为其他行列的线性组合
低秩意味着局部平滑（local smoothness）
在文本中，平滑指文档比较相似；在推荐系统中，平滑指用户购买兴趣相似。

转载于:https://www.cnblogs.com/nellyluo/p/10126503.html