tensorflow基本教程

2019独角兽企业重金招聘Python工程师标准>>>

训练神经网络有3个步骤：

    1：定义神经网络的结构和前向传播的输出结果

    2:定义损失函数以及选择反向传播优化算法

    3:生成会话，并且在训练数据上反复运行反向传播优化算法

定义一个张量：

a = tf.constant([1.0,2.0],name="a")

a的类型为：Tensor("a:0", shape=(2,), dtype=float32) 定义了a的shape纬度 和类型以及名字

取出张量的值：sess = tf.Session() sess.run(a) 输出[ 1.  2.]一维数组是a的值

TensorFlow变量

变量里面包含张量，是神经网络的参数，通过优化变量可以变到合适的值

声明：biases=tf.Variable(tf.zeros([1])) 声明了一个名字为biases的变量，变量的值是一个包含一个0的一维数组

附：常数生成函数tf.ones([2,3],int32)->[[1,1,1],[1,1,1]];  tf.fill([2,3],9)->[[9,9,9],[9,9,9]];  tf.constant([1,2,3])->[1,2,3]。都是产生数组

import numpy as np 随机数0-1生成函数：np.random.rand(2,3)生成一个2*3的数组

初始化：sess.run(biases.initializer)

取值：sess.run(biases)

神经网路：

深度学习的概念就是：定义一个输入 经过神经网络 输出一个结果。

损失函数：

 监督学习的两大类：

• 分类问题：将不同的样本划分到已知的类别当中
• 回归问题：对具体数值的预测

    1.分类问题。常用方法：交叉熵cross_entropy，它描述了两个概率分布之间的距离，当交叉熵越小说明二者之间越接近，交叉熵定义，概率q表示概率p的交叉熵为：

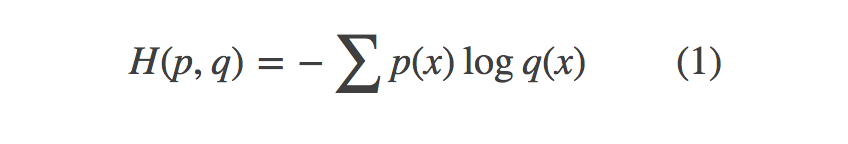
cross_entropy = -tf.reduce_mean(y_ * tf.log(tf.clip_by_value(y, 1e-10, 1.0)))

# y_:真实值，y:原始输出
# tf.reduce.mean函数求解平均数
# tf.clip_by_value函数将一个张量的数值限制在一个范围内，上面代码将 q 的值限制在(1e-10, 1.0)之间

但是，网络的输出不一定是概率分布，因此需要将网络前向传播的结果转换成概率分布。常用方法是Softmax回归.tensorflow中，Softmax回归只作为一层额外的处理层，进行概率分布的转换。转换公式： 

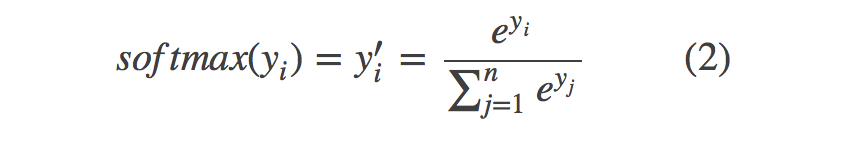
式中原始的网络输出是yi，y′i是转换后的概率分布。注意的是公式(1)并不是对称的，也即是(H(p,q))≠H(q,p)，公式(1)描述的是概率q表达概率p的困难程度。因此在神经网络的损失函数中，q代表预测值，p代表真实值。tensorflow将cross_entropy与softmax统一封装实现了softmax后的cross_entropy损失函数

cross_entropy = tf.nn.softmax_cross_entropy_with_logits(y, y_)

2.回归问题：对具体数值的预测 如房价预测、销量预测等问题需要预测的是一个任意实数，其网络输出只有一个节点，也即是预测值。

常用的损失函数：均方误差(MSE, mean squared error)

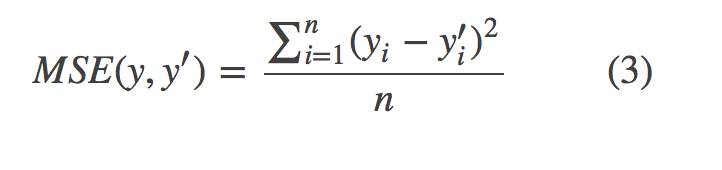
其中batch中的第i个输入的正确值记作yi，其预测值记作y′i

mse = tf.reduce.mean(tf.squared(y_ - y))
# y_:正确值，y:预测值

 

自定义损失函数

自定义的损失函数通常更加符合所应用的场景，如在销量预测中，我们对预测值与正确值之间的大小关系作为损失调整的条件，那么得到类似下面的式子： 

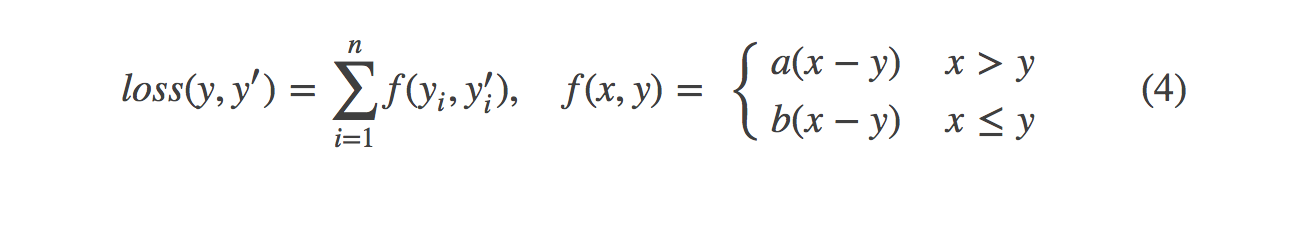
在tensorflow中实现

 

loss = tf.reduce.sum(tf.select(tf.greater(v1, v2), a*(v1-v2), b*(v1-v2)))

激活函数的作用

在神经网络中，激活函数的作用是能够给神经网络加入一些非线性因素，使得神经网络可以更好地解决较为复杂的问题。 
我们尝试引入非线性的因素，对样本进行分类。

在神经网络中也类似，我们需要引入一些非线性的因素，来更好地解决复杂的问题。而激活函数恰好就是那个能够帮助我们引入非线性因素的存在，使得我们的神经网络能够更好地解决较为复杂的问题。

常见的激活函数有Sigmoid，Relu，tanh等。 
关于上述函数的公式，在此不赘述。

Sigmoid函数如下： 

tanh函数如下：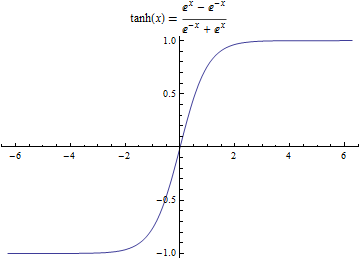 

Relu函数如下：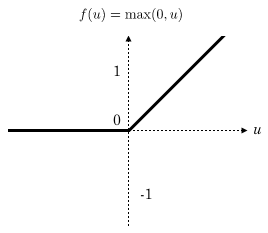 

在Tensorflow中使用激活函数 
以Relu函数为例：

import tensorflow as tf

# 默认Tensorflow会话
sess = tf.InteractiveSession()

# Relu函数处理负数
print("anwser 1:",tf.nn.relu(-2.9).eval())
# Relu函数处理正数
print("anwser 2:",tf.nn.relu(3.4).eval())

# 产生一个4x4的矩阵，满足均值为0，标准差为1的正态分布
a = tf.Variable(tf.random_normal([4,4],mean=0.0, stddev=1.0))

# 对所有变量进行初始化，这里对a进行初始化
tf.global_variables_initializer().run()

# 输出原始的a的值
print("原始矩阵:\n",a.eval())

# 对a使用Relu函数进行激活处理，将结果保存到b中
b = tf.nn.relu(a)

# 输出处理后的a，即b的值
print("Relu函数激活后的矩阵:\n",b.eval())

结果如下：（由于不同的机器，运行结果会有不同）

anwser 1: 0.0
anwser 2: 3.4
原始矩阵:
 [[-0.42271236  0.70626765  0.4220579  -1.19738662]
 [-0.09090481  1.20085275 -1.37331688 -0.28922254]
 [-0.63343877  0.04532439 -0.98322827 -0.01032094]
 [ 0.364104    1.00423157  0.23247592 -1.13028443]]
Relu函数激活后的矩阵:
 [[ 0.          0.70626765  0.4220579   0.        ]
 [ 0.          1.20085275  0.          0.        ]
 [ 0.          0.04532439  0.          0.        ]
 [ 0.364104    1.00423157  0.23247592  0.        ]]

可以发现，对于输入是一个数字来说，输出满足公式。对于输入参数是一个矩阵的情况，relu函数对矩阵中的每一个数字均使用了Relu函数进行处理，负数直接变为0.0，正数保持不变。

其他的激活函数亦是如此。

 

 

转载于:https://my.oschina.net/HeroOneHY/blog/1596614