集合论——二元关系的定义组成及性质

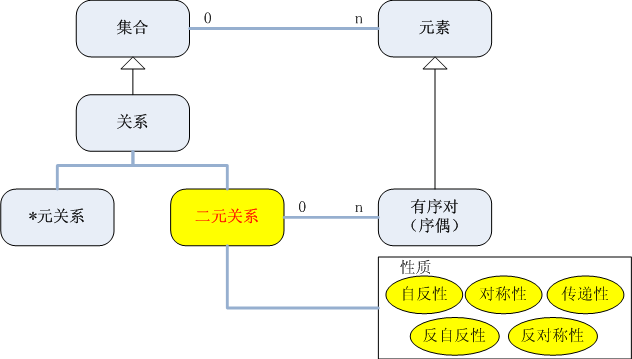
图1 二元关系的组成及性质

 

二元关系，记做R。满足以下条件：

1)        集合非空，且它的元素都是有序对

2)        集合是空集

 

由两个元素x和y按一定顺序排列成的二元组叫做一个有序对，记做<x, y>，其中x是它的第一元素，y是它的第二元素。

 

性质	定义	判定	关系矩阵判定
自反性	所有恒元都在R中	IAR	MR主对角线上的元素都为1
反自反性	所有恒元都不在R中	R∩IA =Φ	MR主对角线上的元素都为0
对称性	当<x, y>∈R， 必有<y, x>∈R	R=R-1	MR是对称矩阵
反对称性	当x≠y时，若<x, y>∈R，则必有<y, x>R	R∩R-1IA	MR中i≠j时，aij*aji=0
传递性	当<x, y>∈R且<y, z>∈R时，必有<x, z>∈R	R•RR	对于MR中每一个非零元素aij=1，将MR中第j行元素加（布尔加）到第i行上去，如果操作后，矩阵无变化

表1 二元关系的性质及其判定

 

参考文献：

[1] 俞瑞钊, 陈亮. 集合初步. 杭州: 浙江大学出版社, 2007, 12.

转载于:https://www.cnblogs.com/6DAN_HUST/archive/2009/11/16/1603671.html