matlab使用经验模式分解emd 对信号进行去噪

最新推荐文章于 2024-03-30 17:23:04 发布

转载

最新推荐文章于 2024-03-30 17:23:04 发布 · 6.2k 阅读

21 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/tecdat/p/9662540.html

文章标签：

#matlab #人工智能 #python

本文介绍了如何在MATLAB中利用经验模式分解(EMD)对包含明显频率变化的非平稳信号进行去噪。通过可视化残余和内在模式功能，展示了EMD在识别和分离不同频率成分方面的效果，适用于分析如手提钻振动或烟花声等非平稳信号。

对于这个例子，考虑由具有明显频率变化的正弦波组成的非平稳连续信号。手提钻的振动或烟花声是非平稳连续信号的例子。

以采样频率加载非平稳信号数据fs，并可视化混合正弦信号。

load（'sinusoidalSignalExampleData.mat'，'X'，'fs'）; 
 
xlabel（'Time（s）'）;

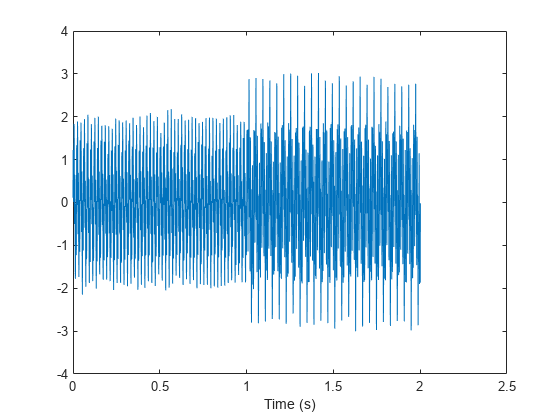
观察到混合信号包含具有不同幅度和频率值的正弦波。

为了创建希尔伯特谱图，您需要信号的IMF。执行经验模式分解以计算信号的固有模式函数和残差。由于信号不平滑，请指定' pchip'作为Interpolation方法。

[imf，residual，info] = emd（X，'Interpolation'，'pchip'）;

目前的IMF | #Sift Iter | 相对Tol | 停止标准命中   
      1 | 2 | 0.026352 | SiftMaxRelativeTolerance 
      2 | 2 | 0.0039573 | SiftMaxRelativeTolerance 
      3 | 1 | 0.024838 | SiftMaxRelativeTolerance 
      4 | 2 | 0.05929 | SiftMaxRelativeTolerance 
      5 | 2 | 0.11317 | SiftMaxRelativeTolerance 
      6 | 2 | 0.12599 | SiftMaxRelativeTolerance 
      7 | 2 | 0.13802 | SiftMaxRelativeTolerance 
      8