导数章节中的题型和对应求解思路【三轮总结】

一、知识储备：

• 本节用到的数学思想：分类讨论；转化划归；数形结合；函数与方程；

• 本节用到的数学方法：导数法，多项式除法，试商法，分组分解法，分离参数法，

• 恒成立、能成立类命题

二、题型归类：

题型Ⅰ：求曲线$f(x，y)=0$或函数$y=f(x)$的切线类型1：一曲线一直线的单切线形、 思路方法：若是在点处，利用点斜式写出切线方程：$y-f(x_0)=f'(x_0)(x-x_0)$；若是过点处，则设切点$(x_0，y_0)$，然后利用方程组求切点，再代入计算切线即可。 例1【2017全国卷1文科第14题高考真题】曲线$y=x^2+\frac{1}{x}$在点$(1，2)$处的切线方程是__________。
例2【过点处】：求曲线$C:y=\cfrac{1}{3}x^3+\cfrac{4}{3}$经过点$P(2，4)$的切线方程；（$4x-y-4=0$或$x-y+2=0$） 【例1】分析：利用点斜式来求解， 其中斜率$k=f'(x)_{|x=1}=(2x-\cfrac{1}{x^2})_{|x=1}=1$， 切点是$(1，2)$， 故切线方程为$y-2=1(x-1)$，整理为$y=x+1$。 【例2】分析：设经过点$P(2，4)$的切线方程与曲线相切于点$P_0(x_0，y_0)$，则有 $\begin{cases}y_0=\cfrac{1}{3}x_0^3+\cfrac{4}{3}\\ k=f'(x_0)=x_0^2\\ y-y_0=f'(x_0)(x-x_0) \end{cases}$ 又因为点$P(2，4)$在切线方程上，则有$4-(\cfrac{1}{3}x_0^3+\cfrac{4}{3})=x_0^2(2-x_0)$ 整理得到，$x_0^3-3x_0^2+4=0$ $x_0^3-3x_0^2+4=(x_0^3+1)-3(x_0^2-1)$ $=(x_0+1)(x_0^2-x_0+1)-3(x_0+1)(x_0-1)$ $=(x_0+1)(x_0^2-x_0+1-3x_0+3)$ $=(x_0+1)(x_0-2)^2=0$； 即$(x_0+1)(x_0-2)^2=0$，解得$x_0=-1$，或$x_0=2$ 当$x_0=-1$时，切点为$(-1，1)$，$k_1=1$，切线方程为$x-y+2=0$； 当$x_0=2$时，切点为$(2，4)$，$k_2=4$，切线方程为$4x-y-4=0$； 注意：常用的变形方法有试商法、分组分解法、多项式除法；
类型2：两曲线一直线的公切线型、 思路方法：转化为一曲线和一直线型；或者利用同一法求解 例3(2017•潍坊模拟) 若存在过点$(1，0)$的直线与曲线$y＝x^3$和$y＝ax^2+\cfrac{15}{4}x-9$都相切，则$a$等于【 】
A、$-1$或$-\cfrac{25}{64}$ $\hspace{2cm}$ B、$-1$或$-\cfrac{21}{4}$ $\hspace{2cm}$
C、$-\cfrac{7}{4}$或$-\cfrac{25}{64}$ $\hspace{2cm}$ D、 $-\cfrac{7}{4}$或$7$
分析：本题目属于公切线问题，可以先求得过点处的与$y=x^3$相切的直线，
然后联立直线和抛物线(二次函数)，利用$\Delta=0$来解决。
设过点$(1，0)$的直线与曲线$y＝x^3$相切于点$(x_0，y_0)$，由$f'(x)=3x^2$可得，
$\begin{cases}k=f'(x_0)=3x_0^2 \\y_0=x_0^3 \\y-y_0=f'(x_0)(x-x_0) \end{cases}$，又点$(1，0)$在切线上，故有$0-x_0^3=3x_0^2(1-x_0)$，
解得$x_0=0$或$x_0=\cfrac{3}{2}$；
当$x_0=0$时，$y_0=0$，即切点是$(0，0)$，斜率$k=0$，故切线方程为$y=0$，
与曲线$y=ax^2+\cfrac{15}{4}x-9$相切，消$y$得到$ax^2+\cfrac{15}{4}x-9=0$，
利用$\Delta=(\cfrac{15}{4})^2+4\times 9a=0$，解得$a=-\cfrac{25}{64}$；
当$x_0=\cfrac{3}{2}$时，$y_0=\cfrac{27}{8}$，即切点是$(\cfrac{3}{2}，\cfrac{27}{8})$，斜率$k=\cfrac{27}{4}$，
故切线方程为$y-\cfrac{27}{8}=\cfrac{27}{4}(x-\cfrac{3}{2})$，
与曲线$y=ax^2+\cfrac{15}{4}x-9$相切，消$y$得到$ax^2-3x-\cfrac{9}{4}=0$，
利用$\Delta=(-3)^2-4\times a\times(-\cfrac{9}{4})=0$，解得$a=-1$；
综上，$a=-1$或$-\cfrac{25}{64}$，故选A。
反思总结：直线与三次曲线的相切问题，我们用导数解决；
直线与二次曲线(如圆、椭圆、双曲线、抛物线等)的相切问题，我们常用$\Delta=0$来解决。
题型Ⅱ：求函数$y=f(x)$的单调区间或判断单调性类型1：数字系数的函数的单调性的求解或证明 思路方法：转化为数字系数的不等式的求解，求解过程可以借助导函数的图像或者导函数的分子图像或者导函数的组成部分的图像，以形助数，简化求解； 例1已知函数$f(x)=2x^3+ax^2+bx+1$的导函数为$f'(x)$，若函数$y=f'(x)$的对称轴是$x=-\cfrac{1}{2}$，且$f'(1)=0$
(1).求$a，b$的值。
(2).判断函数的单调性，并求函数的极值。
【分析】(1)通过导函数方程和二次函数对称轴方程建立方程组，即可解得a、b，
(2)数字系数的三次多项式函数求极值，用常规的思路和步骤求解即可。
【解答】(1)由于$f'(x)=6x^2+2ax+b$，且对称轴为$x=-\cfrac{1}{2}$，
则有$-\cfrac{a}{6}=-\cfrac{1}{2}$，则$a=3$，
又由于$f'(1)=0$，则$6+2a+b=0$，解得$b=-12$，
所以$a=3，b=-12$。
(2)因为$f(x)=2x^3+3x^2-12x+1$，$f'(x)=6x^2+6x-12=6(x^2+x-2)$

常规的解法这样写道： 令$f'(x)≥0$，即$x^2+x-2≥0$，解得$x≥1$或$x≤-2$，
令$f'(x) ≤0$，即$x^2+x-2 ≤0$，解得$ -2≤x ≤1$，
有了辅助图像后，我们这些写：
当$x< -2$时，$f'(x)>0$，$f(x)$单调递增；
当$-2 当$x>1$时，$f'(x)>0$，$f(x)$单调递增；
然后做总结：
所以函数$f(x)$在$(-2，1)$上单调递减，在$(-\infty，-2)$和$(1，+\infty)$上单调递增，
当$x=-2$时，$f(x)$取得极大值，为$f(-2)=21$，
当$x=1$时，$f(x)$取得极小值，为$f(1)=-6$。
类型2：字母系数的函数的单调性的求解 思路方法：转化含参不等式的求解，难点是分类讨论和数形结合 例2已知函数$f(x)=x^2+2mlnx-(m+4)x+lnm+2$，当$m＞0$时，试讨论函数$f(x)$的单调性；
【分析】借助导函数的分子函数的动态图像，即可判断导函数的正负，从而判断原函数的单调性。
【解答】辅助图像
$f'(x)=2x+\cfrac{2m}{x}-(m+4)=\cfrac{2x^2-(m+4)x+2m}{x}=\cfrac{(x-2)(2x-m)}{x}$，
令$f'(x)=0$，得到$x=2$或$x=\cfrac{m}{2}>0$，只需要借助分子函数的图像，即可判断导函数的正负，
当$00$，$f(x)$单调递增，
$x\in (\cfrac{m}{2}，2)$时，$f'(x)<0$，$f(x)$单调递减，$x\in (2，+\infty)$时，$f'(x)>0$，$f(x)$单调递增，
当$\cfrac{m}{2}=2$时，即$m=4$时，此时$f'(x)\ge 0$恒成立，
当且仅当$x=2$时取得等号，故$f(x)$在$(0，+\infty)$上单调递增，
当$\cfrac{m}{2}>2$时，即$m >4$时， $x\in (0，2)$时，$f'(x) >0$，$f(x)$单调递增，
$x\in (2，\cfrac{m}{2})$时，$f'(x) <0$，$f(x)$单调递减， $x\in (\cfrac{m}{2}，+\infty)$时，$f'(x) >0$，$f(x)$单调递增，
综上所述，
当$0< m <4$时， $x\in (0，\cfrac{m}{2})$时，$f(x)$单调递增，
$x\in (\cfrac{m}{2}，2)$时，$f(x)$单调递减，
$x\in (2，+\infty)$时，$f(x)$单调递增，
当$m=4$时，$f(x)$在$(0，+\infty)$上单调递增，
当$m >4$时， $x\in (0，2)$时，$f(x)$单调递增，
$x\in (2，\cfrac{m}{2})$时，$f(x)$单调递减，
$x\in (\cfrac{m}{2}，+\infty)$时，$f(x)$单调递增，
题型Ⅲ：已知函数$y=f(x)$的单调性，求参数的取值范围类型1：参数包含在函数的系数中 思路方法：若函数$y=f(x)$在区间$[a，b]$单调递增，则$f'(x)\ge 0$在区间$[a，b]$上恒成立，且导函数$f'(x)$不恒为$0$；若函数$y=f(x)$在区间$[a，b]$单调递减，则$f'(x) \leq 0$在区间$[a，b]$上恒成立，且导函数$f'(x)$不恒为$0$；
易错警示：漏掉等号，忘掉验证； 例1【2019高三理科数学资料用题】 设函数$f(x)=(x+a)e^{ax}(a\in R)$，若函数在区间$(-4，4)$内单调递增，求$a$的取值范围。
【解答】由函数$f(x)$在在区间$(-4，4)$内单调递增，
则$f'(x)\ge 0$在区间$(-4，4)$内恒成立，
又$f'(x)=(ax+a^2+1)e^{ax}$，注意到$e^{ax}>0$恒成立，
即有$ax+a^2+1\ge 0$在区间$(-4，4)$内恒成立，
令$g(x)=ax+a^2+1$为一次型的函数，故只需要满足$\left\{\begin{array}{l}{g(-4)\ge 0}\\{g(4)\ge 0}\end{array}\right.$，
即$\left\{\begin{array}{l}{a^2-4a+1\ge 0}\\{a^2+4a+1\ge 0}\end{array}\right.$， 解得，$\left\{\begin{array}{l}{a\ge 2+\sqrt{3}或a\leq 2-\sqrt{3}}\\{a\leq -2-\sqrt{3}或a\ge -2+\sqrt{3}}\end{array}\right.$，
即$a\in (-\infty，-2-\sqrt{3}]\cup[-2+\sqrt{3}，2-\sqrt{3}]\cup[2+\sqrt{3}，+\infty)$。
类型2：参数包含在给定区间端点处 思路方法：用常规方法求出单调区间，那么给定区间必然是求出的单调区间的子区间，转化为集合的关系求解； 例2寻找 待解答 题型Ⅳ：函数$y=f(x)$存在单调区间，求参数的取值范围类型1：参数包含在函数的系数中 直接法：函数$y=f(x)$在区间$[a，b]$上存在单调递增区间，则$f'(x)>0$在区间$[a，b]$上能成立(或有解)；
函数$y=f(x)$在区间$[a，b]$上存在单调递减区间，则$f'(x)<0$在区间$[a，b]$上能成立(或有解)；易错警示：多添等号；
间接法：不存在单调递增区间，则函数为常函数或单调递减，则恒有$f‘(x)=0$或$f'(x)\leq 0$在区间$[a，b]$上恒成立；
不存在单调递减区间，则函数为常函数或单调递增，则恒有$f'(x)=0$或$f'(x)\ge 0$在区间$[a，b]$上恒成立； 例1【2019高三理科数学资料用题】【2018荆州模拟改编】 设函数$f(x)=\cfrac{1}{3}x^3-\cfrac{a}{2}x^2+1$，函数$g(x)=f(x)+2x$，且$g(x)$在区间$(-2，-1)$内存在单调递减区间，求实数$a$的取值范围； 【法1，直接法】：$g(x)=\cfrac{1}{3}x^3-\cfrac{a}{2}x^2+1+2x$，则$g'(x)=x^2-ax+2$，
由$g(x)$在区间$(-2，-1)$内存在单调递减区间，得到，
$g'(x)=x^2-ax+2<0$在区间$(-2，-1)$上能成立，
分离参数得到，$a < x+\cfrac{2}{x}$在区间$(-2，-1)$上能成立，
而$\left(x+\cfrac{2}{x}\right)_{max}=-2\sqrt{2}$，当且仅当$x=\cfrac{2}{x}$，即$x=-\sqrt{2}$时取到等号，
故实数$a$的取值范围为$(-\infty，-2\sqrt{2})$。
注意：存在单调递减区间，应该得到$f'(x)<0$能成立，而不是$f'(x)\leq 0$能成立。
若$a=-2\sqrt{2}$，由$g'(x)=x^2+2\sqrt{2}x+2=(x+\sqrt{2})^2\ge 0$恒成立，则函数$g(x)$只能有单调递增区间，不会存在单调递减区间。
【法2，间接法】假设函数$g(x)$在区间$(-2，-1)$内不存在单调递减区间，
则函数$g(x)$在区间$(-2，-1)$内为常函数或单调递增，
则恒有$g'(x)=0$或$g'(x)\ge 0$在区间$(-2，-1)$内恒成立，
由于$g'(x)=x^2-ax+2$，显然恒有$g'(x)=0$不成立，
故重点探究$g'(x)\ge 0$在区间$(-2，-1)$内恒成立，
$g'(x)=x^2-ax+2\ge 0$在区间$(-2，-1)$内恒成立，分离参数，
得到$a\ge x+\cfrac{2}{x}(-2< x 由于$h(x)=x+\cfrac{2}{x}$在$(-2，-\sqrt{2}]$上单调递增，在$[-\sqrt{2}，-1)$上单调递减，
故$h(x)_{max}=h(-\sqrt{2})=-2\sqrt{2}$，
故函数$g(x)$在区间$(-2，-1)$内不存在单调递减区间时，$a\ge -2\sqrt{2}$；
即存在单调递减区间时，$a< -2\sqrt{2}$，即$a\in (-\infty，-2\sqrt{2})$。
类型2：参数包含在给定区间端点处 思路方法：用常规方法求出单调区间，转化为集合的关系求解； 例2待寻找 【分析】待解答 题型Ⅴ：已知函数的极值点或者最值点，求参数的取值范围类型1：已知函数的极值点或最值点 思路方法：①针对参数分类讨论，注意结合题目中的有效信息； ②数形结合法，则函数$y=f'(x)$有变号零点，接下来数形结合求解或分离参数求解； 例1【2019届高三理科数学资料用题】 设函数$f(x)=\cfrac{e^x}{x^2}-k(\cfrac{2}{x}+lnx)$，($k$为常数)， (1)当$k\leq 0$时，求函数$f(x)$的单调区间； (2)若函数$f(x)$在$(0，2)$内存在两个极值点，求$k$的取值范围。 (1)当$k\leq 0$时，求函数$f(x)$的单调区间； 分析：函数的定义域为$(0，+\infty)$， $f'(x)=\cfrac{e^x\cdot x^2-e^x\cdot 2x}{x^4}-k(-\cfrac{2}{x^2}+\cfrac{1}{x})$ $=\cfrac{e^x(x-2)}{x^3}-\cfrac{kx(x-2)}{x^3}=\cfrac{(x-2)(e^x-kx)}{x^3}$ 【将上述分式看成三个部分，$y=x-2$和$y=e^x-kx$和$y=x^3$，每一个部分的正负必然会影响和决定整体的正负】 注意到$x^3>0$，当$k\leq 0$时，$e^x-kx>0$，故我们只需要借助$y=x-2(x>0)$的图像，就可以判断$f'(x)$的正负。 当$x\in (0，2)$时，$f'(x)<0$，$f(x)$单调递减； 当$x\in (2，+\infty)$时，$f'(x)>0$，$f(x)$单调递增； 故单减区间为$(0，2)$，单增区间为$(2，+\infty)$。 (2)若函数$f(x)$在$(0，2)$内存在两个极值点，求$k$的取值范围。 法1：分类讨论法，
由(1)知，当$k\leq 0$时，函数$f(x)$在$(0，2)$内单调递增，
故$f(x)$在$(0，2)$内不存在极值点；
当$k > 0$时，设函数$g(x)=e^x-kx$，$x\in (0，+\infty)$，
由于$g'(x)=e^x-k=e^x-e^{lnk}$，
当$x\in (0，2)$时，$e^x \in (1，e^2)$，先考虑$g'(x)\ge 0$的情形，故由此找到分点$k=1$；
当$0< k \leq 1$时，$x\in (0，2)$时，$g'(x)=e^x-k >0$，
$y=g(x)$单调递增，故$g(x)_{min}=g(0)=1>0$；
故函数$f(x)$在$(0，2)$内单调递减，故不存在极值点；
当$k >1$时，则$x\in (0，lnk)$时，$g'(x)<0$，$g(x)$单调递减，
$x\in (lnk，+\infty)$时，$g'(x) >0$，$g(x)$单调递增，
所以函数$y=g(x)$的最小值为$g(lnk)=k(1-lnk)$，
那么函数$f(x)$在$(0，2)$内存在两个极值点应该等价于函数$g(x)$在$(0，2)$内存在两个极值点，
函数$g(x)$在$(0，2)$内存在两个极值点当且仅当
$\left\{\begin{array}{l}{g(0) >0}\\{g(lnk) <0}\\{g(2)>0}\\{0< lnk <2}\end{array}\right.$

即$\left\{\begin{array}{l}{e^0-0>0}\\{k(1-lnk) <0}\\{e^2-2k >0}\\{0< lnk <2}\end{array}\right.$
解得$e< k 综上所述，函数$f(x)$在$(0，2)$内存在两个极值点，则$k\in (e，\cfrac{e^2}{2})$。
法2：由于函数$f(x)$在$(0，2)$内存在两个极值点， 则函数$y=f'(x)$在区间$(0，2)$内存在两个零点，且为变号零点， 又$f'(x)=\cfrac{(x-2)(e^x-kx)}{x^3}$，则方程$f'(x)=\cfrac{(x-2)(e^x-kx)}{x^3}=0$在$(0，2)$内有两个不同的实根， 由于$x\in (0，2)$，即方程$e^x-kx=0$在$(0，2)$内有两个不同的实根， 分离参数，即方程$k=\cfrac{e^x}{x}$在$(0，2)$内有两个不同的实根， 即函数$y=k$和函数$h(x)=\cfrac{e^x}{x}$的图像在$(0，2)$内有两个不同的交点， 函数$y=h(x)$的定义域为$(-\infty，0)\cup(0，+\infty)$， 由于$h'(x)=\cfrac{e^x\cdot x-e^x\cdot 1}{x^2}=\cfrac{e^x(x-1)}{x^2}$， 故$x\in (-\infty，0)$时，$h'(x)<0$，$h(x)$单调递减， $x\in (0，1)$时，$h'(x)<0$，$h(x)$单调递减， $x\in (1，+\infty)$时，$h'(x)>0$，$h(x)$单调递增， 又由于$h(1)=e$，根据以上做出函数$h(x)$的简图如下， 注意，本题目中只需要关注$h(x)$的$x\in (0，2)$这一段， 由图像可知，两个函数的图像要有两个不同的交点，则$k\in (e，\cfrac{e^2}{2})$。 故函数$f(x)$在$(0，2)$内存在两个极值点，则$k\in (e，\cfrac{e^2}{2})$。 类型2：已知函数的极值或最值 思路方法：已知函数的极值或最值，常常向讨论函数的单调性方向转化 例2待寻找 【分析】 题型Ⅵ：已知函数$f(x)$的零点个数，求参数的取值范围类型1：给定函数的零点个数 思路方法：常考虑①利用已有的单调性分类讨论确定参数的范围；②不完全分离参数法；③完全分离参数法； 例1【2017西安模拟】已知函数$f(x)=kx^2-lnx$有两个零点，求参数$k$的取值范围。 A、$k>\cfrac{e}{2}$ $\hspace{2cm}$ B、$0< k\cfrac{\sqrt{2}e}{2}$ $\hspace{2cm}$ D、 $0< k 【解答】 【法1】：数形结合法，定义域为$(0，+\infty)$，转化为方程$kx^2=lnx$有两个不同的实数根， 再转化为函数$y=kx^2$与函数$y=lnx$的图像有两个不同的交点， 如图设两个函数的图像相切于点为$(x_0，y_0)$， 则有关系式$\begin{cases}2kx_0=\cfrac{1}{x_0}\\kx_0^2=y_0\\y_0=lnx_0\end{cases}$， 解得$y_0=\cfrac{1}{2}，x_0=\sqrt{e}$，即切点为$(\sqrt{e}，\cfrac{1}{2})$， 再代入函数$y=kx^2$，求得此时的$k=\cfrac{1}{2e}$， 再结合函数$y=kx^2$的系数$k$的作用，可得两个函数要有两个不同的交点， 则$k\in(0，\cfrac{1}{2e})$。 【法2】：分离参数法，定义域为$(0，+\infty)$，转化为方程$kx^2=lnx$有两个不同的实数根， 再转化为$k=\cfrac{lnx}{x^2}$有两个不同的实数根， 再转化为函数$y=k$和函数$y=g(x)=\cfrac{lnx}{x^2}$的图像有两个不同的交点， 用导数研究函数$g(x)$的单调性，$g'(x)=\cfrac{\cfrac{1}{x}\cdot x^2-lnx\cdot 2x}{(x^2)^2}=\cfrac{1-2lnx}{x^3}$， 令$1-2lnx>0$，得到$0< x\sqrt{e}$， 即函数$g(x)$在区间$(0，\sqrt{e}]$上单调递增，在$[\sqrt{e}，+\infty)$上单调递减， 故$g(x)_{max}=g(\sqrt{e})=\cfrac{1}{2e}$， 作出函数$g(x)$和函数$y=k$的简图，由图像可得$k$的取值范围是$k\in(0，\cfrac{1}{2e})$。 类型2： 思路方法： 例2待寻找 【分析】 题型Ⅶ：已知函数$f(x)$有极值，求参数的取值范围类型1：含参函数$f(x)$有极值， 思路方法：常考虑函数$y=f'(x)$有变号零点，再数形结合转化有交点或分离参数转化有解 例1已知$|\vec{a}|=2|\vec{b}|$，$|\vec{b}| \neq 0$，且关于$x$的函数$f(x)=\cfrac{1}{3}x^3+\cfrac{1}{2}|\vec{a}|x^2+\vec{a}\cdot \vec{b}x$在$R$上有极值，则$\vec{a}$与$\vec{b}$的夹角范围是【】
$A、[0，\cfrac{\pi}{6})$；$B、(\cfrac{\pi}{3}，\pi]$；$C、(\cfrac{\pi}{3}，\cfrac{2\pi}{3}]$；$D、(\cfrac{\pi}{6}，\pi]$；
分析：函数$f(x)=\cfrac{1}{3}x^3+\cfrac{1}{2}|\vec{a}|x^2+\vec{a}\cdot \vec{b}x$在$R$上有极值，
其充要条件是其导函数$y=f'(x)$存在变号零点，
$f'(x)=x^2+|\vec{a}|x+\vec{a}\cdot \vec{b}$，其$\Delta =|\vec{a}|^2-4\vec{a}\cdot \vec{b}>0$，
设$\vec{a}$与$\vec{b}$的夹角为$\theta$，
则$4|\vec{b}|^2-4\times 2|\vec{b}| \cdot |\vec{b}| cos\theta>0$，
即$cos\theta 所以$\theta \in (\cfrac{\pi}{3}，\pi]$，故选$B$。
类型2：含参函数$f(x)$有且仅有一个有极值 思路方法：常考虑函数$y=f'(x)$有且仅有一个变号零点，再数形结合转化为仅有一个交点或分离参数转化有解； 例2若函数$f(x)=x^4-ax^3+x^2-2$有且仅有一个极值点，则实数$a$的取值范围是___________。
分析：$f'(x)=4x^3-3ax^2+2x=x(4x^2-3ax+2)$，
函数$f(x)=x^4-ax^3+x^2-2$有且仅有一个极值点，
其充要条件是因子函数$h(x)=4x^2-3ax+2$不存在变号零点，
即$\Delta=9a^2-32\leq 0$，解得$-\cfrac{4\sqrt{2}}{3}\leq x\leq \cfrac{4\sqrt{2}}{3}$，
即$a\in [-\cfrac{4\sqrt{2}}{3}，\cfrac{4\sqrt{2}}{3}]$。
题型Ⅷ：已知方程$a=f(x)$有$n$个根，求参数的取值范围类型1：给定或能转化为形如方程$a=f(x)$有$n$个根 思路方法：需要将所给的题目转化为上述方程有$n$个根的形式，难点是利用导数或其他方法做出函数$f(x)$的图像，数形结合求解即可。 例1【已知方程的零点个数，求参数的取值范围】【2019届高三理科函数与方程课时作业第16题改编】
已知函数$f(x)=\left\{\begin{array}{l}{x^2-2x，x\ge 0}\\{-x^2-2x，x<0}\end{array}\right.$，若方程$f(x)=a$恰有$3$个不同的解，求$a$的取值范围。
分析：转化为函数$y=f(x)$和函数$y=3$的图像恰有$3$个不同的交点，
做出两个函数的图像，由图像可知，要使其有$3$个不同的交点，
只需要$-1< a <1$，故$a\in (-1，1)$。
类型2：函数$g(x)=f(x)-a$有$n$个不同的零点，可以转化为类型1 思路方法： 例2例题待寻找 【分析】 题型Ⅸ：已知$a=f(x)$有解或无解，求参数的取值范围类型1：给定方程$a=f(x)$有解或能转化为方程有解 思路方法：求解行不通时就数形结合；即函数$y=a$和函数$y=f(x)$的图像有交点，难点：①能顺利转化为本类型；②做函数$f(x)$的图像； 例1已知函数 【解答】 类型2：给定方程$a=f(x)$无解或能转化为方程无解 思路方法：求解行不通时就数形结合；即函数$y=a$和函数$y=f(x)$的图像无交点，难点：①能顺利转化为本类型；②做函数$f(x)$的图像； 例2【例题】 【分析】 题型Ⅹ：函数$y=f(x)$在区间$(a，b)$上单调或不单调，求参数的取值范围类型1：函数$y=f(x)$在区间$(a，b)$上单调 思路方法：①分类讨论，单调递增时，$f'(x)\ge 0$恒成立；单调递减时，$f'(x)\leq 0$恒成立；结果求并集；
②直接法，由于函数单调，则$y=f'(x)$无零点，或有不变号零点，再转化为方程$f'(x)=0$无解或有切点解的形式。 例1函数$f(x)=\cfrac{1}{3}x^3-x^2+ax-5$在区间$[-1，2]$上单调，则实数$a$的取值范围是_________。 法1：分类讨论法，$f'(x)=x^2-2x+a$，
若函数$f(x)$在$[-1，2]$上单增，则$f'(x)=x^2-2x+a\ge 0$恒成立， 分离参数得到$a\ge -x^2+2x$恒成立，
在$[-1，2]$上求得函数$f(x)_{max}=1$，故$a\ge 1$；
若函数$f(x)$在$[-1，2]$上单减，则$f'(x)=x^2-2x+a\leq 0$恒成立，
分离参数得到$a\leq -x^2+2x$恒成立，
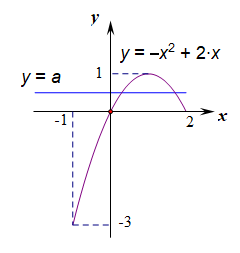在$[-1，2]$上求得函数$f(x)_{min}=-3$，故$a\leq -3$；
故当$a\in (-\infty，-3]\cup[1，+\infty)$时，函数$f(x)$在区间$[-1，2]$上单调。
法2：直接法，由于函数$f(x)=\cfrac{1}{3}x^3-x^2+ax-5$在区间$[-1，2]$上单调，
则函数$y=f'(x)$在区间$[1，2]$上无零点，
即方程$f'(x)=x^2-2x+a=0$在区间$[1，2]$上无解，
即方程$a=-x^2+2x$在区间$[1，2]$上无解，
由图像可知，$f'(x)$的值域为$[-3，1]$，
故方程$f'(x)=0$无解时得到，$a < -3$或$a >1$，
由于上述的转化是不等价的，以下检验端点值是否满足题意。
当$a=-3$时，$f'(x)=x^2-2x-3=(x+1)(x-3)$，此时若$x\in [-1，2]$，
则有$f'(x)\leq 0$恒成立，故函数$f(x)$在区间$[-1，2]$上单调递减，
符合题意，添加$a=-3$；
当$a=1$时，$f'(x)=x^2-2x+1=(x-1)^2$，此时若$x\in [-1，2]$，
则有$f'(x)\ge 0$恒成立，故函数$f(x)$在区间$[-1，2]$上单调递增，
符合题意，添加$a=1$；
综上所述，函数$f(x)=\cfrac{1}{3}x^3-x^2+ax-5$在区间$[-1，2]$上单调，
则实数$a$的取值范围是$a\in (-\infty，-3]\cup[1，+\infty)$。 类型2：函数$y=f(x)$在区间$(a，b)$上不单调 思路方法：①补集法，先求在区间$(a，b)$上单调时的参数范围，再求其补集
②直接法，函数不单调，则$y=f'(x)$有变号零点，则方程$f'(x)=0$有解，且为变号解的形式； 例2 函数$f(x)=\cfrac{1}{3}x^3-x^2+ax-5$在区间$[-1，2]$上不单调，则实数$a$的取值范围是_________。 $(-3，1)$ 法1：补集思想，$f'(x)=x^2-2x+a$，
若函数$f(x)$在$[-1，2]$上单增，则$f'(x)=x^2-2x+a\ge 0$恒成立，
分离参数得到$a\ge -x^2+2x$恒成立，
在$[-1，2]$上求得函数$f(x)_{max}=1$，故$a\ge 1$；
若函数$f(x)$在$[-1，2]$上单减，则$f'(x)=x^2-2x+a\leq 0$恒成立，
分离参数得到$a\leq -x^2+2x$恒成立，
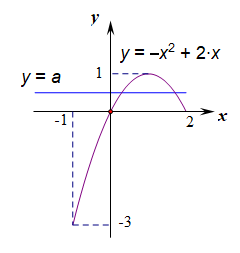在$[-1，2]$上求得函数$f(x)_{min}=-3$，故$a\leq -3$；
故取其补集，当$-3< a <1$时，函数$f(x)$在区间$[-1，2]$上不单调。
法2：直接法，由题可知$f(x)$不单调，则导函数$y=f'(x)$在区间$[-1，2]$上至少有一个变号零点，
当只有一个变号零点时，由$f'(-1)\cdot f'(2)\leq 0$可得，$-3\leq a\leq 0$；
当有两个变号零点时，由$\begin{cases}f'(-1)>0\\f'(2)>0\\\Delta >0\end{cases}$，解得$0< a < 1$；
综上所述，实数$ a $的取值范围是$(-3，1)$。
法3：(转化为方程有解类型求解)由法2可知，导函数$y=f'(x)$在区间$[-1，2]$上至少有一个变号零点，
即方程$f'(x)=0$至少有一个解，故$a=-x^2+2x$在$[-1，2]$上至少有一个解，
到此转化为方程有解类型，需要求函数的值域。
需要求出函数$y=-x^2+2x，x\in [-1，2]$上的值域$[-3，1]$，
由于上述的转化过程不是等价的，故需要检验。
当$a=-3$时，$f'(x)=x^2-2x-3=(x+1)(x-3)$，此时若$x\in [-1，2]$，
则有$f'(x)\leq 0$恒成立，故函数$f(x)$在区间$[-1，2]$上单调递减，
不符合题意，舍去；
当$a=1$时，$f'(x)=x^2-2x+1=(x-1)^2$，此时若$x\in [-1，2]$，
则有$f'(x)\ge 0$恒成立，故函数$f(x)$在区间$[-1，2]$上单调递增，
不符合题意，舍去；
故实数$a$的取值范围是$(-3，1)$。

转载于:https://www.cnblogs.com/wanghai0666/p/9940432.html