本文详细介绍了K-means聚类算法的工作原理与实现细节，包括算法步骤、质心初始化方法、距离度量方式等内容，并探讨了离群点处理、初始质心选择等问题。
前记
Kmeans是最简单的聚类算法之一，但是运用十分广泛，最近看到别人找实习笔试时有考到Kmeans，故复习一下顺手整理成一篇笔记。Kmeans的目标是：把n 个样本点划分到k 个类簇中，使得每个点都属于离它最近的质心对应的类簇，以之作为聚类的标准。质心，是指一个类簇内部所有样本点的均值。
算法描述
Step 1. 从数据集中随机选取K个点作为初始质心
将每个点指派到最近的质心，形成k个类簇
Step 2. repeat
重新计算各个类簇的质心(即类内部点的均值)
重新将每个点指派到最近的质心，形成k个类簇
until 质心不再波动例如下图的样本集，我们目标是分成3个类簇，初始随机选择的3个质心比较集中，但是迭代4次之后，质心趋于稳定，并将样本集分为3部分。
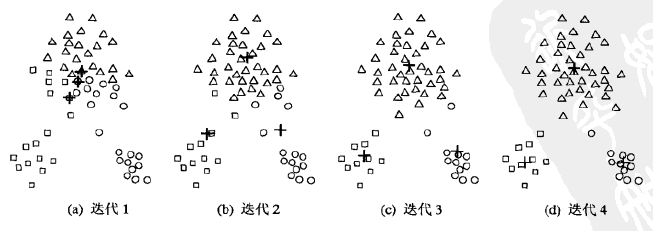
Kmeans算法，对于距离度量可以使用余弦相似度，也可以使用欧式距离或其它标准；质心，是指一个类簇内部所有样本点的均值；随机初始化的质心，当随机效果不理想时，Kmeans算法的迭代次数变多。Kmeans算法思想比较简单，但实用。
代码实现
package kmeans;
public class Point {
public double[] x; // 特征维度
public int len_arr; // 特征维数
public boolean isSample = false; // True判断是数据集的点，False是第二次kmenas所计算得来的质心
public int id; // 质心分配的id=0
public String text; // 用于描述鸢尾花种类
public Point(double[] x, int len_arr, boolean isSample, int id) {
this.x = x;
this.len_arr = len_arr;
this.isSample = isSample;
this.id = id;
}
// 计算欧氏距离
public double Distance(Point other) {
double sum = 0;
for (int i = 0; i < len_arr; i++) {
sum += Math.pow(x[i] - other.x[i], 2);
}
sum = Math.sqrt(sum);
return sum;
}
// 以下两个方法用于数据结构Set, 第一次kmeans生成k个随机点时用到
@Override
public boolean equals(Object other) {
if (other.getClass() != Point.class) {
return false;
}
return id == ((Point) other).id;
}
@Override
public int hashCode() {
return id;
}
}package kmeans;
import java.util.*;
public class Cluster {
public int id; // 簇id
public Point center; // 簇质心
public List<Point> members = new ArrayList<>(); // 簇中成员(数据集点)
public Cluster(int id, Point center) {
this.id = id;
this.center = center;
}
@Override
public boolean equals(Object o) {
if (o.getClass() != Cluster.class) {
return false;
}
return id == ((Cluster) o).id;
}
}package kmeans;
import java.util.*;
public class Kmeans {
public List<Point> samples; // 数据集点
public List<Cluster> clusters = new ArrayList<>(); // 存放聚类类簇结果
public int k; // 聚类个数
public int arr_len; // 数据集点特征维数
public int steps; // 最大迭代次数
public Kmeans(List<Point> samples, int k, int arr_len, int steps) {
this.samples = samples;
this.k = k;
this.arr_len = arr_len;
this.steps = steps;
}
public void run() {
FirstStep(); // 算法Step 1
double oldDist = Loss(); // 计算各个类簇内点到质心的距离和
double newDist = 0;
for (int i = 0; i < steps; i++) {
SecondStep(); // 算法Step 2
newDist = Loss();
if (oldDist - newDist < 0.01) { // 如果质心不再变化，则停止学习
break;
}
System.out.println("Step " + i + ":" + (oldDist - newDist));
oldDist = newDist;
}
// 打印结果
for (int i = 0; i < clusters.size(); i++) {
System.out.println("第" + i + "个簇:");
for (Point p : clusters.get(i).members) {
if (!p.isSample) {
continue;
}
System.out.print("(");
for (int xi = 0; xi < p.x.length; xi++) {
if (xi != 0) {
System.out.print(",");
}
System.out.print(p.x[xi]);
}
System.out.print(")");
System.out.println("\t" + p.text);
}
}
}
public void FirstStep() { // 算法Step 1
Set<Point> centers = new HashSet<>(); // 从样本数据集中随机选取k个不重复的质心
int id = 0; // 类簇id
while (centers.size() < k) {
Random r = new Random(); // 随机选取样本数据集的数据下标
int ti = r.nextInt(samples.size()) % samples.size();
if (centers.contains(samples.get(ti))) {
continue;
}
centers.add(samples.get(ti));
Cluster clu = new Cluster(id++, samples.get(ti));
clusters.add(clu);
}
Classify(); // 开始根据k个质心进行聚类
}
public void SecondStep() { // 算法Step 2
List<Cluster> newClusters = new ArrayList<>();
for (Cluster clu : clusters) {
double[] tx = new double[arr_len];
for (Point p : clu.members) {
for (int i = 0; i < arr_len; i++) {
tx[i] += p.x[i];
}
}
for (int i = 0; i < arr_len; i++) {
tx[i] /= clu.members.size();
} // 重新在各个类簇内部计算新的质心
Point newCenter = new Point(tx, arr_len, false, 0);
Cluster newClu = new Cluster(clu.id, newCenter);
newClusters.add(newClu);
}
clusters.clear();
clusters = newClusters;
Classify(); // 根据新的质心重新聚类
}
public void Classify() { // 聚类步骤，将各个点分配到距离最近的质心所在的类簇
for (int i = 0; i < samples.size(); i++) {
double mindistance = Double.MAX_VALUE;
int clu_Id = -1;
for (Cluster clu : clusters) {
if (samples.get(i).Distance(clu.center) < mindistance) {
mindistance = samples.get(i).Distance(clu.center);
clu_Id = clu.id;
}
}
for (int j = 0; j < clusters.size(); j++) {
if (clusters.get(j).id == clu_Id) {
clusters.get(j).members.add(samples.get(i));
break;
}
}
}
}
public double Loss() { // 计算类簇内部各个点到质心的距离
double sum = 0;
for (Cluster clu : clusters) {
for (Point p : clu.members) {
sum += p.Distance(clu.center);
}
}
return sum;
}
}package kmeans;
import java.util.*;
public class Keyven {
public static void main(String[] args) {
Scanner input = new Scanner(System.in);
int n = input.nextInt();
int arr_len = input.nextInt();
List<Point> samples = new ArrayList<>();
for (int i = 0; i < n; i++) {
double[] x = new double[arr_len];
for (int j = 0; j < arr_len; j++) {
x[j] = input.nextDouble();
}
String text = input.nextLine();
Point p = new Point(x, arr_len, true, i + 1);
p.text = text;
samples.add(p);
}
Kmeans km = new Kmeans(samples, 3, arr_len, 1000);
km.run();
input.close();
}
}实验效果
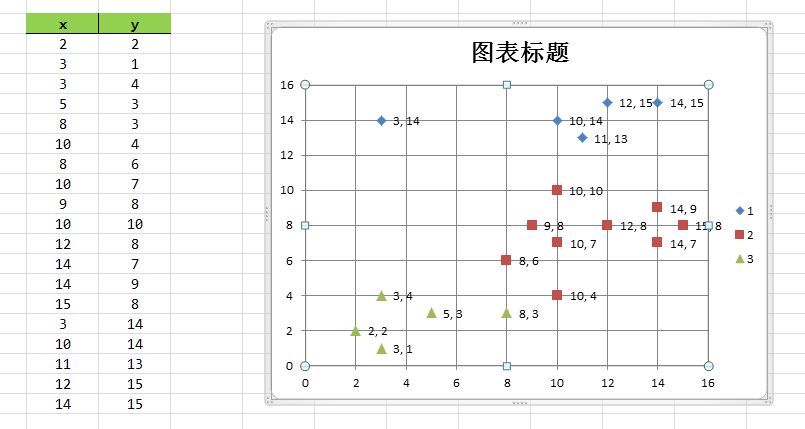
鸢尾花的数据集下载：http://archive.ics.uci.edu/ml/
算法分析
（1）离群点的处理：离群点一般称为噪音，离群点有可能影响类簇的发现，导致实验效果不合理，因此在进行Kmeans之前发现并提出离群点是有必要的。
（2）初始质心的选取：初始质心的随机选取有可能出现过度集中的情况，导致迭代次数增多，这时可以使用Kmeans++来解决这个问题，Kmeans++算法步骤如下图：
也可以使用另外一种方法：随机地选择第一个点，或取所有点的质心作为第一个点。然后，对于每个后继初始质心，选择离已经选取过的初始质心最远的点。使用这种方法，确保了选择的初始质心不仅是随机的，而且是散开的。但是，这种方法可能选中离群点。此外，求离当前初始质心集最远的点开销也非常大。
（3）算法终止条件：一般是目标函数达到最优或者达到最大的迭代次数即可终止。对于不同的距离度量，目标函数往往不同。当采用欧式距离时，目标函数一般为最小化对象到其簇质心的距离的平方和，如下：
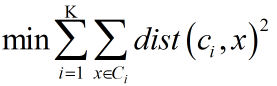
当采用余弦相似度时，目标函数一般为最大化对象到其簇质心的余弦相似度和，如下：
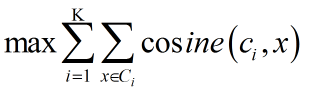
（4）K值得选取：Kmeans算法的聚类个数K 值是由用户设定的，因为一开始我们并不知道数据集的分布，Kmeans又不像EM算法那样自动学习聚类成K 个类簇。为解决这个问题，可以将Kmeans与层次聚类结合，首先采用层次聚类算法粗略决定聚类个数，并找到初始聚类，然后用Kmeans来优化聚类结果。
扩展
其它聚类算法：谱聚类、层次聚类，等。这里仅简单地介绍层次聚类、谱聚类。
1、层次聚类
层次聚类，是一种很直观的算法。顾名思义就是要一层一层地进行聚类，可以从下而上地把小的cluster合并聚集，也可以从上而下地将大的cluster进行分割，一般采用从下而上地聚类。
从下而上地合并cluster，就是每次找到距离最短的两个cluster，然后进行合并成一个大的cluster，直到全部合并为一个cluster。整个过程就是建立一个树结构，类似于下图。
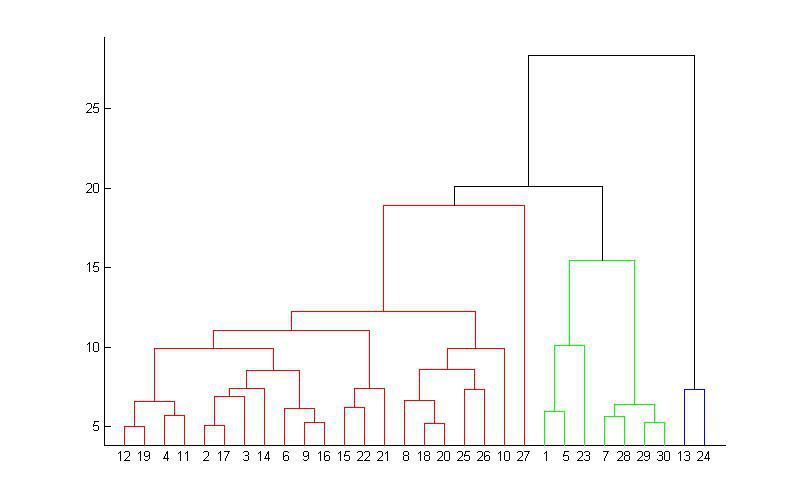
那么，如何判断两个cluster之间的距离呢？一开始每个数据点独自作为一个类，它们的距离就是这两个点之间的距离。而对于包含不止一个数据点的cluster，就可以选择多种方法了，最常用的就是average-linkage ，这种方法就是把两个集合中的点两两的距离全部放在一起求一个平均值。
只要得到了上面那样的聚类树，想要分多少个cluster都可以直接根据树结构来得到结果。
2、谱聚类
广义上来说，任何在算法中用到SVD/特征值分解的，都叫Spectral Algorithm。
传统的聚类算法，如K-Means、EM算法都是建立在凸球形样本空间上，当样本空间不为凸时，算法会陷入局部最优，最终结果受初始参数的选择影响比较大。而谱聚类可以在任意形状的样本空间上聚类，且收敛于全局最优解。
谱聚类是一种基于图论的聚类方法 。将样本看成顶点，样本的相似度看作带权边。这样，把样本集划分成K个簇的过程就等同于一个图的分割问题。将带权无向图划分为两个或两个以上的最优子图，使子图内部尽量相似，而子图间距离尽量距离较远，以达到常见的聚类的目的，其中的最优目标函数可以是割边最小分割（Smallest Cut）、也可以是分割规模差不多且割边最小的分割（Best Cut）。如下图一例：
这样，谱聚类能够识别任意形状的样本空间且收敛于全局最优解，其基本思想是利用样本数据的相似矩阵（拉普拉斯矩阵）进行特征分解后得到的特征向量进行聚类。
谱聚类算法分为3步：
构造一个N×N的权值矩阵W，Wij表示样本i 和样本j 的相似度，显然W是个对称矩阵。相似度的计算方法很多了，你可以用欧拉距离、街区距离、向量夹角、皮尔森相关系数等。并不是任意两个点间的相似度都要表示在图上，我们希望的权值图是比较稀疏的，有2种方法：权值小于阈值的认为是0；K最邻近方法，即每个点只和跟它最近的k个点连起来，CHAMELEON算法的第1阶段就是这么干的。再构造一个对角矩阵D，Dii为W第i 列元素之和。最后构造矩阵L=D-W。可以证明L是个半正定和对称矩阵。（对角矩阵是一个除主对角线之外的元素皆为 0 的矩阵。）
求L的前K小特征值对应的特征向量（这要用到奇异值分解svd了）。把K个特征向量放在一起构造一个N×K的矩阵M。
把M的每一行当成一个新的样本点，对这N个新的样本点进行K-Means聚类。
后记
注意，K-means算法与KNN算法没有关系，K-means算法是一种聚类算法，而KNN（K近邻算法）是一种分类算法，下面举一个例子来说明KNN算法。假如手头有一堆已经标记好分类的数据点集，新进来一个点，需要我们预测其类别，我们可以取该点的k 个邻居（距离该点最近的k 个点），如果这k 个邻居点大多数属于某一个类别C，则我们预测该点很大可能也属于类别C。例如下图中的黑点为预测点，取其7个邻居点，黄色居多，利用极大似然估计，我们可以认为黑色点属于黄色。
KNN算法可以使用Kd树来实现，具体请参考《统计机器学习 · 李航 著》，这里有一篇Kd-Tree的博文：Kd Tree算法原理和开源实现代码
Reference
聚类(2)——层次聚类 Hierarchical Clustering
扫一扫
1284
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
