基本原理:
克里金法用半变异函数测定空间相关要素,这里的要素是指对空间依赖的要素或者称为空间自相关要素,半变异的计算公式为:
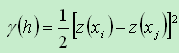
考虑“区间分组”的平均半变异计算公式
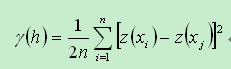
按照方向进行区间分组的方法常用的是径向扇区,ArcGIS的地统计分析模块则用格网象元进行归类。
算法的内容:
计算距离
计算协方差
网格化变异函数矩阵
沿一定方向搜索
参数:采样点,Lag(步长),方向
-
克里金法是一个占用大量处理器资源的过程。执行速度取决于输入数据集中点的数量和搜索窗口的大小。
-
预测栅格可选输出方差中的低值指示预测值的高置信度。值较高,可能表明需要使用更多的数据点。
-
泛克里金法类型假定有结构组件存在,且局部趋势将随位置的变化而变化。
-
高级参数可控制克里金法所使用的半变异函数。步长大小的默认值初始设置为默认输出像元大小。对于主要范围、偏基台和块金来说,如果未进行任何设置,将会内部计算默认值。
-
预测栅格的可选输出方差在每个输出栅格像元中都含有克里金法方差。假设克里金误差是正态分布的,则像元中实际 z 值等于预测栅格值加上或减去预测栅格中值的平方根 2 倍的可能性为 95.5%。
























 549
549

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








