并查集

并查集

并查集是对树的一种操作，旨在找到某个节点的公共祖先（最老公共祖先）。我们先讲一下并。

并

并就是讲两个节点合并到一个集合里面（这个集合必须是树），每个节点对应一个祖先，最老公共祖先的祖先就是自己，而每个节点在合并前的初始值也是自己，也就是：若有一个节点 a ,设它的祖先为 f[a] ,那么它的初始值就是 f[a]=a ,。这个合并操作并不难，只要判断一下这两个节点是否有祖先，没有就很好办，直接随便连，比如： a 和 b ，他们都没有祖先（也就是祖先是自己），那么就可以 f[a]=b，如果 f[a]≠a 那么就让 b 的最老祖先（可能是自己）再往上多一个祖先 f[a]，此时 b 的最老祖先也就是 aa 的最老祖先了（不一定是 a ）。具体算法如下：

void unionn(int p,int q,int bj)
{
  int t,p1,q1;
  p1=find(p);//搜索p的祖先
  q1=find(q);//搜索q的祖先
  if(p1==q1) return;//祖先都相同了，退出
  t=father[p1]+father[q1];//两个集合的总人数，因为初始化时father[]全部都等于-1，利用abs求的集合的人数
  if(father[p1]>father[q1]) {father[p1]=q1;father[q1]=t;}
  else{father[q1]=p1;father[p1]=t;}
  //哪边人数多就令另外一边的祖先指向人数多的一边
}

查

有时候我们需要查某个节点的最老祖先是谁，主要是为了下面判断某两个节点的最老祖先是否相同而准备的。假如有这样一组关系：

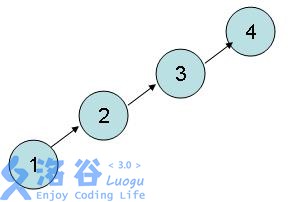
比如我们要找 11 的最老祖先，那么怎么找呢？那么就要通过 33 来找，再往上找，这样的话代码就是：

int find(int f[], int x) 
{
    if(f[x]>0)return x;//如果是祖先，就返回最老祖先的值
    return find(f[x]);//不是最老祖先，那么就往上继续找
}

但是，这样做的话，会有很多重复工作。比如我刚才找 11 ，现在找 22 ，那么你就重复搜索了 22 。此时我们就需要压缩路径，以便后面查找时更便捷。压缩路径的话，就是在查找的时候，顺带把经过的节点的祖先直接指向最老祖先，那么后面找最老祖先的时候，就一步到位了。代码如下：

int find(int x) 
{
    if(f[x]>0)return x;//如果是祖先，就返回最老祖先的值
    return f[x]=find(f[x]);//不是最老祖先，那么就往上继续找,并令当前的x直接指向祖先，压缩路径
}

线性写法：

int find(int p)
{
 int i,j;
 i=p;
 while(father[i]>=0) i=father[i];//不是最老祖先，那么就往上继续找
 while(i!=p)
 {
  j=father[p];
  father[p]=i;
  p=j;
 }//将路径上的所有点全部指向祖先
return i;
}

这种方法十分巧妙，压缩路径之后，查找的速度也会快得多。

总结完毕，谢谢

转载于:https://www.cnblogs.com/kurlisjoey/p/10880721.html