季节性分解

2019独角兽企业重金招聘Python工程师标准>>>

• 季节性因素的时间序列

存在季节性因素的时间序列（如月度数据、季度数据）可被分解为趋势因子、季节性因子、随机性因子

趋势因子(trend componnet)：能捕捉到长期变化；

季节性因子(seasonal componnet)：能捕捉到一年内的周期性变化；

随机（误差）因子：(irregular/error component)：捕捉到哪些不能被趋势或季节效应解释的变化

• 加法模型

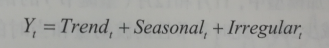
 其中 时刻 t 的观测值即这一时刻的趋势值、季节效应以及随机影响之和

• 乘法模型

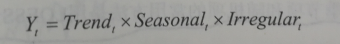
 即趋势项、季节项和随机影响相乘

• 将时序做分解

将时序分解为趋势项、季节项和随机项常用的方法用LOESS光滑做季节性分解，可以通过R中的 stl() 函数

stl(ts, s.window = , t.window = ,)

ts（必填）：将要分解的时序

s.window（必填） ：控制季节效应变化的速度，较小的值意味着更快的变化速度， 令 s.window = "periodic"可使得季节效应在各年间都一样

t.window：控制趋势项变化的速度

更多的细节查看help(stl)

虽然stl()函数只能处理相加模型，相乘模型总可以通过对数变换转换成相加模型：

  用经过对数变换的序列拟合出的相加模型也总可以再转化回原始尺度

#使用R中自带的 AirPssengers序列描述1949-1960每个月国际航班的乘客
> plot(AirPassengers) #画出序列
> lAirPassengers <- log(AirPassengers)  #对其进行对数变换
> plot(lAirPassengers,ylab="log(AirPassengers)")
> fit <- stl(lAirPassengers,s.window = "period")#进行分解 ，如下图1
> plot(fit)  #绘制分解后的图
> fit$time.series  #time.series，它包括每个观测值中的趋势、季节以及随机效应，直接使用fit$time.series返回对数变换后的时序，通过exp(fit$time.series)可将结果转化为原始尺度
            seasonal    trend     remainder
Jan 1949 -0.09164042 4.829389 -0.0192493585
Feb 1949 -0.11402828 4.830368  0.0543447685
Mar 1949  0.01586585 4.831348  0.0355884457
Apr 1949 -0.01402759 4.833377  0.0404632511
May 1949 -0.01502478 4.835406 -0.0245905300
Jun 1949  0.10978976 4.838166 -0.0426814256
Jul 1949  0.21640041 4.840927 -0.0601151688
Aug 1949  0.20960587 4.843469 -0.0558624690
Sep 1949  0.06747156 4.846011 -0.0008273977
Oct 1949 -0.07024836 4.850883 -0.0015112948
Nov 1949 -0.21352774 4.855756  0.0021630667
Dec 1949 -0.10063625 4.864586  0.0067346600
Jan 1950 -0.09164042 4.873417 -0.0368443057
Feb 1950 -0.11402828 4.883282  0.0670284530
Mar 1950  0.01586585 4.893147  0.0397474219
Apr 1950 -0.01402759 4.903156  0.016145995