米哈游（原神）一面算法原题

世界线收缩

上一次发「米哈游（原神）」算法原题的日期是 08-26，今天再发，本来仅仅是因为有新的读者投稿（新题）。

但在我回顾上一次「米哈游（原神）」算法原题的 帖子 时，发现了很有意思的东西。

当时的唠嗑内容，是极越公关负责人喷小米汽车，而又光速道歉的事儿：

再结合昨天的 帖子 中某位同学的留言评论，有种恍如隔世的感觉。

小米汽车已经突破了一定的产能问题，有稳定的销量，还推出了新的车型，一个是已经开放预订的性能轿车「SU7 Ultra」，以及刚刚亮相不久的首款 SUV 车型「YU 7」。

而极越汽车，最近刚刚倒闭，社保和公积金都被曝拖欠，办公室的微波炉也被顺走了。

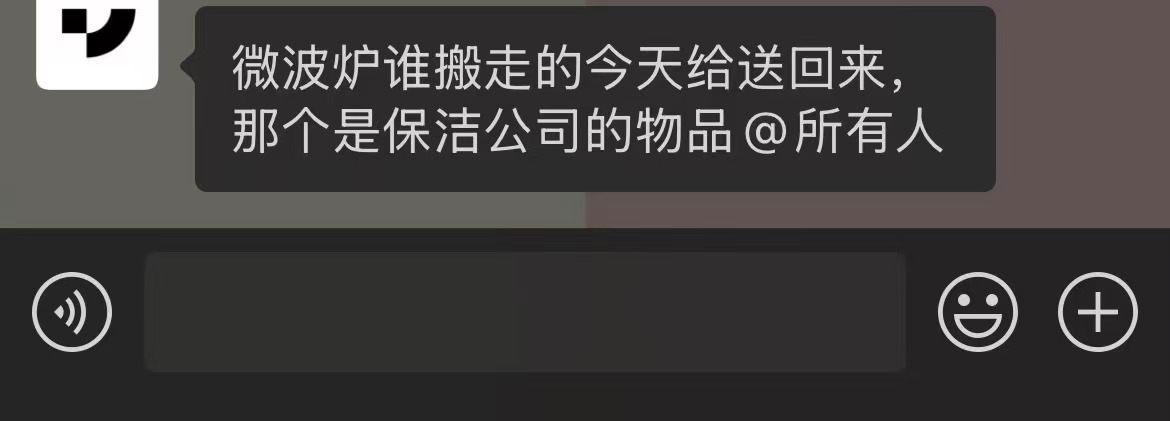
如果说这一切和"米哈游"能有啥关系的话，除了帮我们串起两件事儿以外，还有一句游戏领域的名言，可以用来解释「小米」和「极越」之间的差异，就是 菜是原罪 。

产品力也好，性价比也罢，最终都要转化为具体的销量，企业才有下一步。

向极越一般，光靠在发布会大谈数字，给产品加一些在自己看来是创新，在用户看来全是槽点的设计，走向该结局，并不意外。

...

回归主题。

来一道和「米哈游（原神）」一面相关的算法题。

题目描述

平台：LeetCode

题号：1537

你有两个 有序 且数组内元素互不相同的数组 nums1 和 nums2 。

一条 合法路径 定义如下：

• 选择数组 nums1 或者 nums2 开始遍历（从下标 处开始）。
• 从左到右遍历当前数组。
• 如果你遇到了 nums1 和 nums2 中都存在的值，那么你可以切换路径到另一个数组对应数字处继续遍历（但在合法路径中重复数字只会被统计一次）。

得分定义为合法路径中不同数字的和。

请你返回所有可能合法路径中的最大得分。

由于答案可能很大，请你将它对 取余后返回。

示例 1：

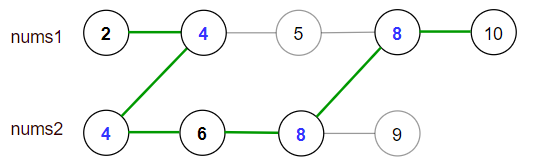
输入：nums1 = [2,4,5,8,10], nums2 = [4,6,8,9]

输出：30

解释：合法路径包括：
[2,4,5,8,10], [2,4,5,8,9], [2,4,6,8,9], [2,4,6,8,10],（从 nums1 开始遍历）
[4,6,8,9], [4,5,8,10], [4,5,8,9], [4,6,8,10]  （从 nums2 开始遍历）
最大得分为上图中的绿色路径 [2,4,6,8,10] 。

示例 2：

输入：nums1 = [1,3,5,7,9], nums2 = [3,5,100]

输出：109

解释：最大得分由路径 [1,3,5,100] 得到。

示例 3：

输入：nums1 = [1,2,3,4,5], nums2 = [6,7,8,9,10]

输出：40

解释：nums1 和 nums2 之间无相同数字。
最大得分由路径 [6,7,8,9,10] 得到。

示例 4：

输入：nums1 = [1,4,5,8,9,11,19], nums2 = [2,3,4,11,12]

输出：61

提示：

• nums1 和  nums2 都是严格递增的数组。

前缀和 + 构造（分段计算）

一个简单且正确的做法，是我们构造一种决策方案，使得能够直接计算出最大得分。

首先，在最佳路径中所有的公共点都必然会经过，因此我们可以将值相等的点进行合并，即看作同一个点。

利用两个数组均满足「单调递增」，我们可以通过 的复杂度统计出那些公共点，以二元组 的形式存储到 list 数组（二元组含义为 ）。

对于 list 中的每对相邻元素（相邻公共点），假设为 和 ，我们可以通过「前缀和」计算出 以及 的和，从而决策出在 （或者说是 ，这两个是同一个点）时，我们应当走哪一段。

当计算完所有公共点之间的得分后，对于最佳路线的首位两端，也是结合「前缀和」做同样的逻辑处理即可。

Java 代码：

class Solution {
    int MOD = (int)1e9 + 7;
    public int maxSum(int[] nums1, int[] nums2) {
        int n = nums1.length, m = nums2.length;
        long[] s1 = new long[n + 10], s2 = new long[m + 10];
        for (int i = 1; i <= n; i++) s1[i] = s1[i - 1] + nums1[i - 1];
        for (int i = 1; i <= m; i++) s2[i] = s2[i - 1] + nums2[i - 1];
        List<int[]> list = new ArrayList<>();
        for (int i = 0, j = 0; i < n && j < m; ) {
            if (nums1[i] == nums2[j]) list.add(new int[]{i, j});
            if (nums1[i] < nums2[j]) i++;
            else j++;
        }
        long ans = 0;
        for (int i = 0, p1 = -1, p2 = -1; i <= list.size(); i++) {
            int idx1 = 0, idx2 = 0;
            if (i < list.size()) {
                int[] info = list.get(i);
                idx1 = info[0]; idx2 = info[1];
            } else {
                idx1 = n - 1; idx2 = m - 1;
            }
            long t1 = s1[idx1 + 1] - s1[p1 + 1], t2 = s2[idx2 + 1] - s2[p2 + 1];
            ans += Math.max(t1, t2);
            p1 = idx1; p2 = idx2;
        }
        return (int)(ans % MOD);
    }
}

C++ 代码：

class Solution {
public:
    const int MOD = 1e9 + 7;
    int maxSum(vector<int>& nums1, vector<int>& nums2) {
        int n = nums1.size(), m = nums2.size();
        vector<long long> s1(n + 10), s2(m + 10);
        for (int i = 1; i <= n; i++) s1[i] = s1[i - 1] + nums1[i - 1];
        for (int i = 1; i <= m; i++) s2[i] = s2[i - 1] + nums2[i - 1];
        vector<pair<int, int>> list;
        for (int i = 0, j = 0; i < n && j < m; ) {
            if (nums1[i] == nums2[j]) list.emplace_back(i, j);
            if (nums1[i] < nums2[j]) i++;
            else j++;
        }
        long long ans = 0;
        for (int i = 0, p1 = -1, p2 = -1; i <= list.size(); i++) {
            int idx1 = 0, idx2 = 0;
            if (i < list.size()) {
                auto [info1, info2] = list[i];
                idx1 = info1; idx2 = info2;
            } else {
                idx1 = n - 1; idx2 = m - 1;
            }
            long long t1 = s1[idx1 + 1] - s1[p1 + 1], t2 = s2[idx2 + 1] - s2[p2 + 1];
            ans += max(t1, t2);
            p1 = idx1; p2 = idx2;
        }
        return ans % MOD;
    }
};

• 时间复杂度：
• 空间复杂度：

序列 DP

另外一个较为常见的做法是「序列 DP」做法。

定义 代表在 nums1 上进行移动，到达 的最大得分；定义 代表在 nums2 上进行移动，到达 的最大得分。

由于两者的分析是类似的，我们以 为例进行分析即可。

不失一般性考虑 如何转移，假设当前处理到的是 ，根据 是否为公共点，进行分情况讨论：

• 不为公共点，此时只能由 转移而来，即有 ；
• 为公共点（假设与 公共），此时能够从 或 转移而来，我们需要取 和 的最大值，即有 。

更重要的是，我们需要确保计算 时， 已被计算完成。

由于最佳路线必然满足「单调递增」，因此我们可以使用「双指针」来对 和 同时进行转移，每次取值小的进行更新，从而确保更新过程也是单调的，即当需要计算 时，比 小的 和 均被转移完成。

Java 代码：

class Solution {
    int MOD = (int)1e9 + 7;
    public int maxSum(int[] nums1, int[] nums2) {
        int n = nums1.length, m = nums2.length;
        long[] f = new long[n + 1], g = new long[m + 1];
        int i = 1, j = 1;
        while (i <= n || j <= m) {
            if (i <= n && j <= m) {
                if (nums1[i - 1] < nums2[j - 1]) {
                    f[i] = f[i - 1] + nums1[i - 1];
                    i++;
                } else if (nums2[j - 1] < nums1[i - 1]) {
                    g[j] = g[j - 1] + nums2[j - 1];
                    j++;
                } else {
                    f[i] = g[j] = Math.max(f[i - 1], g[j - 1]) + nums1[i - 1];
                    i++; j++;
                }
            } else if (i <= n) {
                f[i] = f[i - 1] + nums1[i - 1];
                i++;
            } else {
                g[j] = g[j - 1] + nums2[j - 1];
                j++;
            }
        }
        return (int) (Math.max(f[n], g[m]) % MOD);
    }
}

C++ 代码：

class Solution {
public:
    const int MOD = 1e9 + 7;
    int maxSum(vector<int>& nums1, vector<int>& nums2) {
        int n = nums1.size(), m = nums2.size();
        vector<long long> f(n + 1, 0), g(m + 1, 0);
        int i = 1, j = 1;
        while (i <= n || j <= m) {
            if (i <= n && j <= m) {
                if (nums1[i - 1] < nums2[j - 1]) {
                    f[i] = f[i - 1] + nums1[i - 1];
                    i++;
                } else if (nums2[j - 1] < nums1[i - 1]) {
                    g[j] = g[j - 1] + nums2[j - 1];
                    j++;
                } else {
                    f[i] = g[j] = max(f[i - 1], g[j - 1]) + nums1[i - 1];
                    i++; j++;
                }
            } else if (i <= n) {
                f[i] = f[i - 1] + nums1[i - 1];
                i++;
            } else {
                g[j] = g[j - 1] + nums2[j - 1];
                j++;
            }
        }
        return max(f[n], g[m]) % MOD;
    }
};

• 时间复杂度：
• 空间复杂度：

最后

巨划算的 LeetCode 会员优惠通道目前仍可用 ~

使用福利优惠通道 leetcode.cn/premium/?promoChannel=acoier，年度会员 有效期额外增加两个月，季度会员 有效期额外增加两周，更有超大额专属 🧧 和实物 🎁 福利每月发放。

我是宫水三叶，每天都会分享算法知识，并和大家聊聊近期的所见所闻。

欢迎关注，明天见。

更多更全更热门的「笔试/面试」相关资料可访问排版精美的 合集新基地 🎉🎉