MATLAB RLC电路状态响应仿真项目

谢兴豪

于 2025-06-16 16:48:37 发布

阅读量859

点赞数 9

CC 4.0 BY-SA版权

本文链接：https://blog.youkuaiyun.com/weixin_32661831/article/details/148703660

本文还有配套的精品资源，点击获取

简介：本项目介绍了一个电子工程与计算机编程结合的仿真案例，专注于RLC电路理论基础及其在MATLAB中的状态响应分析。项目涉及RLC电路模型的建立，状态空间模型的构建，以及使用MATLAB脚本文件进行电路参数定义、初始条件设定、状态方程求解和状态响应曲线绘制。通过这些仿真活动，工程师和研究人员可以加深对电路滤波特性、谐振频率和稳定性等特性的理解，同时也提供了如何使用编程解决复杂电路问题的实践案例。 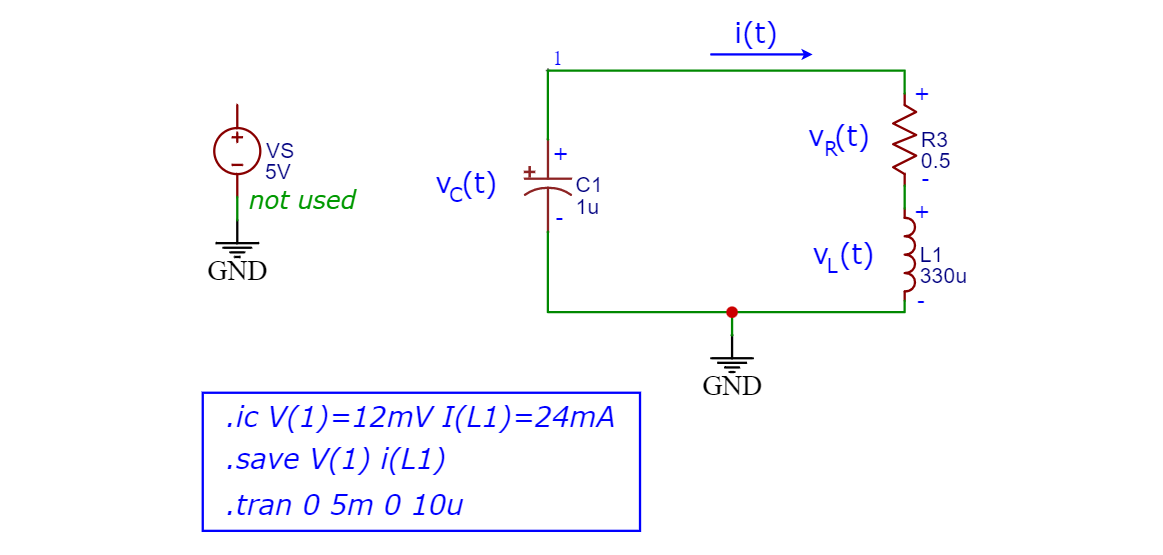RLC电路仿真

1. RLC电路理论基础

在本章中，我们将首先深入探讨RLC电路的理论基础，包括电路元件电阻（R）、电感（L）和电容（C）的基本概念及其特性。这些基础元件是构成复杂电路的基石，了解它们的特性对于分析和设计电子系统至关重要。

1.1 RLC电路的数学描述

电阻（R）是电路中阻碍电流流动的元件，其数学描述通常为欧姆定律（V=IR）。电感（L）存储能量于磁场中，其特性表现为通过其电流变化率的反作用，数学上由电感方程（V=L*di/dt）描述。电容（C）则储存能量于电场中，其特性表现为电压与存储的电荷量成正比，数学上由电容方程（V=Q/C）表达。

1.2 RLC电路的动态特性

RLC电路的动态特性涉及到电路如何响应外部激励。在交流（AC）电路中，电阻、电感和电容的组合决定了电路的阻抗特性。电感和电容的相互作用会产生谐振现象，这在许多电子系统中都有广泛应用，如滤波器和振荡器的设计。

通过上述分析，我们可以得出，RLC电路作为电子电路中最基本的模块，其理论知识是我们深入研究电路系统复杂行为的基石。下一章我们将介绍如何使用MATLAB工具来构建这些理论模型的状态空间表示，进而分析和设计复杂的电子系统。

2. MATLAB状态空间模型构建

2.1 状态空间表达式的引入

2.1.1 状态空间模型概念

在控制理论中，状态空间模型是描述线性系统动态行为的一种数学方法。该模型使用一组一阶微分方程来表示系统的所有动态状态，这些状态变量描述了系统的内部条件。状态空间模型不仅适用于连续时间系统，也适用于离散时间系统。

对于RLC电路而言，状态空间模型允许我们利用现代控制理论的方法来进行分析和设计。电路的状态变量通常包括电容器上的电压和电感器上的电流，它们能够完全描述电路的动态行为。

2.1.2 状态空间模型与RLC电路关系

在RLC电路中，状态空间模型的构建可以帮助我们深入理解电路的稳定性、可控性和可观测性。通过定义状态变量、输入、输出和系统的内部结构，我们可以将复杂的电路方程转化为易于计算机仿真的形式。

构建状态空间模型的步骤包括：选取合适的状态变量，建立状态方程和输出方程，然后通过矩阵形式表示它们。对于一个给定的RLC电路，状态空间模型可以被用来分析电路的自然响应和强迫响应。

2.2 状态空间模型构建方法

2.2.1 线性系统状态方程推导

对于一个线性时不变（LTI）系统，如RLC电路，状态方程可以表示为：

dx/dt = Ax(t) + Bu(t)
y(t) = Cx(t) + Du(t)

其中， x(t) 是状态向量， u(t) 是输入向量， y(t) 是输出向量， A 、 B 、 C 和 D 是系统的矩阵，它们分别代表了系统动态、输入增益、输出增益和直接传递矩阵。

在RLC电路的情况下，状态向量可以是电容器电压和电感器电流的集合，而系统矩阵 A 、 B 、 C 和 D 则可以根据电路的拓扑结构和元件参数来确定。

2.2.2 状态矩阵A、B、C和D的确定

为了构建RLC电路的状态空间模型，我们需要根据电路的方程推导出矩阵 A 、 B 、 C 和 D 的具体值。

A 矩阵（系统矩阵）定义了状态变量随时间的变化率。
B 矩阵（输入矩阵）表示输入如何影响系统的状态变量。
C 矩阵（输出矩阵）定义了状态变量与系统输出之间的关系。
D 矩阵（直接传递矩阵）表示输入对输出的直接影响。

这些矩阵可以通过电路方程使用基尔霍夫定律得出，即应用电压和电流定律来构建矩阵方程。

为了演示这一过程，以下是一个简单RLC电路的状态空间表示的代码实现示例。

% 假设电路参数为：R=1欧姆，L=0.5亨利，C=0.2法拉
R = 1;
L = 0.5;
C = 0.2;

% 定义矩阵A，B，C和D
A = [0, 1/L; -1/(R*C), -1/(R*C)];
B = [0; 1/C];
C = [1, 0];
D = [0];

% 系统矩阵A，B，C和D现在已准备好
% 状态空间模型可以使用这些矩阵在MATLAB中构建

在这个例子中，我们假设一个RLC串联电路，其中 R 、 L 和 C 分别为电阻、电感和电容的值。通过应用电路的基本定律，我们能够推导出相应的状态空间模型矩阵。

构建状态空间模型是电路分析和控制系统设计的关键步骤。通过MATLAB，可以轻松地进行复杂的计算，并且能够快速验证和模拟电路的行为。在下一节，我们将进一步详细地探讨状态方程求解和状态响应曲线的绘制。

3. RLC电路参数定义与初始条件设置

3.1 RLC电路参数的数学描述

3.1.1 电阻(R)、电感(L)、电容(C)的参数定义

在RLC电路中，电阻(R)、电感(L)、电容(C)是构成电路的基础元件，它们各自具有特定的数学描述和物理含义。电阻代表了电路元件对电流流动的阻碍作用，其值越大，阻碍作用越强。数学上，电阻的单位是欧姆(Ω)，其电阻值可以通过公式 ( R = \rho \frac{L}{A} ) 计算得到，其中 ( \rho ) 是材料的电阻率，( L ) 是电阻元件的长度，( A ) 是横截面积。

电感(L)是电路元件中产生磁场的能力的度量，电感越大，电路产生的磁场也越强。电感的单位是亨利(H)，其值通常由线圈的匝数、线圈的几何尺寸以及线圈中磁芯的材料属性决定。电感的数学表达式为 ( L = \frac{N^2}{R_m} )，其中 ( N ) 是线圈的匝数，( R_m ) 是磁芯材料的磁阻。

电容(C)则是衡量电路元件储存电荷能力的指标，电容越大，储存的电荷量越多。其单位为法拉(F)，数学表达式为 ( C = \frac{A\epsilon}{d} )，其中 ( A ) 是两极板的面积，( \epsilon ) 是介质的介电常数，( d ) 是极板间的距离。

3.1.2 参数对电路动态特性的影响

电阻、电感和电容参数对电路的动态特性有重大影响。电阻影响电路中的能量消耗，电感和电容影响电路中能量的存储和释放。具体来说：

电阻可以限制电流的大小，根据欧姆定律 ( I = \frac{V}{R} )，电路中的电流与电阻成反比。
电感对电流变化起阻抗作用，产生反电动势，根据法拉第电磁感应定律 ( e = -L \frac{dI}{dt} )，电感会产生一个与电流变化率成正比的电动势。
电容能够储存电荷，允许电流流过，但阻止电压突变，根据 ( I = C \frac{dV}{dt} )，电容会对电压变化产生反应。

在RLC电路的交流分析中，电阻、电感和电容将决定电路的阻抗特性，并影响电路的谐振频率和品质因数。

3.2 初始条件的设定与重要性

3.2.1 初始电荷、电流的确定

在RLC电路的仿真和实际应用中，电路初始状态的设定对于电路行为的预测至关重要。初始条件通常包括电路初始时刻的电荷和电流值。对于电容元件，初始电荷 ( Q_0 ) 可以通过其初始电压 ( V_0 ) 和电容量 ( C ) 的关系 ( Q_0 = CV_0 ) 来确定。对于电感元件，初始电流 ( I_0 ) 则直接决定了电路的初始能量存储情况。

在MATLAB中，设定初始条件可以通过以下代码实现：

% 设定初始条件
initial_state = [Q0; I0]; % Q0是电容初始电荷，I0是电感初始电流

3.2.2 初始条件对仿真结果的影响

初始条件在电路分析中的重要性在于它能够决定电路在动态过程开始时的状态。没有正确的初始条件，电路的仿真可能无法准确反映真实的电路行为。例如，在RLC串联电路中，如果忽略了初始电流，可能导致仿真过程中电流瞬变的错误模拟。

初始条件的影响可以通过解耦微分方程来分析。电路的动态行为由状态方程描述，状态方程通常是一组线性微分方程，其解依赖于初始条件。因此，初始电荷和电流的设定直接影响微分方程的解，进而影响电路的响应。

在MATLAB中，使用ode45等数值求解函数求解电路的状态方程时，初始条件作为函数参数直接提供，例如：

% 使用ode45函数求解电路状态方程
[t, states] = ode45(@(t, y) state_space_equation(t, y, ...), tspan, initial_state);

在上述代码中， initial_state 向量中包含了初始电荷和电流信息，它被传递给了求解器函数 ode45 ，以确保电路的初始状态被正确设置。

4. 状态方程求解与状态响应曲线绘制

4.1 利用MATLAB求解状态方程

4.1.1 状态方程的数值解法介绍

在RLC电路分析中，状态方程提供了电路行为的数学描述。这些方程通常是非线性的，解析解难以直接获得，因此数值方法被广泛应用于求解状态方程。数值方法能够处理复杂的非线性问题，并且能够提供在特定时间点上的近似解。MATLAB提供了多种数值解法函数，其中ode系列函数是最为强大的工具。

ode系列函数能够求解形式如下的初值问题：

[ \begin{align } \frac{dx(t)}{dt} &= f(t, x(t)), \quad t \geq t_0, \ x(t_0) &= x_0, \end{align } ]

其中(x(t))表示系统在时间(t)的状态，(f(t, x(t)))是一个向量函数，表示系统状态随时间变化的率。

4.1.2 MATLAB函数ode45的使用

ode45是MATLAB中用于求解常微分方程初值问题的函数之一，它基于四阶和五阶Runge-Kutta方法。ode45适合求解非刚性问题，并且能够自动适应步长以保证计算的准确性。

ode45函数的基本使用格式如下：

[t, x] = ode45(@odefun, tspan, x0);

odefun ：函数句柄，该函数定义了状态方程，即(f(t, x(t)))。
tspan ：求解的时间跨度，形式为 [t0, tf] ，其中 t0 是初始时间点， tf 是最终时间点。
x0 ：初始状态向量。
t ：返回的时间向量，其中包含了求解时间点。
x ：返回的状态矩阵，每列对应一个时间点的状态向量。

接下来，我们将通过一个具体的RLC电路状态方程的求解案例来展示ode45函数的使用。

4.2 状态响应曲线的绘制技巧

4.2.1 响应曲线的类型与特征

状态响应曲线是指状态变量随时间变化的曲线图。在RLC电路分析中，这些曲线帮助我们理解电路在不同初始条件下的动态行为。根据电路的输入激励和电路类型，状态响应曲线通常分为以下几种类型：

自由响应：电路在没有外部输入激励下的自然行为，包括瞬态响应和稳态响应。
强迫响应：电路在外部输入激励作用下的行为。
全响应：电路在自由响应和强迫响应叠加后的总行为。

每种类型的响应曲线都有其特定的特征。例如，自由响应中，电路的振荡频率和阻尼比可以反映电路参数特性。

4.2.2 利用MATLAB绘图函数绘制响应曲线

MATLAB提供了强大的绘图功能，可以快速地绘制各种响应曲线。使用plot函数，可以轻松地将计算得到的状态变量随时间的变化绘制出来。

plot(t, x);
xlabel('Time (s)');
ylabel('States');
title('State Response Curves');
grid on;

此外，MATLAB还提供了如 semilogx 、 semilogy 、 loglog 等函数，用于绘制不同坐标轴上的曲线，适合于需要特殊坐标轴表示的响应曲线。

在绘制曲线时，我们还可以通过添加图例、更改线型和颜色等方式，来提高曲线图的可读性和美观度。

绘制响应曲线是分析电路动态特性的关键步骤，通过MATLAB，可以有效地将数值计算结果转化为直观的图形，帮助工程师快速理解电路的行为特性。在下一小节中，我们将通过具体实例演示如何绘制RLC电路的响应曲线。

5. 滤波器设计、信号处理与理论实践结合

5.1 滤波器与信号处理器设计基础

在RLC电路中，滤波器设计是至关重要的，它决定了电路对特定频率信号的传输或抑制能力。滤波器的设计基于一系列的数学原理和理论。

5.1.1 滤波器设计的基本原理

滤波器根据其设计目标可以分为低通、高通、带通和带阻几种类型。每种类型的滤波器都有其特定的频率响应，从而允许或抑制不同频率的信号。

低通滤波器（LPF） ：允许低频信号通过，阻止高频信号。
高通滤波器（HPF） ：允许高频信号通过，阻止低频信号。
带通滤波器（BPF） ：允许一定频率范围内的信号通过，其他频率范围的信号被阻止。
带阻滤波器（BRF）或陷波器（Notch） ：阻止一个特定频率范围的信号，而允许其它频率的信号通过。

滤波器设计主要涉及以下两个方面： - 电路设计 ：包括电阻、电容、电感等元件的选择与配置。 - 数学模型 ：例如巴特沃斯、切比雪夫、贝塞尔等滤波器原型的传递函数。

5.1.2 信号处理器在RLC电路中的应用

信号处理器在RLC电路中起到了不可或缺的作用。现代信号处理器不仅能够处理模拟信号，也能够对数字信号进行处理。

模拟信号处理器 ：在模拟电路中对信号进行放大、滤波、调制等操作。
数字信号处理器 ：在数字领域，通过算法对信号进行分析、转换、存储等操作。

信号处理器的应用极大地提升了RLC电路的性能和灵活性，例如在无线通信系统中，信号处理器可以实现信号的调制、解调、滤波等多种功能。

5.2 常用MATLAB函数在RLC仿真中的应用

在RLC电路仿真中，MATLAB提供了丰富的函数库，这些函数可以帮助我们快速实现复杂的信号处理和电路仿真。

5.2.1 findx0.m初始值函数的使用

findx0.m 是一个专门用于寻找系统初始状态的MATLAB函数。这个函数对于状态空间模型的仿真尤为重要，因为它需要一个初始状态向量作为输入。函数的使用方法如下：

% 假设我们有状态方程的A、B、C、D矩阵
A = [...]; B = [...]; C = [...]; D = [...];
% 使用findx0.m来获取初始状态x0
x0 = findx0(A, B, C, D, U0, Y0);
% 其中U0是初始输入，Y0是初始输出

findx0 函数基于给定的初始输入 U0 和初始输出 Y0 ，求解线性方程组来找到一个可能的初始状态 x0 ，它允许仿真从正确的初始条件开始。

5.2.2 其他仿真相关函数介绍

MATLAB还提供了其他许多有用的功能，例如：

lqr ：线性二次调节器设计，用于控制理论中的优化问题。
tf ：从传递函数或零极点增益表示创建传递函数模型。
step ：绘制系统的阶跃响应，评估系统性能。

这些函数通常用于设计控制器、分析系统响应以及优化电路性能。

5.3 理论与实践的结合

5.3.1 理论知识在仿真中的应用分析

将理论知识应用到仿真实践中是理解电路行为和提高设计性能的关键。RLC电路的理论基础能够帮助我们预测电路在不同条件下的表现。

比如，一个低通滤波器的设计需要我们应用RLC电路的阻抗计算方法和滤波器设计理论来确定合适的元件值。

5.3.2 实际案例讨论：理论指导下的RLC电路设计与优化

举一个实际案例，假设我们要设计一个应用于无线通信系统中的带通滤波器。在设计开始之前，需要决定滤波器的中心频率和带宽，并根据设计参数计算出电阻、电容、电感的值。

设计完成后，我们可以使用MATLAB中的仿真工具来验证理论设计的准确性。比如，通过使用 filterDesigner 工具箱来模拟滤波器的频率响应，并且使用 ode45 来分析电路对不同信号的时域响应。

% 定义RLC电路的参数
R = 10; L = 1e-3; C = 1e-6;
% 定义初始状态
x0 = [0; 0]; % 假设初始电流和电压都是0
% 定义仿真时间
tspan = [0, 0.01];

% 使用ode45求解电路的状态响应
[t, y] = ode45(@(t, y) rlcEquations(t, y, R, L, C), tspan, x0);

% 绘制电流随时间变化的响应曲线
figure;
plot(t, y(:, 1));
title('电流随时间变化的响应曲线');
xlabel('时间 (s)');
ylabel('电流 (A)');

其中 rlcEquations 是一个自定义函数，它根据RLC电路的状态空间模型来计算电路在任意时间点的状态。

通过上述仿真过程，我们可以验证设计是否满足性能要求，并进行必要的调整。这种理论与实践的结合不仅加深了对RLC电路的理解，还提高了我们设计和优化电路的能力。

本文还有配套的精品资源，点击获取