简介:Kohonen自组织映射(SOM)是一种无监督学习算法,擅长于数据降维和可视化。本文详细介绍了如何使用Python及其 minisom 库来实现SOM算法,包括安装库、数据准备、初始化网络、训练过程、数据映射及结果可视化等步骤。SOM还可用于聚类分析、异常检测等,该项目中包含代码示例和数据集,有助于深入理解SOM的工作原理和实现细节。 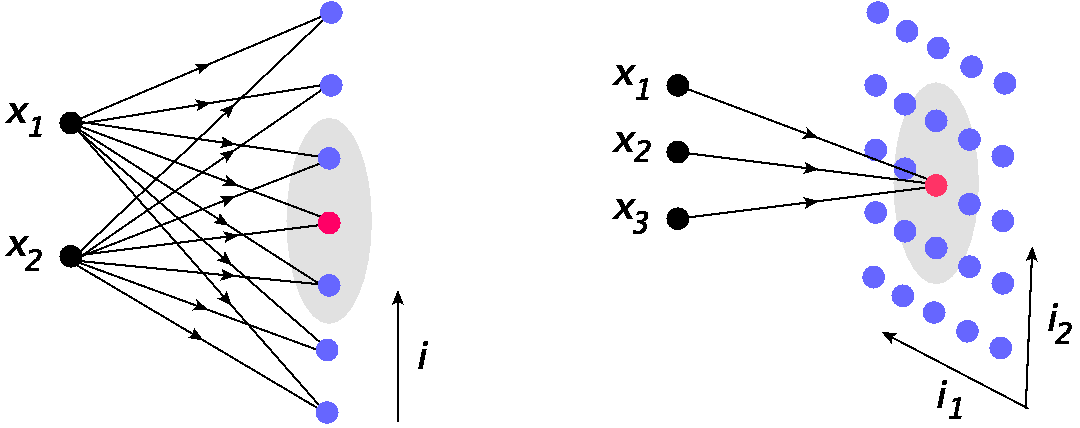
1. Kohonen自组织映射简介
自组织映射(Self-Organizing Map,SOM),是由芬兰学者Teuvo Kohonen在1981年提出的,旨在模拟人脑中无监督学习的神经网络模型。SOM网络以一种竞争学习的方式实现特征的抽取和数据的可视化,因此在很多领域,如模式识别、数据可视化和聚类分析中有着广泛的应用。
在本章中,我们将介绍SOM的理论背景和基础概念。我们首先会探讨SOM的工作原理,说明它是如何将高维数据映射到低维空间的。然后,通过与其他类型的人工神经网络对比,突出SOM的独特之处。通过这一章节的学习,读者将能够对SOM有一个初步的认识,为其后章节中在Python环境下实现和应用SOM奠定基础。
2. Python实现SOM的基础步骤
2.1 SOM理论基础
2.1.1 自组织映射的工作原理
自组织映射(Self-Organizing Map,SOM),也称作Kohonen网络,是一种无监督学习算法,常用于数据可视化、聚类分析等领域。它的基本原理是将高维数据映射到低维空间(通常是二维格子)上,并保持数据的拓扑结构,从而使得具有相似特性的数据点在低维空间中也相互靠近。
一个SOM网络由输入层和输出层组成,输入层接收数据向量,输出层是一个由神经元组成的二维格子。每个输出层神经元都与输入层之间存在全连接的权重。在训练过程中,随机选取训练数据作为输入,计算输入向量与各个输出层神经元之间的距离,并找出距离最小的神经元,称为最佳匹配单元(Best Matching Unit, BMU)。然后根据一定的规则更新BMU及其邻域神经元的权重。这个过程反复进行,直至网络稳定。
2.1.2 SOM与其他神经网络的区别
SOM与传统的前馈神经网络相比,有以下几个显著的区别:
- 训练方式 :SOM为无监督学习,前馈神经网络通常采用有监督学习。
- 网络结构 :SOM的输出层具有固定的拓扑结构,而前馈神经网络没有。
- 学习目标 :SOM旨在寻找数据的内在结构,不直接进行预测;前馈神经网络通常用于解决回归或分类问题。
- 网络结果 :SOM的输出是数据的低维可视化表示;前馈神经网络的输出是预测结果。
2.2 Python环境下搭建SOM框架
2.2.1 安装必要的Python库
在Python环境中实现SOM,首先要安装一些必要的库。以下是常见的库以及安装方法:
-
NumPy:用于进行高效的数值计算。
bash pip install numpy -
Matplotlib:用于绘制图表。
bash pip install matplotlib -
Jupyter Notebook:用于交互式地编写和测试代码。
bash pip install jupyter -
minisom:一个轻量级的SOM库,提供了SOM的实现。bash pip install minisom
2.2.2 设计SOM网络结构的类和方法
在设计SOM网络结构时,通常会定义一个类来封装网络的属性和方法。例如,以下是一个简单的SOM类框架:
import numpy as np
from minisom import MiniSom
class SimpleSOM:
def __init__(self, x_dim, y_dim, input_len):
# 初始化SOM的尺寸和输入向量的长度
self.x_dim = x_dim
self.y_dim = y_dim
self.input_len = input_len
# 初始化MiniSom网络
self.som = MiniSom(x_dim, y_dim, input_len, sigma=1.0, learning_rate=0.5)
self.som.random_weights_init(data)
def train(self, data, num_iterations):
# 训练SOM网络
for iteration in range(num_iterations):
for x in data:
self.som.update_random(x)
def find_bmu(self, x):
# 找到最佳匹配单元
return self.som.winner(x)
# 其他必要的方法...
在这个类中, __init__ 方法初始化了SOM网络的尺寸和输入向量的长度,并创建了 MiniSom 实例。 train 方法用于训练网络,其中 num_iterations 为训练的迭代次数。 find_bmu 方法用于找到输入向量 x 的最佳匹配单元。
这个类的实现只是一个基础框架,根据实际情况,你可能需要添加更多的方法,比如网络权重更新、学习率调整、数据预处理等。
3. minisom 库安装与使用
minisom 是一个轻量级的、易于使用的Python库,用于实现Kohonen自组织映射(SOM)。本章节将介绍如何安装和使用 minisom 库,包括安装步骤、库的功能特性、创建SOM实例的参数配置、初始化SOM网络与权重等细节。
3.1 minisom 库的介绍与安装
3.1.1 minisom 的功能特性
minisom 库提供了一套完整的接口,用于创建、训练和查询SOM网络。其主要功能特性包括:
- 支持高维数据集的映射。
- 提供多种初始化和训练选项,方便用户根据需求自定义SOM网络。
- 包含了方便的数据可视化工具,例如权重可视化、热图等。
- 简洁的API接口设计,使得即使是初学者也能够快速上手。
- 支持多线程训练,加快训练过程。
3.1.2 如何安装 minisom 库
为了安装 minisom 库,推荐使用Python的包管理工具 pip 。打开命令行工具,输入以下命令进行安装:
pip install minisom
如果需要指定安装某个版本的 minisom ,可以使用如下命令:
pip install minisom==x.x.x # x.x.x代表特定版本号
如果在安装过程中遇到权限问题,可以使用 sudo (在Linux或Mac系统中)或以管理员身份运行命令提示符(在Windows系统中)。
安装完成后,可以在Python脚本中通过导入 MiniSom 类来确认 minisom 库是否安装成功。
from minisom import MiniSom
print("minisom library installed and ready to use.")
3.2 minisom 库的实例化与配置
3.2.1 创建SOM实例的参数配置
minisom 库允许用户自定义SOM网络的参数,这些参数包括网络的尺寸、学习率、邻域函数等。在创建一个SOM实例时,主要参数如下:
-
x:表示SOM网络的横向节点数。 -
y:表示SOM网络的纵向节点数。 -
input_len:输入向量的维度。 -
sigma:高斯函数的标准差,影响邻域的大小。 -
learning_rate:学习率,控制权重更新的幅度。
3.2.2 初始化SOM网络与权重
在定义了SOM网络的参数后,我们可以通过创建 MiniSom 类的实例来初始化网络和权重。以下是创建实例的代码示例:
import numpy as np
from minisom import MiniSom
# 设置SOM网络参数
x, y = 10, 10 # 网络尺寸
input_len = 10 # 输入向量长度
sigma = 1.0 # 高斯函数的标准差
learning_rate = 0.5 # 学习率
# 实例化SOM网络
som = MiniSom(x, y, input_len, sigma=sigma, learning_rate=learning_rate)
# 初始化权重,这里以随机值为例
np.random.seed(42) # 设置随机种子以保证可重复性
som.random_weights_init(np.random.uniform(-1, 1, (x, y, input_len)))
print("SOM network has been initialized with random weights.")
在上面的代码中,我们首先导入了 numpy 和 minisom 库,并定义了SOM网络的基本参数。然后创建了一个 MiniSom 类的实例,并通过 random_weights_init 方法初始化权重。权重被初始化为在-1到1之间的随机值, np.random.seed(42) 是为了确保每次运行代码时权重的初始化是相同的,以保证结果的可重复性。
初始化权重是开始使用SOM网络之前的重要一步,因为它将影响网络的学习能力和最终的聚类效果。在网络训练之前,通过随机初始化权重,可以确保网络具有初始的随机性,使得输入空间的不同区域能够在训练过程中被学习和代表。
4. 数据处理与SOM初始化
4.1 数据预处理的重要性
4.1.1 数据清洗的方法
在任何机器学习项目中,数据的质量直接影响到模型的性能。数据预处理是机器学习工作流中的重要一步,而数据清洗是预处理的首个步骤,旨在识别并修正或移除数据集中的错误和不一致性。在SOM中,数据清洗尤其重要,因为错误的数据可能导致训练出的模型无法正确地映射数据空间。
一种常见的数据清洗方法是异常值处理。异常值指的是那些与其它数据明显不一致的数据点。在SOM中,异常值可能会扭曲权重更新过程,从而影响到整个网络的学习。我们可以采用统计方法(例如箱形图)来识别异常值,并使用Z分数或IQR(四分位距)等技术来处理这些数据点。
另一种方法是缺失值处理。缺失值可能会破坏数据集的完整性。对于缺失数据,我们可以采用插值方法(如平均值插补、中位数插补或使用模型预测缺失值),或者在某些情况下,如果缺失值是随机的,我们可以选择删除包含缺失值的记录。
4.1.2 数据归一化与标准化
数据归一化和标准化是预处理步骤中确保数据在相同的尺度范围内的常用方法,这对于SOM尤其重要,因为SOM依赖于距离计算来确定数据点之间的相似性。如果数据特征的尺度相差很大,那么尺度大的特征就会对计算出的距离产生较大的影响,这可能会导致SOM网络训练不准确。
归一化通常指的是将数据缩放到[0,1]区间内,这是通过以下公式实现的: [ X_{\text{norm}} = \frac{X - X_{\text{min}}}{X_{\text{max}} - X_{\text{min}}} ] 这里( X )是原始数据,( X_{\text{min}} )和( X_{\text{max}} )分别是特征中的最小值和最大值。
标准化则是将数据缩放到均值为0,标准差为1的分布上,通过以下公式实现: [ X_{\text{std}} = \frac{X - \mu}{\sigma} ] 其中( \mu )是均值,( \sigma )是标准差。
4.2 SOM初始化策略
4.2.1 权重初始化方法
权重初始化是指为神经网络的权重设定初始值的过程。在SOM中,权重初始化尤为关键,因为它影响到网络学习的起点和收敛速度。权重初始化的基本要求是让网络的初始状态足够分散,以便网络可以探索到数据空间的不同区域。
一种常用的初始化方法是随机初始化,即权重被初始化为小的随机数。这种方法的优点是简单易行,缺点是可能会导致权重的值过小,从而使网络学习速度变慢。
另一种方法是基于数据的方法,例如使用输入数据的一部分来初始化权重。这样做的好处是能够让权重与数据本身产生联系,有助于快速学习。
4.2.2 网络结构的设置
SOM的网络结构是由一组神经元组成的二维或三维网格,每个神经元都有其对应的权重向量。网络结构的设置包括决定网格的大小和形状。网格的大小直接影响到网络能够学习到的模式的复杂度,而网格的形状可能会影响模式的表示。
通常,网格大小的选择取决于数据集的大小和复杂度,以及我们要在SOM上执行的任务。较小的网格可能无法捕捉到数据中的所有重要特征,而较大的网格可能会引入不必要的复杂度,导致训练时间增长。
网络结构还涉及到如何安排神经元的拓扑关系。在某些实现中,神经元可能被安排成一个矩形或六边形网格。这种结构的选择对于拓扑学习至关重要,因为它决定了网络在空间上保持输入数据的结构。
代码块示例
from minisom import MiniSom
import numpy as np
# 假设我们已经完成了数据预处理,并得到了归一化后的数据
# 创建一个SOM实例
som = MiniSom(x=10, y=10, input_len=100, sigma=1.0, learning_rate=0.5)
# 使用随机权重初始化
som.random_weights_init(data)
# 使用基于数据的权重初始化
som.pca_weights_init(data)
# 初始化权重(可选)
som.random_weights_init()
# 使用训练数据训练SOM
som.train_random(data, num_iteration=100)
逻辑分析和参数说明
上述代码展示了如何使用 minisom 库创建一个SOM实例并进行初始化。我们创建了一个10x10的网格,对应100个输入特征。 sigma 参数控制邻域函数的形状,而 learning_rate 控制权重更新的速度。初始化权重时, random_weights_init 方法将权重设置为小的随机值,而 pca_weights_init 方法根据输入数据的主成分分析结果来初始化权重,这有助于在权重空间中保持数据的结构。
请注意,这些代码块需要在具有正确安装的 minisom 库的环境中运行,并需要预处理后的数据集 data 可用。在实际应用中,初始化权重和训练过程可能会更加复杂,依赖于具体的应用场景。
5. SOM的训练方法
SOM的训练过程是其核心,它决定了神经网络能否学到数据的内在结构。接下来,我们将深入探讨SOM的训练方法,包括如何调整参数以及训练算法的实现步骤。
5.1 训练过程中参数的调整
5.1.1 学习率的初始化与衰减
学习率决定了在训练过程中神经元权重更新的幅度。在开始训练时,通常选择一个较大的学习率以快速找到数据的基本特征。随着训练的进行,学习率逐渐减小以精细化权重调整。
import numpy as np
# 初始化学习率
initial_learning_rate = 0.1
# 随训练进度衰减学习率
def learning_rate_decay(epoch):
return initial_learning_rate * (0.9 ** epoch)
# 假设执行300次训练迭代
for epoch in range(300):
learning_rate = learning_rate_decay(epoch)
# 执行权重更新步骤...
在上述代码中,学习率会随着训练迭代次数的增加而指数衰减。这种策略有助于模型在初始阶段快速收敛,而在之后的训练中对权重进行精细调整。
5.1.2 邻域半径的选择与变化
邻域半径定义了获胜神经元周围的邻居神经元的范围,它影响着网络在学习过程中的拓扑特性。随着训练的进行,邻域半径通常逐渐减小。
def neighborhood_radius_decay(epoch):
return maxRadius * (0.99 ** epoch)
for epoch in range(300):
radius = neighborhood_radius_decay(epoch)
# 执行权重更新步骤...
代码中的 maxRadius 是初始的邻域半径。随着训练的进行,邻域半径逐渐减小,从而使得神经元之间的竞争变得更加局部化,有助于网络学习到数据的精细结构。
5.2 训练算法的实现步骤
5.2.1 训练样本的遍历与输入
在SOM的训练过程中,训练样本需要被逐一输入到网络中,并且每个样本的输入都需要触发一次权重的更新。
# 训练数据集
training_data = np.array([...])
# 遍历每个训练样本
for data_vector in training_data:
# 找到最佳匹配单元(BMU)
bmu = find_BMU(data_vector)
# 更新权重...
这里的 find_BMU 函数用于找到与输入数据向量最匹配的神经元,即BMU。
5.2.2 权重更新规则的实现
权重更新规则根据获胜神经元和其邻居神经元来更新权重。权重更新公式通常如下:
# 假设 win_pos 是获胜神经元的位置
# neighborhood 是当前邻域内神经元的位置列表
for neuron_pos in neighborhood:
# 计算学习率和邻域函数
alpha = learning_rate * neighborhood_function(epoch, neuron_pos)
# 更新权重
som.weights[neuron_pos] += alpha * (data_vector - som.weights[neuron_pos])
在上述代码中, neighborhood_function 是根据邻域半径和迭代次数计算邻域函数值的函数。权重更新规则是SOM训练算法的核心,它确保了神经网络能够逐步学习到数据的内在结构。
SOM的训练是一个逐步迭代的过程,涉及到多个参数的动态调整和权重的更新。通过上述介绍和代码示例,可以更深入地了解SOM训练的细节,这对于IT专业人员来说是一份宝贵的资源。
6. 数据映射与节点匹配
在自组织映射(SOM)中,数据映射和节点匹配是核心步骤,通过这些步骤,数据集中的信息能够被有效地投影到一个低维的拓扑结构中。我们将详细探讨如何在SOM网络中找到最佳匹配单元(BMU)以及节点匹配和分类规则的实现。
6.1 数据向量与SOM网络的映射
数据映射是SOM神经网络的核心操作之一,其目的是将输入数据空间映射到输出层的神经元网格上,通常是一个二维网格。这个过程包括确定每个输入数据向量的最佳匹配单元(BMU)。
6.1.1 确定最佳匹配单元(BMU)
最佳匹配单元是指在SOM网络输出层中,与输入数据向量距离最近的神经元。在数学上,我们通过计算输入数据向量与每个神经元的权重向量之间的欧几里得距离或其他距离度量来确定BMU。
from minisom import MiniSom
# 假设X为输入数据集,som为已经训练好的SOM网络实例
def bmu(som, x):
bmu_location = som.winner(x)
bmu_node = som.get_weights()[bmu_location]
return bmu_location, bmu_node
# 示例数据点
data_point = X[0]
bmu_location, bmu_node = bmu(som, data_point)
print(f"BMU location: {bmu_location}, BMU node weights: {bmu_node}")
在这段代码中, winner 方法用于确定输入数据向量的BMU位置,返回的是该位置的坐标。
6.1.2 距离度量的计算方法
距离度量是SOM训练算法的关键组成部分,它决定了输入数据向量与神经元权重之间的相似度。最常用的度量方法是欧几里得距离,此外还可以使用曼哈顿距离、切比雪夫距离等。
import numpy as np
def euclidean_distance(x1, x2):
return np.sqrt(np.sum((x1 - x2)**2))
# 使用欧几里得距离计算两个向量之间的距离
distance = euclidean_distance(data_point, bmu_node)
print(f"Distance between the data point and BMU: {distance}")
这里,我们定义了一个函数 euclidean_distance 来计算两个向量之间的距离,并用它来衡量输入向量与BMU之间的距离。
6.2 节点匹配与分类规则
节点匹配是数据向量映射到SOM网络的自然结果,它涉及到节点与其邻域的匹配过程。这是理解数据聚类和可视化展示的重要步骤。
6.2.1 节点与其邻域的匹配过程
在SOM网络中,节点与其邻域的匹配是迭代进行的。通常情况下,BMU以及BMU的邻域内的神经元都会被考虑进来。节点匹配过程可以通过定义邻域函数和邻域半径来控制。
6.2.2 数据分类与聚类的实现
SOM网络的节点匹配结果可以用来对输入数据进行分类。每个节点及其邻域内的神经元代表了一类数据。这个过程与传统的聚类算法类似,但区别在于SOM使用了神经网络的方式来进行聚类。
在聚类完成后,通常会使用可视化工具展示聚类的结果,以便更好地理解数据结构和特征。可视化工具如Matplotlib可以绘制出每个聚类的代表性权重向量,以及每个数据点与邻域的关系。
通过本章的内容,我们已经深入理解了数据如何在SOM网络中进行映射,以及节点匹配与数据分类的原理。在下一章节中,我们将进一步探讨如何通过可视化工具,将SOM网络的学习结果直观地展示出来,使得我们能够更易于理解和分析数据。
简介:Kohonen自组织映射(SOM)是一种无监督学习算法,擅长于数据降维和可视化。本文详细介绍了如何使用Python及其 minisom 库来实现SOM算法,包括安装库、数据准备、初始化网络、训练过程、数据映射及结果可视化等步骤。SOM还可用于聚类分析、异常检测等,该项目中包含代码示例和数据集,有助于深入理解SOM的工作原理和实现细节。
























 1104
1104

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








